Определение погрешности наведения на стык свариваемых деталей на основе анализа закономерностей распределения плотности вероятности отсчетов координаты стыка

Характерные особенности процесса электронно-лучевой сварки - высокая концентрация энергии, малая ширина сварного шва, большое отношение глубины к ширине шва определяют повышенные требования к точности совмещения электронного луча со стыком свариваемых деталей. В настоящее время широкое распространение получили системы наведения на стык, в которых процесс обнаружения стыка и наведение луча на стык разделены во времени и проводятся в два этапа [1]. Вначале производится зондирование стыка лучом малой мощности и сохранение в памяти системы наведения обнаруженной датчиком координаты стыка. Затем мощность луча увеличивается до значений, необходимых для осуществления сварки, а перемещение луча производится по записанной ранее траектории.

Для определения достоверности записанных координат стыка перед проведением сварки их необходимо подвергнуть анализу и исключить недостоверную информацию. В основе приведенного в данной статье анализа лежит методика установления вероятностных закономерностей изменения значений координаты стыка для кольцевых стыков, исследуется форма распределения вероятности отсчетов координат стыка, устанавливается связь между коэффициентами формы распределения, энтропийным коэффициентом, средним квадратическим отклонением (СКО) и погрешностью наведения на стык.

Наиболее часто электронно-лучевая сварка осуществляется для прямолинейных, круговых и кольцевых стыков. Обычно установка свариваемых деталей в сварочном манипуляторе и их перемещение относительно оси электронно-лучевой пушки осуществляется с некоторой погрешностью, поэтому можно считать, что входное воздействие на устройство выделения сигнала от стыка в целом носит случайный характер.

Для прямолинейных стыков можно записать zст (t) = zО + vt , (1) где z- координата стыка; z0, v - случайные величины, зависящие от точности позиционирования изделия. Максимальная скорость v ухода стыка не превышает ±0,1 мм / с, величина z0 лежит в пределах ±2 мм.

Для кольцевых стыков возникает «биение»

Z ст ( t ) = Z О + Zm sin( ® t + ф ) , (2) где z ₀ , z _м , щ, ф - случайные величины, принимающие значения из следующих диапазонов: z ₀ = ±2 мм, z _м = ±2 мм, щ = 0,004...0,4 с - ¹ , ф = 0± 2п [1].

Таким образом, входное воздействие может быть описано либо линейной функцией времени, либо как гармоническое воздействие со случайными амплитудой и фазой.

Обычно для записи координаты кольцевого стыка используется один период синусоиды. Полагая, что измерения с равной вероятностью производятся в любой мо мент времени t, вероятность появления того или иного значения zсг следует считать обратно пропорциональной скорости изменения zсг в данный период времени

Р ^{( z} ст ) =

A =  Axм cos(arcsin(zст / zм))     zМ - z2

гдер(z) - плотность распределения вероятности случай ной величины z; А - нормирующий множитель;

z - максимальная величина ухода стыка.

Значение множителя А определяется из условия нормирования в пределах изменения z от - z до + z

7         .           zM

J Р(zст )dzст = Azм J / 2    2 = zм AП = 1

^z м V М ст

Отсюда

A = —(5)

z π

М и

Р(zст) =    I 21 2 .(6)

ⁿV z М ^- z ст

Такое распределение отсчетов синусоидально меняющейся во времени величины, когда моменты этих от счетов равномерно распределены во времени, называется арксинусоидальным и может быть охарактеризовано энтропийными оценками формы (рис. 1).

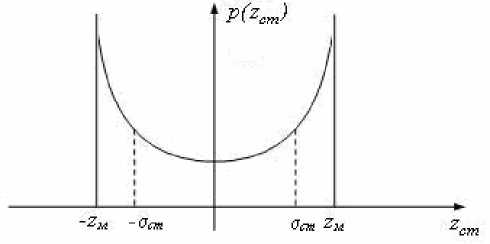
Рис. 1. Плотность распределения случайной величины z _ст; z _м - максимальная величина ухода стыка; О_ст - среднее квадратическое отклонение распределения р ( z )

Энтропия такого распределения

∞

H ⁽ z ст ) = ^- J Р ⁽ z ст ^)ln Р ⁽ z ст ) ^dz ст = ^{ln( n z} м ^/2) .    (7)

-∞

Энтропийное значение ширины плотности распределения

A (z ) =¹ H^{H ( -} °’⁾ = э х ст ^

n z M

.

Среднее квадратическое отклонение

О ст ^{( -} ст ) =      •

Энтропийный коэффициент

A (z ) к к э =       = ^ = 1,11.

О ст ( - ст ) 272

(Ю)

Выражения (6)-(10) носят характер априорных данных о процессе измерения координаты стыка. Фактичес- кое распределение плотности вероятности отсчетов координат стыка и энтропийные оценки формы могут отличаться от априорных. Это связано с тем, что в процессе зондирования стыка сканирующим электронным лучом в выходном сигнале датчика стыка возникают пульсации, вызванные неоднородностью поверхности обрабатываемого изделия, приводящие к изменению коэффициента вторичной эмиссии или рентгеновского излучения. Эти неоднородности являются следствием шероховатости поверхности, наличия забоин, царапин, химической неоднородности свариваемого материала. От помех такого рода избавиться невозможно, так как их природа заключена в физической сущности способа получения информации о положении стыка.

Результатом совместного действия этих помех является погрешность D определения координаты стыка, которая имеет среднее квадратическое отклонение О .

Учитывая, что входное воздействие z _ст , вызванное «биением» стыкового соединения, и обобщенная помеха z_n , действующая на измерительное устройство, имеют разную природу возникновения, их суммарное действие может быть найдено по правилам суммирования слабозависимых случайных величин

Оу у^ +О •             (11)

Если относительное содержание составляющей мощности помехи у„ =о„ / О, много меньше относительно- П П с!

го содержания составляющей мощности входного воздействия у _ст = О _ст / О _П , то результирующее распределение почти арксинусоидально и энтропийный коэффициент композиции k _s = 1,11.

По мере возрастания относительного содержанияу энтропийный коэффициент композиции монотонно изменяется от к^ = 1,11 до kz = 2,0. Изменение энтропийного коэффициента свидетельствует о наличии в составе управляющего воздействия погрешности, вызванной дей ствием помехи.

Проведем оценку этой погрешности. На рис. 2 приведен пример траектории для кольцевого стыка свариваемых деталей с учетом действия равномерно распределенной помехи.

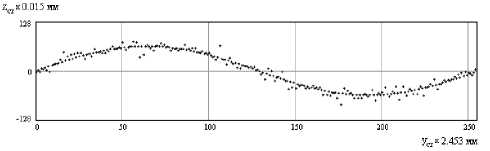
Рис. 2. Записанная траектория смещения кольцевого стыка свариваемых деталей радиусом 100 мм

На основании полученных значений z _ст . может быть построена ступенчатая гистограмма плотности вероятности отсчетов (рис. 3).

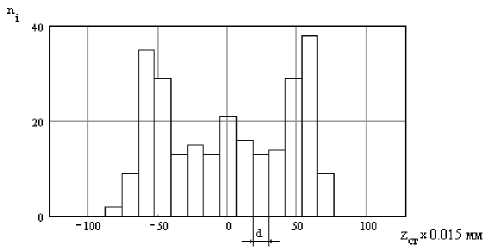
Рис. 3. Гистограмма фактического распределения, построенная по значениям отсчетов z _=т . , d - ширина столбца гистограммы

Если гистограмма состоит из т столбцов одинаковой ^шир^{ины с г}р^{аницами z} _Ст„ , ^z _иР ^z _Ст₂ , ..., ^z _cti , ^z _р ^, ^z _Ст _т ^и каждый столбец шириной d = z ₁ - z включает в себя п . результатов, то энтропия такого распределения равна Н (А) = — J р (A) in р (A) dx = — £— In — = j^,—In ^— + in d ,(12)

П    П,       П —

—то                                        —                 I                           I n где d. = z .- z . = d, p(A) = —.

-    ^{ст + 1 ст 1      P} ' nd

Энтропийное значение ширины интервала распределения будет равно ni n

А = ¹ e ^H ( ^A ) = d fr n

Э 2         2 ‘‘I n J dn io ”ы

Энтропийный коэффициент будет равен i m

Z- nig n кэ =a2, = dnio „н    ,

^О -   ^{2 0} -

.

где О _г - среднее квадратическое отклонение сохраненных координат стыка

^О -

m

Z ( - ст , — т - °’ )²

i = 1

m

= ¹ Z n i = 1

n — 1

где т,

^- С’

-стi - математическое ожидание случай ной величины z . ст

Будем учитывать то, что вычисленное по гистограм ме значение энтропийного коэффициента является энт ропийным коэффициентом композиции законов распределения входного воздействия и помехи кэ = кz (Ост, Оп ),                    (16)

а вычисленное по значениям z _ст . значение СКО О _г является результатом сложения СКО входного воздействия и СКО помехи

^О - = О 7^О 2 т ^+О П . (¹²)

Совокупность зависимостей энтропийного коэффициента кз от соотношения мощностей суммируемых составляющих для различных законов распределений может быть представлена в виде семейства графиков [2]. Эти зависимости не выражаются простыми аналитическими соотношениями, но могут быть решены численно для известных законов распределений. Результаты решения для композиции арксинусоидального с нормальным, равномерным и арксинусоидальным распределениями представлены на рис. 4, где по оси ординат отложены значения относитель-оП ного веса мощности помехи р„ = -р----у, а по оси абс-

°ст > о цисс значение энтропийного коэффициента kz, образующегося при этой композиции.

Зависимость энтропийного коэффициента компози-

^в

ции арксинусоидального и нормального распределений (кривая 1) с точностью 10 % при kz > 1,5 аппроксимируется выражением k z = 2,07 - 0,505p 6т43,

гдер - относительный вес мощности синусоидальной составляющей.

Зависимость энтропийного коэффициента композиции арксинусоидального и равномерного распределения (кривая 2) с точностью 2 % аппроксимируется выражением kz= 1,11 + 0,62 [ p п +1,34 p ^(1 - P п) ]. (19)

Обычно относительный вес мощности помехи невысокий ( р < 0,1). Это обстоятельство позволяет определить мощность помехи по значению энтропийного коэффициента композиции k _z с точностью до 5 % по любой из кривых (рис. 4), так как на участке 0 < р <0,1 эти кривые расположены достаточно плотно и почти совпадают При k _z> 1,6 можно воспользоваться аппроксимирующим выражением, полученным из (18).

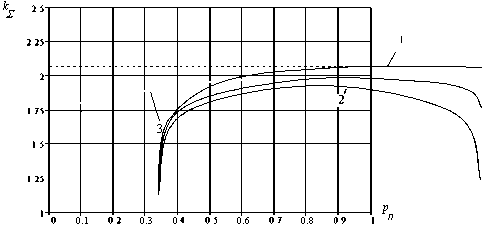
Рис. 4. Зависимость энтропийного коэффициента k _z композиции арксинусоидального распределения отсчетов координаты стыка от относительного веса_ р _л мощности помехи. 1 - помеха распределена по нормальному закону;

2 - помеха распределена по равномерному закону;

3 - помеха распределена по арксинусоидальному закону ln

2,07 - k _z Y

P _CT = ф ( k z ) = exp

Отсюда следует

^О п = /рЖ.

= o

0,505

6, 43

.

_x1 -ф ( k z ) • (21)

Погрешность наведения на стык D с доверительной вероятностью 0,9 для большой группы законов распределения помехи может быть определена как

A _n = 1,6 o _n = 1,6 о z V 1 -ф ( k z ) •

Проведем оценку погрешности наведения на стык по координатам, изображенным на рис 2. Для этой траектории получим оz - 50,76 • 0,015 мм - 0,76 мм; kz- 1,78;рст - 0,92;

Погрешность наведения на стык будет

А _п = 1,6 о _п = 1,6 о _z V 1 - P _ст = 22,9 • 0,015 мм-0,34мм.

Одним из приемов, позволяющих уменьшить погрешность определения координаты стыка, является усреднение многократных отсчетов z _ст . . Суть данного подхода заключается в том, что найденная усредненная оценка координаты их центра распределения имеет меньшую случайную погрешность, чем отдельные отсчеты, по которым она находится. Координату центра распределения отсчетов можно определить в виде среднего арифметического

n z =lyz .

ст                  ст i .

n i = 1

Среднее квадратическое отклонение рассеяния этой оценки зависит от среднего квадратического отклонения разброса усредненных отсчетов о и их числа п (при независимости отсчетов друг от друга) как о. = °>. z ст

_|

n

Таким образом, среднее квадратическое отклонение случайной погрешности убывает по сравнению со средним квадратическим отклонением самих усредняемых отсчетов в 4п раз. На этом основан принцип повышения точности в результате усреднения многократных отсчетов. Положительной стороной метода является то, что при этом одновременно уменьшаются все случайные погрешности, независимо от их происхождения и закона распределения исходных данных.

Из соотношения (24) формально следует, что увеличение числа усредненных отсчетов п позволяет неограниченно повышать точность измерений. Последнее практически невозможно, так как требует больших затрат времени. Более того, сама измеряемая величина может меняться с течением времени. Данное обстоятельство следует учитывать при оценке погрешности определения координаты стыка.

Пусть входное воздействие представляет собой медленно меняющуюся синусоидальную величину, характерную для кольцевого стыка zст = zО + zм Sin(®t) = zО

1 + m sin I---

z где m = — - относительная величина биения кольцево-z0

го стыка; Т- период «биения» стыка; z _м - максимальная величина ухода стыка.

Пусть усреднение производится за время tуср = Т/ 2, а усредненный результат соотносится с серединой участка времени усреднения (рис. 5), что соответствует моменту времени 11 и значению аргумента ф1 = 2п11 / Т. Из- менение аргумента за время усреднения tуср 2Аф - 2пt/ Т. Действительное значение zст времениt1равно zст = zо [1 + m sin(фl)].

Усредненный результат составит в момент

1 + m 2 Аф

z ст z О

ф1 +Аф

J sin( ф ) d ф .

Ф1 -Аф

Учитывая, что

1 ^Ф' Г • z х ,     sin( ф₁ )sin( Аф )

— I sm^) d ф = — '^{17 v} ’      (28)

2АФФ1 -Аф                АФ можно определить текущую погрешность, вызванную усреднением

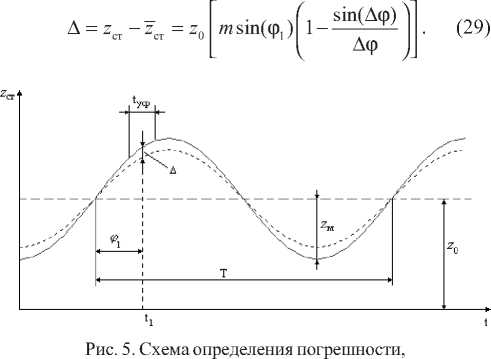
вызванной усреднением отсчетов z_ст.

Полагая, что измерения с равной вероятностью могут быть проведены в любой момент времени, вероятность появления того или иного значения погрешности D следует считать обратно пропорциональной скорости изменения D в данный период времени, т. е. распределенной по арксинусоидальному закону, и описываемой соотношением

f (А) = п V1 -А2

п с энтропийным коэффициентом Ke = 2 ^2.

Поэтому энтропийная ширина плотности распределения этой погрешности может быть определена как

^п _ ^п 2 m

^А yep ^K e ^— yep          z Од

п ³

= —z

24 ^м

t yep T

² t yep

= 1,3 z_M м

Воспользуемся разложением функции синус в ряд Тейлора

x3 x5

sin( x) = x---1+

3!5! 7!

и ограничившись двумя первыми членами ряда, полу

чим

x

sin( x ) = x 1--

или

1 _ sin( Аф ) = ( ^Аф ) ²

Аф

.

П t VCn

Отсюда следует, при Аф = t для произвольного значения t _t погрешность, вызванная усреднением, будет равна

( Аф ) 2             п ²

А = z_om -----sin( ф ) = z₀ — m

t yep

T

sin( ф )

и является синусоидальной функцией времени.

Так как заранее не известно, на какой участок траек-

тории стыка попадет отрезок времени усреднения, погрешность измерения может оказаться положительной, отрицательной или равной нулю. Таким образом, можно говорить только о вероятностях появления той или иной погрешности А и законе ее распределения.

Выражение (32) показывает, что изменение погрешности А происходит по закону

п ²

^гд^{е А} м = z О — m

t yep T

^А = ^А м ^Sin( ф ^{) , 2}

- максимальное значение по-

грешности.

Ее среднее квадратическое отклонение, как и всякой

другой синусоидальной функции t yep 1

А„    п2 m а = —м_ = z--

^{- yep}   V2   z ⁰ 6 V2

= z.

м

п ²

t yep

6л/2   T

. (34)

п ³

= —zm

24 ⁰

(t t yep

(t t yep

T

^V 7

T

V 7

.

Из проведенного анализа ясно, что при использова-

нии метода усреднения многократных отсчетов z _ст . вдоль траектории стыка погрешность результата складывается из двух частей. Первая из них

-ст

- ст =                        (37)

n монотонно убывает с увеличением затрат времени усреднения и распределена по нормальному закону, а вто

рая

п ²

° yep = z 0 "7"

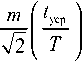
зависит от скорости изменения траектории стыка и воз

растает с увеличением времени усреднения.

Полагая, что эти два вида погрешностей взаимно независимы, для энтропийного значения их результирую

щей погрешности получаем выражение

^А" = k ^ZV °2, ⁺ - ^ ^, Р^ где к _£ - энтропийный коэффициент композиции нормального и арксинусоидального законов распределений.

Значение к в зависимости от относительного веса мощности нормальной составляющей можно определить из графика, представленного на рис. 4 (кривая 1) или аппроксими -2e рующей его формулы (18), где peT = 1 - pп = ——ycp 2 -

—- + - ст        yep относительный вес синусоидальной составляющей.

Рассмотрим пример расчета погрешности, вызванной усреднением отсчетов z . Положим, что манипулятор свариваемого изделия снабжен датчиком, который выдает 256 импульсов с интервалом времени т за полный

период вращения кольцевого стыка, а усреднение производится по 16 отсчетам z , измерение которых производится при поступлении импульса от датчика вращения. Следовательно, период обращения Т= 256т, время усреднения t = 16т.

УФ

Положим также, что характер сохраненной траектории такой, что z _м = 2 мм, а случайная составляющая погрешности отсчетов z^ имеет среднее квадратическое отклонение — _ст = 0,2 мм. В этом случае среднее квадратическое отклонение усредненных отсчетов будет равно -

— =    = 5 • 10 ^{- 2}мм .

ст n

Среднее квадратическое отклонение погрешности, вызванное усреднением, имеет значение

О уср

П 2	Z M	t У с Р	)
6	2	IT	J

= 1 • 10 ² мм.

Результирующее среднее квадратическое отклонение равно

О

=V^or+° yr = ^5,1 • ^{10 - 2 мм} .

Относительный вес синусоидальной составляющей композиции равен

Р ст

О ²

₂ ^уср ₂  = 0,04 .

° . . ⁺° уср

Этому значению, согласно графику на рис. 4 (кривая 1), соответствует энтропийный коэффициент композиции к _Е = 2,07. Энтропийное значение погрешности определения координаты стыка составит

A_z = k _zo_z = 0,1 мм.

Из вышеизложенного можно сделать ряд выводов.

• 1.    Входное воздействие на устройство контроля положения стыка носит случайный характер, при котором

• 2.    По мере возрастания относительного содержания мощности помехи распределение плотности вероятности отсчетов координат стыка меняется от низкоэнтропийного арксинусоидального с энтропийным коэффициентом к _Е = 1,11 до высокоэнтропийного с коэффициентом к ^ 2,07.

• 3.    Изменение энтропийного коэффициента в распределении плотности вероятности отсчетов координаты стыка свидетельствует о наличии в составе управляющего воздействия погрешности, вызванной действием помехи, которую можно рассчитать и уменьшить методом усреднения.

плотность вероятности отсчетов координат стыка распределена по арксинусоидальному закону