Определение порогового решения для канала с релеевскими замираниями при зондировании спектра когнитивного радио энергетическим детектором
Автор: Елисеев С.Н., Степанова Н.В.
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии радиосвязи, радиовещания и телевидения
Статья в выпуске: 1 (81) т.21, 2023 года.
Бесплатный доступ
Характеристики систем зондирования спектра и обнаружение занятости полос спектра в когнитивном радио являются одними из основных аспектов исследования. В случае, когда рассматривается система, в которой первичный пользователь меняется или присутствуют первичные пользователи нескольких типов, используют энергетический детектор. Для работы энергетического детектора основными параметрами, которые определяют вероятностные характеристики обнаружения (вероятность обнаружения пользователя, вероятность ошибки вида «ложная тревога» и вероятность ошибки вида «пропуск цели») будут зависеть от правильного определения порога решений. В данной статье просматривается аналитический подход к определению нормированного порога решений. Цель - проанализировать и определить оптимальное значение порога решений для энергетического детектора в канале с релеевскими замираниями. Рассмотрена система зондирования спектра в когнитивном радио. Определены нормированные величины порогового решения для канала с релеевскими замираниями. Представлены графические иллюстрации результатов анализа и вычислений. Полученные результаты определения пороговых решений являются хорошим приближением для расчета характеристик систем зондирования в когнитивном радио в каналах с релеевскими замираниями, обеспечивая возможность с большей вероятностью определить полосы частот, свободные от первичных пользователей, за счет чего повышается эффективность использования радиочастотного спектра.
Зондирование спектра, когнитивное радио, релеевские замирания, энергетический детектор, оптимальная величина порога
Короткий адрес: https://sciup.org/140302542
IDR: 140302542 | УДК: 543.42 | DOI: 10.18469/ikt.2023.21.1.10
Текст научной статьи Определение порогового решения для канала с релеевскими замираниями при зондировании спектра когнитивного радио энергетическим детектором
Рост запросов на беспроводные услуги за последние несколько лет иллюстрирует огромный и постоянно растущий спрос бизнес-сообщества, населения и государства. С ростом коммуникаци- онных приложений спектр становится все более перегруженным. Существующая система назначает разные полосы частот различным пользователям или поставщикам услуг, а для работы в этих полосах необходимо наличие лицензий.
Таким образом, даже если спектр может быть распределен конкретным пользователям, это не обязательно гарантирует, что он используется наиболее эффективно в любое время. Оказывается, что значительная часть радиочастотного спектра может использоваться неэффективно. Это и послужило причиной того, что нелегитимные пользователи могли использовать лицензированные полосы, предполагая, что это не вызовет никаких помех. Когнитивное радио рассматривается как новый подход, который может справиться со спектральными ограничениями. Этот подход предназначен для определения факта использования конкретного сегмента радиочастотного спектра в настоящее время и быстрого перехода к временно неиспользуемому спектру, без вмешательства в передачи других пользователей.
Описание системы зондирования спектра
Зондирование спектра (ЗС) - это ключевая про цедура в технологии когнитивного радио с динамическим доступом вторичных пользователей (ВП) к полосе частот, предназначенной для работы лицензированных первичных пользователей (ПП). Зондирование спектра позволяет обнаруживать полосы частот, свободные от сигналов, работающих ПП [1]. Сигнал для ЗС может быть записан как:
У . ( n ) =
w ( n ), npu ^ H 0
h5 ( n ) + w ( n ), npu ^ H 1
где yi ( n ) – сигнал, принимаемый i-ым ВП на интервале зондирования; 0 < n < N ; w ( n ) – сигнал помехи типа белый гауссов шум (БГШ); h. - коэффициент передачи по радиоканалу от ПП к i -му ВП; 5 ( n ) - сигнал, передаваемый ПП; H 0 - состояние радиоканала в отсутствии сигнала s ( n ); H 1 – состояние радиоканала при наличии сигнала s ( n ).
Задача ЗС состоит в следующем: по сигналу yi ( n ) на интервале длительностью N обнаружить наличие сигнала s ( n ). Таким образом, задача ЗС является двухальтернативной задачей статистической теории проверки гипотез [1]. Решение в пользу одной из двух гипотез выносится по правилу:
Y > Л решение H 1 ,
Y < Л решение H0, где Л - значение порога решения; Y — функционал, обладающий свойствами достаточной статистики, т.е. содержащий в сжатом виде всю информацию, которая имелась в сигнале y (n) об истинности гипотез H0 и H1 [2]. В случае энергетического детектора (ЭД):
N
Y =!| У .(n )| . (3)
В ряде работ рассматривался критерий оптимизации порога решения в форме суммарного значения вероятности ошибочного решения Pe :
Pe = Pm + Pfa = PY < Л / HJ + PY > Л / H0) ,(4) где Pm = 1 — Pd - вероятность ошибки вида, «пропуск цели», когда фиксируется, как истинная ги- потеза H0 , при работающем ПП;
P d = P ( Y > Л / H 1 ) - вероятность обнаружения, работающего ПП;
P fa - вероятность ошибки вида «ложная тревога», когда фиксируется, как истинная гипотеза H 1 , при отсутствующем сигнале ПП.
В работе [2] получены аналитические выражения Л0 - оптимального значения порога, которое минимизирует (4) по условию —- = 0 в канале 9Л с h = const, т.е. в канале только с аддитивным белым гауссовским шумом (АБГШ). Тогда Л0 в таком случае - функция трех аргументов N, от - дисперсии АБГШ и соответственно значение У отношения сигнал/шум (SNR) равняется:
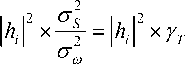
где O' S - мощность отсчета сигнала s ( n ), 2
от - мощность шумового отсчета, Ут - отношение сигнал/шум на передающей стороне радиоканала.
Л = N Ol f l ± 1 1 + 2 , (1 + (1 + ■ ' ) In (1+ ^ ) , (6)
2 IV N y 2 )
где In – натуральный логарифм.
Рассматривая каналы с замираниями, требуется в (4) переходить к Pm – средней величине вероятности «пропуск цели», являющейся математическим ожиданием Pm , полученным усреднением по распределению случайной величины У . Для рассматриваемых в работе Релеевских замираний, У имеет экспоненциальное распределение [1; 2]:
f ( У ) = -еУ / У , (7)
У где У - среднее значение SNR.
Точное выражение для
значение оп-
Л Ор -
тимального порога для усредненного значения
P e = P m + P fa (формула 9[2]), получить в компактном виде, пригодном для анализа не удается.
Альтернативный путь заключается в усреднении значений Л 0 из (6) по распределению y из (7).
Для упрощения интегрирования и получения более компактного результата учтем следующие обстоятельства:
1) случай низких значений SNR, У < 1 проана
лизирован в [2], где показано, что Pe имеет минимум около значения Л Ор ~ N ^ l ;
2) вклад слагаемого чения порога (5) для y ” 1
(1 + 2 / ) In (1 + 2 / )
ny 2
в зна-
и N=10 не превыша
ет 6,6% от точных значений Л ) , при N=50 менее
2,5%, с ростом SNR эта погрешность уменьшается.
В результате приближенное значение норма-
лизованного искомого параметра числяется следующим образом:
Л Оп =
Л Ор
N^
вы-
Лоп =1Т (Ф + 2YY )1 eY /YdY = 2 о
_ 1
a ( 4nerfc (— ^) + ^ e— ) e a
= — + — x-----------a-P----a-P,
2 22
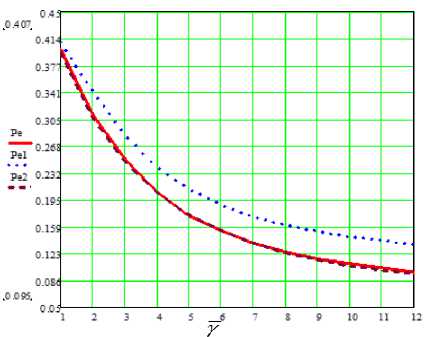
где a = y . На рисунке 1 представлен график значений по параметру Л ^р , рассчитанный по формуле (8).
чения +/-L. В нашем случае, учитывая выпуклый характер функции (8) имеем -L,+L,-L.
Процедуру определения параметров линей-но-ломанной аппроксимации (9) рассмотрим подробно на примере интервала Y
Шаг 1. Определим значения коэффициентов в уравнении хорды, пересекающей кривую (8) в точках Y =1,11.
Шаг 2. Определим А - максимальное отклонение значений функции (8) от значений вышеопре-деленной хорды на интервале Y
Шаг 3. Сдвинем по оси ординат линейную функцию (9), добавив к свободному члену Ь1 слагаемое Δ/2.
Полученная линейная функция , как можно видеть, является наилучшей линейной аппроксимацией функции (8)
У ( Y ) = к / + b + А / 2.
В соответствии с исходными данными, приведенными на рисунке 1, были определены значения коэффициентов в уравнениях (9):
к 1 = 0,089, Ь 1 = 1,147, к 2 = 0,0542, b 2 = 1,49.
Соответствующий график приведен на рисунке 1а.
Результаты
Можно убедиться, что результирующая функция (8) в диапазоне значений аргумента 1 < Y < ” является непрерывной, монотонно-возрастаю-щей выпуклой функцией, и, следовательно, в первом приближении она может быть аппроксимирована y ( / ) линейно-ломанной функцией для
Для вычисления усредненного значения вероятности ошибки р, в канале с Релеевскими замираниями воспользуемся формулами (1) и (6) (последняя получена из общей формулы замираний Накагами) из [2], а так же свойствами Q-функции:
Q ( х ) = 1 - Q ( _ л -); Q ( л ) = 2 erfc ( 22 );
Pe = 1 - exp
2 ny г
+ Л 1 - Л Оп )
X
двух интервалов Y :
У ( Y ) = к / + b для
У ( У ) = k 2 У + b 2 для
1 < y < 11
;
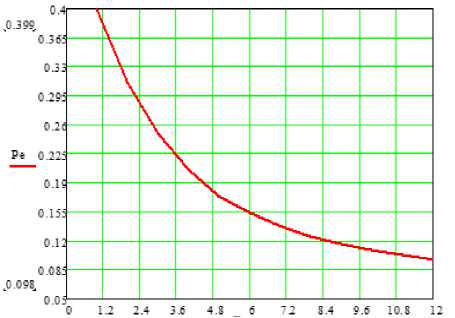
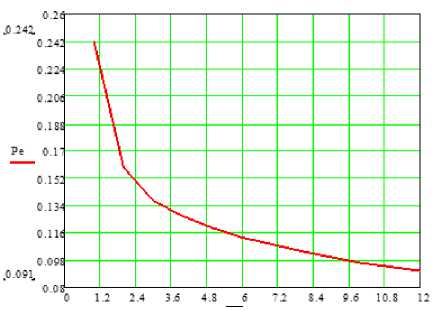
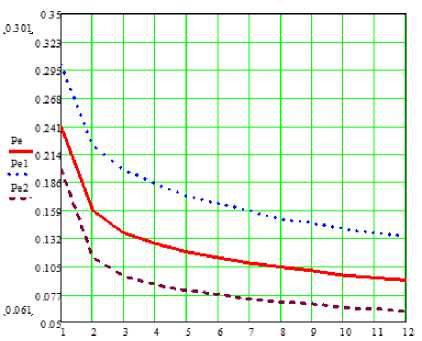
11 < y По логике определения порогового значения, естественно выбрать в (9) критерий наилучшего равномерного приближения [5]: параметры аппроксимирующей функции определяются таким образом, чтобы в интервале приближения наибольшее по абсолютной величине отклонение функции от непрерывной аппроксимирующей функции было бы минимально возможным. При этом наибольшее по абсолютной величине отклонение аппроксимирующего полинома (9) (в данном случае степени n=1) от функции (8) будет минимально возможным, если в интервале приближения – это отклонение не менее чем n+2 раза принимает свои последовательно чередующиеся предельные зна- XQ (>. (1 - Лоп)+N/ )■ Для расчета Pe берем Лоп, рассчитанный по формуле (8), сначала N=10, потом считаем при N=50. Полученные графические иллюстрации Pe приведены ниже. Из которых можно видеть, что с ростом N, уменьшается вероятность ошибки, так как при больших значениях N увеличивается точность расчетов. Порог, используемый в алгоритмах обнаружения на основе детектора энергии, зависит от величины мощности шума. Следовательно, небольшая ошибка оценки мощности шума приводит к значительным потерям производительности системы зондирования [6]. В [7] рассмотрена методология определения оценочного значения, чтобы выбрать порог, при котором будет достигнута постоянная частота ложных срабатываний. Ите- рационный алгоритм был предложен для поиска порога решения в [8]. Пороговое значение определяется итеративно для достижения указанного уровня достоверности, то есть вероятности ложных срабатываний. Прямые методы, основанные на измерениях энергии, обсуждались в [9] для неизвестных сценариев мощности сигнала. Данный метод адаптивно оценивает уровень шума. Следовательно, он подходит для практических случаев, когда дисперсия шума неизвестна. Рисунок 1. График значений по параметру λOn Рисунок 1а. График линейно-ломаной аппроксимации y(γ) Поэтому при получении формулы (7) авторы полагали величину мощности шума ст^ постоянной детерминированной величиной. В реальных условиях, по целому ряду причин [4; 5] мощность шума может быть определена с некоторой степенью неопределенности. При анализе характеристик энергетического детектора [4; 5] применяют модель ограниченной неопределенности: точное или номинальное значение ст^ лежит в ограниченном интервале: < ст^< р^т , (11) ρ где р - параметр, характеризующий степень неопределенности ст^. γ Рисунок 2. График значения вероятности ошибки в канале с Релеевскими замираниями при N=10 γ Рисунок 3. График значения вероятности ошибки в канале с Релеевскими замираниями при N=50 Распределение случайной величины ст^ подчиняется равномерному закону распределения [5]. Таким образом, значения γ в (10) должны рассматриваться в интервале γ ≤γ ≤ργ . ρ Ниже приведены графики значений вероятности ошибки в канале с Релеевскими замираниями на рисунке 4: 1) Pe при N=10; γ = 1…12; 2) Pe1 при N=10; γ = γ/ρ, где ρ= 1,5; 3) Pe 2 при N=10; Y = РУ , где Р = 1,5. На рисунке 5 приведены графики значений вероятности ошибки в канале с Релеевскими замираниями: Pe при N=50; γ= 1…12; Pe1 при N=50; γ = γ/ ρ, где ρ= 1,5; Pe 2 при N=50; У = ру, где р = 1,5. По графикам на рисунке 4 видно, что более низкая вероятность ошибки будет Pe 2 при Y = PY и Pe при Y = 1^12. Значения у них почти одинаковые, чего нельзя сказать про Pe1 . Здесь значение вероятности ошибки больше. Проанализировав следующий график, на рисунке 5, и сравнив его с первым графиком на рисунке 4, можно отметить, что при одинаковых λOp , ρ , вероятность ошибки меньше при большем значении N. Это связано с тем, что чем больше мы берем точек, тем более достоверным и точным получается результат. Также при большем значении ρ и в интервале от γ ≤ ργ вероятностная характеристика лучше. Рисунок 4. Графики значений вероятности ошибки в канале с Релеевскими замираниями, при N=10 γ Рисунок 5. Графики значений вероятности ошибки в канале с Релеевскими замираниями: при N=50 Зондирование спектра на основе детектора, требующее минимум априорных сведений о ПП, демонстрирует весьма устойчивое качество характеристик обнаружения в широком диапазоне значений SNR. Изменения в этом показателе могут быть обусловлены как ограниx`ченной точностью мониторинга свойств канала и мощности шума, так и объективной природой нестационарности ра- диоокружения [10]. Полученные в данной работе результаты позволяют прогнозировать диапазон ожидаемых характеристик обнаружения и граничные их значения в сценариях «наихудшего случая».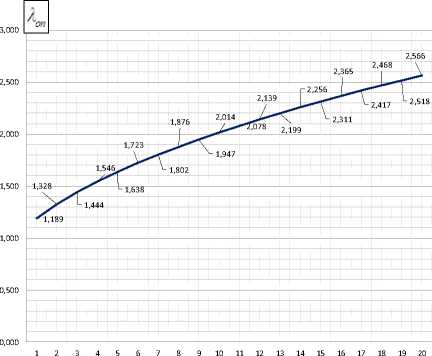
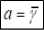
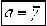
Список литературы Определение порогового решения для канала с релеевскими замираниями при зондировании спектра когнитивного радио энергетическим детектором
- Letaif K., Zhang W. Cooperative Communications for Cognitive Radio Networks // Proceeding of the IEEE. 2009. Vol. 97, no. 5. P. 878-893. EDN: MDNWTF
- Atapattu S., Tellambura Ch., Jiang H. Spectrum Sensing via Energy Detector in Low SNR // Proceeding on IEEE International Conference on Communications. 2011. DOI: 10.1109/ICC.2011.5963316 EDN: YAXLBJ
- Eliseev S.N., Stepanova N.V., Trifonova L.N. Cooperative spectrum sensing in cognitive radio networks with Rayleigh fading // Волновая электроника и инфокоммуникационные системы (WECONF-2020): материалы XXIII международной научной конференции. Санкт-Петербург, 2020. С. 224-235.
- Najafabadi Z.H. Impact of wireless channel uncertainty upon M-ary distributed detection systems // Stars library university of Central Florida, 2016. P. 1-29.
- Liu Y., Li F., Hu G. Performance Analysis of Cooperative Spectrum Sensing under Noise Uncertainty // Applied Mathematics and Information Sciences. 2012. no. 6-2S. P. 587S-593S.
- Sahai A., Hoven N., Tandra R. Some fundamental limits on cognitive radio // Allerton Conference on Communication, Control and Computing. Monticello, Illinois, 2004. P. 1-11.
- A scalable dynamic spectrum allocation system with interference mitigation for teams of spectrally agile software defined radios/ M.P. Olivieri [et al.] // IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks. Baltimore, 2005. P. 170-179.
- A framework for RF spectrum measurements and analysis/ F. Weidling [et al.] // IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks. Baltimore, 2005. Vol. 1. P. 573-576.
- Spectrum sensingwith forward methods/ J. Lehtomäki [et al.] // IEEE Military Communications Conference. Washington, 2006. P. 1-7.
- Tang H. Some physical layer issues of wide-band cognitive radio systems // IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks. Baltimore, 2005. P. 151-159.


