Определение потерь мощности и энергии на базе матрицы коэффициентов распределения в условиях векторного регулирования

Развитие электроэнергетики в современном направлении и новые отношения между субъектами производства, распределения и потребления электроэнергии требуют разработок адекватных моделей для решения различных задач, в том числе и задачи определения потерь мощности и энергии, которые должны обеспечивать качественное и эффективное управление технологическими процессами в электрической системе [1].

Наиболее перспективное направление для разработок как линейных, так и нелинейных моделей поставленной задачи открывает универсальность свойств матрицы C = C '+ j C ' коэффициентов распределения [2].

Рассмотрим моделирование режимной информации в виде вектора-функции графиков полных мощностей за некоторый дискретный интервал времени Т

• $0) = [ s v ( t ) ] = [ P v ^{(t) +} jq v ^(t) ] ,        ⁽¹⁾

где v = 1,n - число независимых узлов в схеме сети, или в виде узловых токов [3]

• j (t) =[ j v ( t ) ]= j v (t) + j (t).         (2)

Представим модель потерь на основе узловых токов в детерминированной форме J = [jv] [3], определяющую распределение комплексных токов ikv по ветвям kv схемы электрической сети по выражению ikv = ckv jv = ikv + jikv , (3) (k = 1, в; в - количество ветвей в схеме), где ikv = ckv jv ckv jv , ikv = ckv jv + ckv jv соОТвеТСтвенно действительная и мнимая составляющие вектора токораспределения в схеме электрической сети.

Матричное выражение в комплексной форме для токораспределения по ветвям электрической схемы на основе (3) имеет следующий вид:

I = i '+ jF = CJ . (4)

В развитии современных энергосберегающих технологий все более актуальной становится задача снижения потерь электроэнергии.

Действенной мерой снижения потерь электроэнергии может являться коррекция токораспреде-ления (4) соответствующим изменением режимных параметров в ветвях и узлах одновременно или только в ветвях или узлах. Допустим, используя последний подход, осуществим в матричном

Электроэнергетика

уравнении (4) корректировку вектора задающего узлового тока J путем ввода матрицы-столбца в виде произведения Y _VR E _VR , в котором Y VR = G VR ^{+ j} B VR = ^{[ g} VR_{k v} J ⁺ j ^{[ b} VR_{k v} J ^- блок матрицы узловых проводимостей Y , формируемый из проводимостей ветвей, соединяющих элементы с регулирующим эффектом с электрической схемой; E _VR – вектор-столбец ЭДС в ветвях элек-

п =

■ j"

J ''

e"

VR

e"

L VR

T

3 31 L^ 41

З 32

З 42

^в 33

З 43

З 34

З 44

где

3 11 =3 22 = [ C " ] ^T RC " + [ C ' ] RC " ;

■ J""

J »

e"

VR

E J

,

трической схемы, моделирующий режимные элементы векторного(продольно-поперечного) воздействия под нагрузкой на параметры режима ( U – вектор напряжений, δ – угол между векторами напряжений),

E = E' + jE" = [e'   1 + j [e"   1.

VR VR ^J VR L VRkv J L VRkv J

3 12 =3 21 =- [ c " ] T RC "+ [ C " f RC " ;

3 13 = 3 T1 = З 24 = 3 L = [ C ] ^T RG VR + [ C " ] ^T Rb vr ;

3 14 = 3 T = -З 23 = -3 T2 =- [ C ] T RB vr + [ c " ] T RG vr ;

^ 34 = P T = -[ G vr J^T RB vr + [ B vr ] ^{T R} G vr

Корректирующие инъекции, вызванные регулирующим эффектом (например, трансформацией

P =P = [g 1T RG + [B 1T RB .

Г³³ Г44 L VR J VR L VR J VR

в ветви k v или другими явлениями), будут иметь вид:

i VR kv = g VR kv e VR kv — b VR kv e VR kv ,       (⁵⁾

i VR kv = g VR kv e VR kv ⁺ b VR kv e VR kv .       ⁽⁶⁾

На основе метода наложения векторы-столбцы действительных и мнимых составляющих

токов (4) с учетом выражений (5), (6) представим

следующими формулами:

I ' = C ' J '- C " J " + G VR E Vr

-R F"

B VR E VR ,

I" = C ' J " + CJ '+ G VR E VR

⁺ B VR E VR .

Данный подход определения токораспределе-ния обеспечивает прозрачность в определении составляющих токов в каждой ветви схемы электрической сети, зависящих от соответствующих регулируемых режимных параметров.

Потери полной мощности в питающей сети

при известном токораспределении можно опре-

В качестве апробации предложенного подхода были выполнены исследования энергорайона, включающего более семидесяти линий и около шестидесяти узлов 110–500 кВ, сложного в эксплуатации из-за энергоемких потребителей и существенно загруженных линий 110 кВ в связи с вводом новых генерирующих мощностей. Применение устройств гибкого управления позволяет снять перегрузку по длительно допустимому току, обеспечить уровни напряжений в допустимых пределах и уменьшить общие потери активной мощности в режиме максимальных нагрузок с 19,46 до 14,62 МВт. Целесообразность ввода устройств по [1] будет зависеть от их стоимости и затрат на эксплуатацию.

При использовании модели (1) для режима средних нагрузок потери электроэнергии в схеме электрической сети можно определять по выражению

делить из выражения

AS =

*

T

diag ( Z ) I = Re ( A S ) + jIm ( A S ) = n+ jq , (9)

АЭ =

TT

- J n(t)dt = -J oO

T PF P (t)

где Z=R+ j X – матрица полных сопротивлений ветвей схемы электрической сети; Т – операция

транспонирования; п и q - потери соответственно активной и реактивной мощностей.

Составляющая потерь активной мощности из выражения (9) имеет вид

п = Re (AS ) = Re

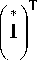
diag ( Z ) I

= Re L((I')T - j (I")T) diag (R + jX) (I'+jI") =

= ( I ' ) ^T RI " + ( I " ) ^T RI "" .

Учитывая формулы (7), (8), потери активной мощности (9) в блочно-матричном виде для схемы сети запишутся следующим образом:

1 ^T

PF ^P (t)

QF ^Q (t)

dt =

QF Q (t) _

T F P (t)

T ¹

L Q J ^{T J} L F ^Q (t)

F ^P (t) F ^Q (t)

dt . (12)

В выражении (12) B представляет матрицу формулы потерь, а множители

TT

^ Pj = 1 J f v ^p (t)f j’ (t)dt,     ^ v j = I J fv(t)f j’ (t)dt.

T0                     T0

определяются скалярными произведениями относительных графиков соответственно активных F ^P (t) и реактивных F Q (t) мощностей в узлах v и j сети, посредством которых учитывается характер изменения узловых нагрузок во времени. Для данной задачи узловые нагрузки необходимо определять при всех ожидаемых режимах внутри рассматриваемого интервала времени Т.

При краткосрочном прогнозировании узловых нагрузок использовался аппарат искусственных

Павлюков В.С., Павлюков С.В.

Определение потерь мощности и энергии на базе матрицы коэффициентов распределения… нейронных сетей (ИНС). Уточнение параметров и уменьшение погрешности проводилось решением на базе многослойной сети. В качестве активационной функции применялась сигмоида [1]

f (^ ) = 1/ (1 + e-1), где х – комбинированный сигнал для нейрона скрытого слоя.

Обучение сети проводилось с помощью алгоритма обратного распространения ошибок. Процесс начинался со случайной генерации весов многослойной сети. Во время продвижения по сети от входа к выходу рассчитываются комбинированные весовые суммы входных сигналов для текущего скрытого слоя нейронов и перевод данных сигналов к следующему слою с помощью обработки их принятой функцией активации. Для элементов выхода рассчитываются совокупные вводный и выходной сигналы. Начиная с выхода, выполняется обратное движение через нейроны скрытых слоев, предварительно вычислив значение ошибки, сравнением реальных и целевых величин исследуемых переменных на выходе. Для коррекции весов в сети на обратном ходе использовалось значение среднеквадратичной ошибки для указанных переменных. Процесс обучения носит циклический характер в виде эпох, в ходе которых минимизируется ошибка для заданной переменной или вектора переменных. После завершения обучения весовые коэффициенты фиксируются и проверяется работа сети на тестовых данных.

Рассмотренные модели (10) и (12) обеспечивают независимую от разнородности характера нагрузок узлов сети точность определения потерь мощности и энергии, что является важным фактором для получения правильных решений при выборе и использовании новых современных средств управления режимами.