Определение предельных параметров штамповки элементов трубопроводов из титанового сплава ОТ4 и стали 12Х18Н10Т

тате моделирования (рис. 2) с последующей экспериментальной проверкой и зависит от толщины заготовки и вида применяемой смазки. Приведены экспериментальные исследования и получены следующие рекомендации: для штамповки крутоизогнутых отводов принять величину зазора, равную 1,25s, где s – толщина заготовки. Принять коэффициент трения не выше 0,09. Такой коэффициент достигается применением смазки на основе машинного масла и графита с предшествующим покрытием заготовки лаком.

Для оценки разрушения изделия выполнена обработка результатов компьютерного моделирования процесса в CAD/CAE системе ANSYS/LS-DYNA.

ПРЕДЕЛЬНАЯ СТЕПЕНЬ ДЕФОРМАЦИИ ПО КРИТЕРИЮ КОЛМОГОРОВА, ПОЛУЧЕННАЯ В РЕЗУЛЬТАТЕ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ ПРОЦЕССА В ПРОГРАММНОМ ПРОДУКТЕ ANSYS/LS-DYNA

Для разработки критерия предельной степени деформации и перед экспериментальной проверкой выполнено компьютерное моделирование процесса (рис. 3). В результате моделирования определены предельные возможности формообразования для материалов: титанового сплава ОТ4 и сталь 12Х18Н10Т. Разрушения материала при штамповке рассчитано по критерию Колмогорова. Данный критерий позволяет дать количественную оценку предельной степени деформации. Моделирование выполнено в программном продукте ANSYS/LS-DYNA. Результаты моделирование представлены на рис. 3.

Метод оценки штампуемости по критерию ресурса пластичности (критерий Колмогорова) заключается в следующем: в соответствии с критерием Колмогорова образование трещин происходит при условии когда интенсивность накопленной деформации равна величине критической деформации при данной схеме напряженного состояния.

Угол гиба ф =90°

Угол гиба ф =60°

У гол гиба ф = 4 5°

Рис. 1. Отводы крутоизогнутые (ГОСТ 17375-2001)

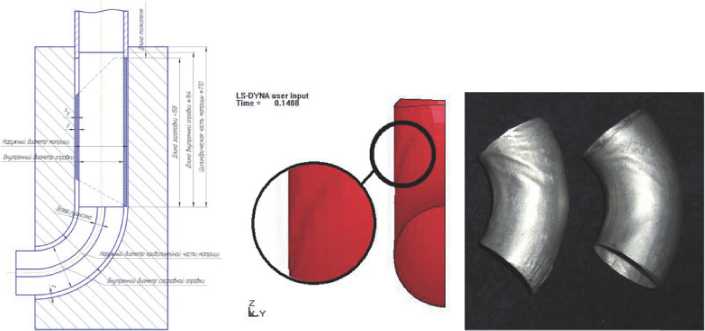
а                              б                        в

Рис. 2. Гофрообразование заготовок в процессе формоизменения при зазоре z=2,6 мм между рабочими частями штампа: а – геометрия оснастки;

б – гофры на боковой поверхности детали, полученные в результате компьютерного моделирования в ANSYS/LS-DYNA; в – гофры на боковой поверхности изделия, полученные в результате штамповки в инструментальном штампе

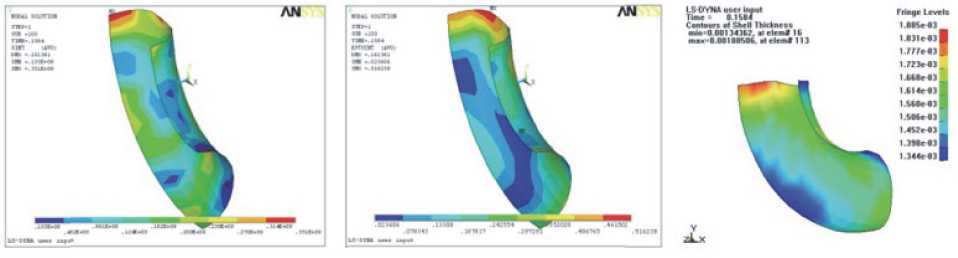
а                                   б                                   в

Рис. 3. Эпюры распределения интенсивности напряжений, деформаций и толщины на заключительной стадии процесса формообразования (угол гиба 90⁰) для материала 12Х18Н10Т: а – интенсивность напряжений, Па; б – интенсивность деформаций, %; в – распределение толщины, мм*10³

t

J d^

щ = -2--->< 1 -критерий Колмогорова;

cc

ερ при ψ ≥ 1 – происходит разрушение материала;

при ψ <  1 – разрушения не наблюдается.

Расчет критической степени деформации выполняется для узлов по максимальному и минимальному радиусу гиба по следующей зависимости:

^ С = 2 ^ ехр[ - 2.16—] -предельная сте

^{Р Р}          ^

пень деформации;

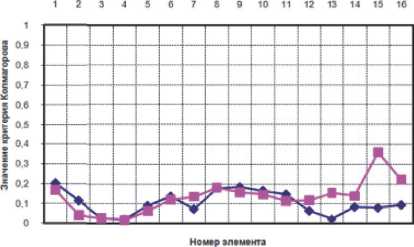
Для расчета выбирались элементы в меридиональном направлении по максимальному радиусу гиба. Результаты представлены на рис. 4 в виде графиков сравнения критерия Колмогорова для двух материалов: стали 12Х18Н10Т и сплава ОТ4 на заключительной стадии процесса формообразования (угол гиба 90 градусов).

В результате анализа полученных графиков можно сделать следующие выводы: при формообразовании отвода из стали 12Х18Н10Т разрушение не наблюдается. При этом наибольшая степень критической деформации возникает на торце передающем усилие и выходном торце по минимальному радиусу гиба. При формообразо-

Порядок замера узлов координатной сетки в меридиональном направлении

Образующая ла минимальному радиусу гида- Йлл

16 1514 13 12 11Ю 9 8 7 6 5 4 3 2 1

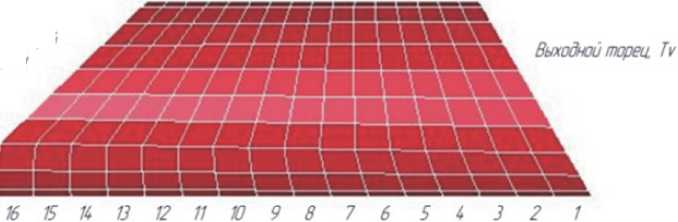
Торец передающий усилие, Ти

Образующая по минимальному радиусу гиба- ^л Распределение критической степени деформации в меридиональном направлении (по радиусу гиба)

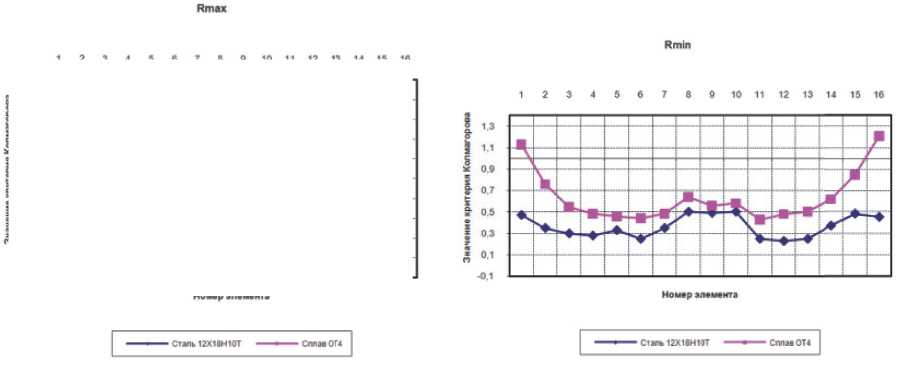
а                                     б

Рис. 4. Графики распределения критической степени деформации (по критерию Колмогорова) в меридиональном направлениях на заключительной стадии процесса формообразования (угол гиба 90 градусов) для материалов заготовки - сталь 12Х18Н10Т и сплав ОТ4: а – образующая по максимальному радиусу гиба – Rmax;

б – образующая по минимальному радиусу гиба – Rmin вании отводов из сплава ОТ4 возникает разрушение на торцах по минимальному радиусу гиба.

ВЫВОД КРИТЕРИЯ ДЛЯ ОЦЕНКИ ПРЕДЕЛЬНОЙ ДЕФОРМАЦИИ

Из анализа результатов компьютерного моделирования примем, разрушение терцев возникает в области по минимальному радиусу гиба. При этом деформация на торце ограничена углом в 60о. Параметром, препятствующему развитию очага деформации является коэффициент трения.

Для теоретического определения предельных параметров процесса формообразования примем следующие допущения:

Считаем, что элементы, получившие наибольшую деформацию растяжения, деформируются в условиях линейной схемы напряженного состояния. Такая схема имеет место на торце по минимальному радиусу гиба - Rmin;

Максимальная тангенциальная деформация возникает на открытом торце и ограничена определенным углом ( а - а ₀) (рис. 5).

Деформация торцевого сечения из круга в эллипс происходит неравномерно. Считаем, что причиной неравномерности деформации является трение на поверхности контакта заготовки с инструментом (в основном верхней оправки).

Считаем, что величина деформации E_q определяется в виде относительной величины удлинения кромки, аналогично испытаниям на растяжение.

Т.к. величина перемещения относительно небольшая, можно записать следующее уравнение деформации на торце с учетом упрочнения по линейному закону:

^д l = ^ 1°. ( exp ( f ( а — « ₀ ) ) ^- 1 ) l .

Левая часть уравнения представляет собой величину абсолютного удлинения кромки заготовки – Δl . Однако надо учесть, что увеличение длины кромки заготовки по длине окружности происходит только на небольшом участке огра- ниченным углом а.

С другой стороны, величина абсолютного удлинения кромки заготовки может быть опреде- лена в связи с принятым допущением как разница длин окружности и эллипса. Длина эллипса определяется из условия, что после деформации круглое сечение заготовки образует плоскость, проведенную через ось детали и перпендикулярную оси превращенной в эллипс, который является зеркальным отображением эллипса первоначального сечения.

С другой стороны можно определить значение l как произведение радиуса отвода на угол а . Таким образом, подставив l в уравнение и разложив показатель степени в степенной ряд exp(f а )=1+f а, можно получить уравнение для определения угла а .

Наибольшее значение а позволяет определить максимальную величину деформации Eq. Сравнив Eq с допустимой деформацией удлинения можно установить предельные возможно- сти процесса.

Таки образом, условием разрушения процесса можно принять:

E mx <  5_p , где S_p относительное удлинение образца при испытаниях на растяжение.

Для определения E mx составим систему уравнений сил действующих на элементы при оправке (рис. 5).

Проекция всех сил на ось О N :

o.F sin ^+ + Те + dof(F + dF )sin^ ^ = qF..

u i 2 u u i i 2          2 .

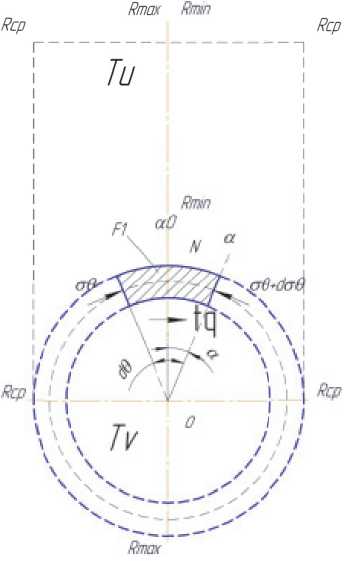
Рис. 5. Схема сил, действующий при оправке: ^ 9 - напряжения в тангенциальном направлении; F₁ , F₂ – площадь; Tu – торец передающий усилие; Tv – выходной торец;

Rmax , Rmin , R ср – максимальная, минимальная и средняя образующие соответственно

Запишем уравнения с подстановкой площадей и преобразуем:

o. q

-2- = — - уравнение Лапласа, где R₆ - ра-

Ru   s диус отвода на торце, q – сила натяжения по закону Лапласа, s – толщина отвода.

Проекция всех сил на ось, перпендикулярную О N :

T9F1 -(т9 + do9 ) f ± qf = qf2 .

Сократим уравнение с подстановкой площадей :

d O f f ± qf = qfR u d a = 0 .

Решим совместно полученные уравнения doz f = ± fda .

О

Продифференцируем полученное уравнение:

Ln o_f =± f a + C .          (1)

Постоянную С найдем из граничных условий: при а = а 0 тангенциальное напряжение равно о ₉ = o f , при этом o f = O TO + ПЕ ₆ .

С учетом того, что E _f = 0, получаем o f = o _TO . Таким образом C = Ln o f - f а ₀ .

Подставив значение С в уравнение (1), получим:

Ln °⁹- = f a + Lnof - f a₀ , преобразовав и

O9

прологарифмировав, получим:

o9 = of exp (f (a - a0)).

С учетом упрочения по линейному закону

O = On + ПЕ_Д получим: 6 TO         6 ^v

O to + ПЕ б = o f exp ( f ( a - a ₀ ) ) .

Выразим E _f :

^E6 = ° n O" ( ^exP ( ^f ( ^a - ^a 0 ) ) ^- 1 ) .    ⁽²⁾

Для определения величины E_q необходимо найти величину разницы углов ( а - а ₀ ) , определяющую область деформации.

С этой целью прологарифмируем полученное выражение (2) и разложим в степенной ряд:

E 6C, = ^<° П ( “ - ^a 0 ) ^f ,

где Е _{6 ср} - средняя деформации в тангенциальном направлении на торце.

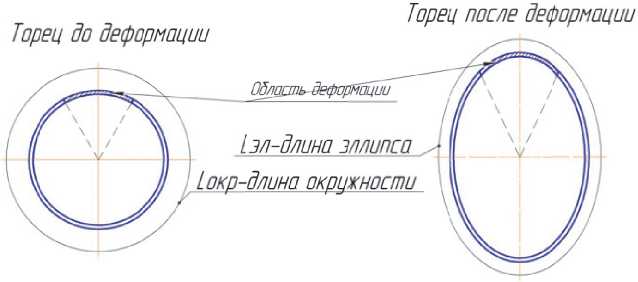
С учетом того, что средняя логарифмическая деформация в тангенциальном направлении равна отношения длин эллипса образующей от- вода к диаметру отвода (из геометрических соображений, рис. 6), получим:

E f c_P = Ln

п ( 1,5 ( a + b ) - ffi b )

2 n R_e

,

где a, b – полуоси эллипса, образованного в результате скоса торца.

Торец после деформации

Торец до деформации

Область-Зеформации кэл-длина зллипса кокр-длина окружности

Рис. 6. К определению области деформации на торце

Приравняем уравнения (3) и (4) и выразим разницу углов:

2 ^П Т

Ln

п ( 1,5 ( a + b ) - bo b )

2nR_fl и

. (5)

Подставив выражение (5) в выражение (2) получим критерий для определения предельной тангенциальной деформации на торце изделия при угле гиба 900:

E ₆ = П exp f

2 П ^ TO ^f

Ln

п ( 1,5 ( a + b ) - 4a b ) 2 n R _u

- 1

;

при E _θ ^max = E _θ ≤ δ p – разрушения не наблюдается;

при E _θ ^max = E _θ ≥ δ p – наблюдается разрешение в виде разрыва кромки.

Отметим, полученный критерий дает удовлетворительные результаты при формообразовании отводов на угол 900. Для оценки штампу-емости с меньшим углом гиба необходим анализ результатов компьютерного моделирования.

РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ

Для экспериментальной проверки полученных зависимостей определения предельных па-

раметров процесса выполнено формообразование серии заготовок с низкими пластическими характеристиками (материал ОТ4).

При этом, как показал компьютерное моделирование и теоретический расчет, разрушение наблюдается на выходном торце по минимальному радиусу гиба (рис. 7).

ВЫВОДЫ

• 1.    Выполнено моделирования процесса штамповки крутоизогнутых отводов в программном продукте ANSYS/LS-DYNA. В результате компьютерного моделирования подобраны технологические параметры, позволяющие получать изделия без гофр на боковой поверхности.

• 2.    Построены графики предельной степени деформации по критерию Колмогорова для материалов с различными пластическими характеристиками – титановый сплав ОТ4 и нержавеющая сталь 12Х18Н10Т. Установлено, отводы из титанового сплава разрушаются на выходном торце по минимальному радиусу гиба. При штамповке отводов из стали 12Х18Н10Т разрушения не наблюдается.

• 3.    Выведена аналитическая зависимость, позволяющая дать оценку критической степени деформации при штамповке отводов на угол 90⁰.

• 4.    Выполнена экспериментальная проверка подтверждающая достоверность полученных результатов исследования.

а                               б                               в

Рис. 7. Результаты экспериментальных исследований:

а – штамповая оснастка; б – изделие без разрушения и гофр на боковой поверхности; в – разрыв заготовки на выходном торце по минимальному радиусу гиба