Определение предэкспоненциального множителя в уравнении вязкости с привлечением полинома Лагранжа

Интерполяционная формула Лагранжа . Пусть f(x) есть полином степени п, который для значений а 0 , а 1 , а 2 ,... , а п аргумента х имеет соответственно значения f( а 0 ), f(a 1 ),... , f( а n ) . Согласно определению разделенных разностей, имеем [1]

f ⁽ a 0 , a 1 ,... a n , x )

__________ f ( x ) __________ +___________ f ( a 0 ) ___________ ( x - a 0 )( x - a 1 ). .. ( x - a n )   ( a 0 - x )( a 0 - a 1 ). .. ( a 0 - a n )

^{f (} a 1 ) + + ^{f (} a n )

⁽ a 1 ^- x ⁾⁽ a 1 ^- a 0 )„⁽ a 1 ^- a n )         ⁽ a n ^- x ⁾⁽ a n ^- a 0 )„ ⁽ a n ^- a n - 1 )

Так как функция f(x) есть полином степени n, ее раздельные разности порядка (n + 1) равны нулю f (30, 31, ^an,x) = 0.

Располагая множители в знаменателях приведенных выше дробей таким образом, чтобы первый множитель в каждом знаменателе был вида (х – аi), получаем

__________ f ⁽ x ) __________ =__________ ^{f (} a 0 ) __________ ( x - a ₀ )( x - a 1 ). .. ( x - a n ) ( x - a ₀ )( a ₀ - a 1 ).. ( a ₀ - a n )

f (a 1)+ +f (an)(x - a.)(a. - an)...(a. - a )        (x - a )(a - an)...(a - a .)

X 1 /X 1        0 / X 1 n /               X n /X n 0 ) X n        n -1 /

Формула (1) представляет собой интерполяционный полином Лагранжа n -й степени в виде, удобном для вычислений

Умножая обе части равенства (1) на ( x – a 0 )( a 0 – a 1 )( a 0 – a 2 )…( a 0 – a n ), можно представить его в виде

⁽ x ^- a 1 ⁾⁽ x ^- a 2 ) ■ ■ ⁽ x ^- a n )               ⁽ x ^- a 0 ⁾⁽ x ^- a 2 )■ ■ ■ ⁽ x ^- a n ) A I

J ^{( x} ) =                                      \ J ^{( a} 0 ^{) +}                                      \ J ^{( a} 1 ^{) +} .^..

⁽ a 0 ^- a 1 ⁾⁽ a 0 ^- a 2 )—⁽ a 0 ^- a n )            ⁽ a 1 ^- a 0 ⁾⁽ a 1 ^- a 2 )—⁽ a 1 ^- a n )                    (2)

+ (x - a0 )(x - a 1 )—(x - an-1 ) J(a )

...                                                                 a_n .

⁽ a n ^- a 0 ⁾⁽ a n ^- a 1 )—⁽ a n ^- a n - 1 )

Важно отметить, что когда экспериментальные данные удовлетворяют закону, который может быть выражен алгебраически в виде полинома степени п , то требуется не менее (п + l) наблюдений, чтобы составить полином. Если бы были взяты только п значений, то полученный полином был бы степени (п – 1). Поэтому, прежде чем применять формулу Лагранжа, необходимо установить, с какого порядка разделенные разности имеют постоянные значения, и таким образом найти соответствующие значения п.

Определение предэкспоненты в уравнении вязкости . В общем виде уравнение вязкости записывают следующим образом [2]

П = n 0 exp

f E}

I RT J

где Е η – свободная энергия активации вязкого течения, η 0 – предэкспонециальный множитель, который определяется путем экстраполяции кривой lgη – (1/ T ) к Т → ∞.

Принято считать, что η ₀ слабо зависит от природы жидкостей: η ₀ ≈ const. Тем не менее анализ значений η ₀ для жидкостей различной природы выше температуры плавления показывает, что величина η 0 может меняться в значительных пределах η 0 ≈ 10^-3 ÷ 10^-5 П [3, 4]. Одна из причин такого разброса может быть обусловлена экстраполяцией кривой вязкости lgη – (1/ T ) на широкий интервал, 5–8 порядков величины, от lgη ≈ 1-3 до lg η ≈ -5 (табл. 1).

Поэтому при отыскании более надежных значений η 0 необходимо привлекать известные математические методы экстраполяции.

Рассмотрим пример использования полинома Лагранжа для определения предэкспоненциального множителя в уравнении вязкости (3).

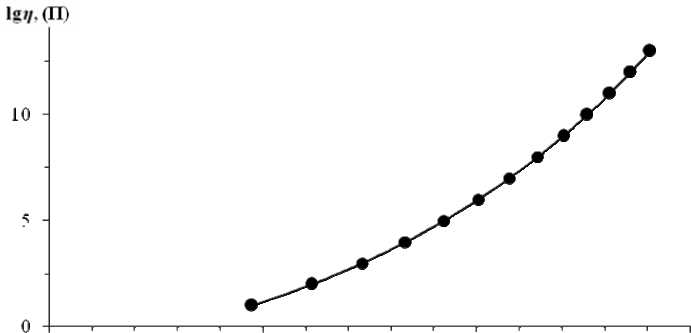
8                    10                   12              10'T.K1

Рис. 1. Температурная зависимость вязкости стекла

Построим температурную зависимость вязкости в координатах lgη – 1/Т для исследуемого стекла (рис. 1).

Таблица 1.

Экспериментальные данные вязкости натриевоборатного стекла при различных температурах [5]

Na 2 O – B 2 O 3 . Содержание Na 2 O 40 мол.%
lg η, (П)	1	2	3	4	5	6	7	8	9	10	11	12	13
105/T, K-1	9,89	10,45	10,92	11,33	11,69	12,01	12,3	12,5	12,8	13	13,2	13,4	13,6

Для определения предэкспоненты n 0 необходимо экстраполировать кривую lgn - (1/ T) в область низких температур с помощью полинома Лагранжа.

Запишем полином Лагранжа 6-й степени:

P б ( x ) = f ( a 0 )

( x - a 1 )( x - a ₂)( x - a ₃)( x - a ₄)( x - a ₅) ।

( a о - a 1 )( a о - a 2 )( a 0 - a 3 )( a 0 - a 4 )( a 0 - a 5 )

+

f ^{( a} i )

( x - a ₀)( x - a ₂)( x - a ₃)( x - a ₄)( x - a ₅)

( a 1 - a ₀)( a 1 - a ₂)( a 1 - a ₃)( a 1 - a ₄)( a 1 - a ₅)

+

+

f ^{( a} 2 )

( x - a ₀)( x - a 1 )( x - a ₃)( x - a ₄)( x - a ₅)

( a ₂ - a ₀)( a ₂ - a 1 )( a ₂ - a ₃)( a ₂ - a ₄)( a ₂ - a ₅)

+

+

f ^{( a} 3 )

( x - a ₀)( x - a 1 )( x - a ₂)( x - a ₄)( x - a ₅)

( a ₃ - a ₀)( a ₃ - a 1 )( a ₃ - a ₂)( a ₃ - a ₄)( a ₃ - a ₅)

+

+

^{f (} a 4 )

+

f ^{( a} 5 )

( x - a ₀)( x - a 1 )( x - a ₂)( x - a ₃)( x - a ₅)

( a ₄ - a ₀)( a ₄ - a 1 )( a ₄ - a ₂)( a ₄ - a ₃)( a ₄ - a ₅)

( x - a ₀)( x - a 1 )( x - a ₂)( x - a ₃)( x - a ₄)

( a ₅ - a ₀)( a ₅ - a 1 )( a ₅ - a ₂)( a ₅ - a ₃)( a ₅ - a ₄)

В нашей задаче параметр ai равен обратной величине абсолютной температуры ai = 1/Тi (i = 1, 2, 3^5), а f(ai) - логарифму вязкости f(ai) = lgni. Величина x представляет собой значение lgn при данном значении обратной температуры 1/T, которое хотим определить.

Найдем величины обратной температуры 1/ T i , соответствующие lgn i = 0, -1, -2, -3, -4, -5, -6. В качестве примеров ниже приводятся значения функции P 6 ( x ) при некоторых значениях x (см.

(4))

_ О oq (0 - 2)(0 - 3)(0 - 4)(0 - 5)(0 - 6)         (0 - 1)(0 - 3)(0 - 4)( 0 - 5)( 0 - 6) p (0 ) — 9 ,89                                             + 10 ,45                                            + (1 - 2)(1 - 3)(1 - 4)(1 - 5)(1 - 6)           (2 - 1)(2 - 3)(2 - 4)( 2 - 5)( 2 - 6) + 10 92 (0 - 1)(0 - 2)(0 - 4)(0 - 5)(0 - 6) + 11 33 (0 - 1)(0 - 2)(0 - 3)( 0 - 5)( 0 - 6) + ,     (3 - 1)(3 - 2)(3 - 4)(3 - 5)(3 - 6)       ,    (4 - 1)(4 - 2)( 4 - 3)( 4 - 5)( 4 - 6) + ц 69 (0 - 1)(0 - 2)(0 - 3)(0 - 4)(0 - 6) + 12 01 (0 - 1)(0 - 2)(0 - 3)( 0 - 4)( 0 - 5) — 9 2 ,     (5 - 1)(5 - 2)(5 - 3)(5 - 4)(5 - 6)    ",   (6 - 1)( 6 - 2)( 6 - 3)( 6 - 4)( 6 - 5)     , , qoq (1 - 2)(1 - 3)(1 - 4)(1 - 5)(1 - 6)           (1 - 1)(1 - 3)(1 - 4)(1 - 5)(1 - 6) p (1) — 9,89                                     + 10 ,45                                       + (1 - 2)(1 - 3)(1 - 4)(1 - 5)(1 - 6)         (2 - 1)(2 - 3)(2 - 4)( 2 - 5)( 2 - 6) + 10 92 (1 - 1)(1 - 2)(1 - 4)(1 - 5)(1 - 6) + 11 33 (1 - 1)(1 - 2)(1 - 3)(1 - 5)(1 - 6) + , (3 - 1)(3 - 2)(3 - 4)(3 - 5)(3 - 6)     , (4 - 1)(4 - 2)( 4 - 3)( 4 - 5)( 4 - 6)

(1 - 1)(1 - 2)(1 - 3)(1 - 4)(1 - 6) ,,       (1 - 1)(1 - 2)(1 - 3)(1 - 4)(1 - 5) _ _{о пп}

--+ 12 ,01 --------------------------------------- = 8,29 (5 - 1)( 5 - 2)( 5 - 3)( 5 - 4)( 5 - 6)          (6 - 1)( 6 - 2)( 6 - 3)( 6 - 4)( 6 - 5)

P ₍₂₎ = 9 ₈₉ (2 - 2)(2 - 3)(2 - 4)(2 - 5)(2 - 6) + 1₀ 45 (2 - 1)(2 - 3)(2 - 4)(2 - 5)(2 - 6) ¹      ,    (1 - 2)(1 - 3)(1 - 4)(1 - 5)(1 - 6)      ,   (2 - 1)(2 - 3)(2 - 4)(2 - 5)(2 - 6)

_{+ 10} 92 (2 - 1)(2 - 2)(2 - 4)(2 - 5)(2 - 6) + 11 33 (2 - 1)(2 - 2)(2 - 3)(2 - 5)(2 - 6) ,   (3 - 1)(3 - 2)(3 - 4)(3 - 5)(3 - 6)     ,   (4 - 1)(4 - 2)(4 - 3)(4 - 5)(4 - 6)

₊       (2 - 1)(2 - 2)(2 - 3)(2 - 4)(2 - 6)        (2 - 1)(2 - 2)(2 - 3)(2 - 4)(2 - 5) ₌

I ,                                                                                                                                                        1               ,                                                                                                                                                                  ,

(5 - 1)(5 - 2)(5 - 3)(5 - 4)(5 - 6)         (6 - 1)(6 - 2)(6 - 3)(6 - 4)(6 - 5)

В конечном итоге получим зависимость логарифма вязкости lgn от обратной величины абсолютной температуры для исследуемого стекла в области экстраполяции (рис. 2, табл. 2).

_________________________________________________________________________________ Табли ца 2.

Na2O - B2O3. Содержание					Na2O 40 мол.%.
lg n, (П)	1	0	-1	-2	-3	-4	-5	-6
105/T, K-1	9.89	9.21	8.29	7.04	5.26	2.71	-0.92	-6.08

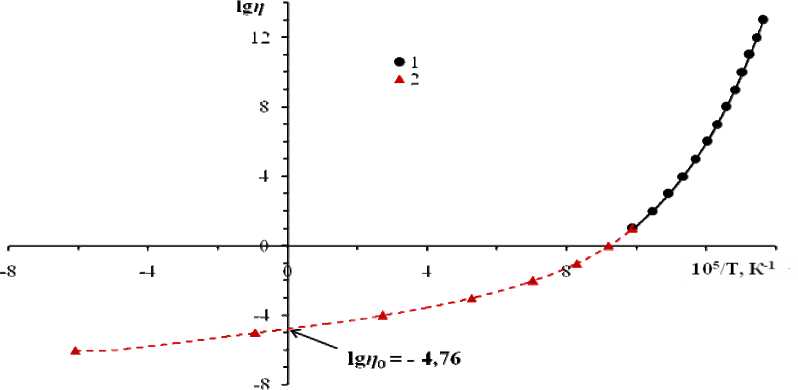
Рис. 2. Температурная зависимость вязкости в координатах lgη – 1/Т для натриевоборатного стекла. Содержание окиси натрия 40 мол.%. 1 – экспериментальные данные, 2 – расчет по методу Лагранжа

Полученная кривая (рис. 2) описывается следующим эмпирическим полиномом 6-й степени: 65432

1g n = 4 ■ 10 ¹⁸ I— I + 4 ■ 10 ¹⁵ I — I + 9 • 10 ¹¹ I — I + 2 ' 10 9 I ^r J + 3 ■ 10 5 I I + 2541 .6 I т г I - 4.7666

Значение предэкспоненты в уравнении вязкости равно: lgη ₀ = – 4,766.

Естественно, возникает вопрос “При какой степени n можно считать удовлетворительным применение полинома Лагранжа?”.

С целью выяснения этого вопроса мы провели расчеты при различных степенях n (вплоть до n = 13) в той области кривой lgη – 1/ T , где известны экспериментальные данные. При малых степенях n наблюдается заметное отклонение результатов расчета от эксперимента. Увеличивая n , доходим до значения n , при котором расчет по полиному Лагранжа совпадает с экспериментом. Отсюда вполне обоснованно можно принять, что полином Лагранжа данной степени n удовлетворительно описывает кривую lgη – 1/ T в области экстраполяции (где отсутствуют опытные данные).

Для нашего случая n = 6. Результат расчетов при n > 6 практически не отличается от случая n = 6 (рис. 2).

Таким образом, обработка экспериментальных данных по температурной зависимости вязкости стекол с привлечением полинома Лагранжа позволяет определить надежное значение предэкспоненциального множителя η 0 в уравнении вязкости.

Работа выполнена при финансовой поддержке гранта БГУ «Лучшая научная школа»