Определение прочностных характеристик базальтового композита в Comsol Multiphysics

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 552.31+676.014                                 

Использование волокнистых композитов в разных отраслях промышленности растет быстрыми темпами. По сравнению с традиционными металлическими конструкционными материалами, волокнистые композитные материалы легче и более устойчивы к коррозии, а такие качества, как прочность, жесткость, и вязкость могут быть адаптированы к конкретной области применение [1].

Волокнистый композит состоит из несущих нагрузку волокон, встроенных в расплавленный базальт, и обычно представляет собой ламинат из отдельных слоев, где волокна в каждом слое однонаправлены [6]. Для оценки упругих свойств одного слоя используется микромеханическая модель базальтового волокна в расплавленном базальте с использованием Comsol Multiphysics. Полученные параметры композита затем используются в гомогенизированном модели многослойной композитной арматуры. Для моделирования базальтового волокнистого слоистого ламината используются два подхода: послойная теория (Layerwise Theory) и эквивалентная однослойная (Equivalent Single Layer Theory) теория ; .

Определение модели в COMSOL Multiphysics

В моделировании выполняется различные типы анализов многослойной композитной арматуры. Модель разделена на три части: 1) анализ микромеханики; 2) анализ напряжений с использованием послойной теории; 3) анализ напряжений с использованием эквивалентной однослойной теории [2].

Наряду с этим, рассматривается собственные частоты и распространение поля волы напряжений в композитном материале, вычисляются прочностные характеристики композита и сравниваются с использованием обеих теорий. Собственные частоты колебаний композитных материалов и поля волны напряжений являются важной характеристикой конструкции, и определяет частоты, на которой материал колеблется в своих собственных модах. На этапе проектирования конструкции их обязательно определяют для того, чтобы либо избежать резонанса на рабочих режимах эксплуатации, либо наоборот, использовать его эффект. Кроме того, собственные частоты используются для определения состояния изделий и позволяет контролировать их качества (турбинные и компрессорные лопатки, арматуры, трубы и др. изготовленные из композитных материалов) [3].

Поскольку с течением времени в любом изделии происходят изменения геометрии и физико-механических свойств материала. Причины таких изменений могут быть разные, например, статические, динамические, температурные воздействия, коррозия, усталостное старение и др. [4].

Введение данных в параметры COMSOL Multiphysics

В данной работе для определения механических характеристик базальтового композитного материала воспользуемся пакетом прикладной программы COMSOL Multiphysics 6.0. В Таблице 1 приведены основные характеристики волокнистого композита, с учетом основных параметров моделирования и симуляции на COMSOL Multiphysics для определения прочностных характеристик композита .

В параметрах (Таблица 1) COMSOL Multiphysics вводятся данные о материалах с их описанием (Description) — с названием и описанием материалов, выражением (Expression) — с формулами, выражениями и данными для получения значении (Value), и имени (Name) — с символами, которые применяются программой COMSOL Multiphysics в процессе моделирования [5].

В определении собственных частот и формы мод, в процессе распространения волны напряжения, определяющую роль играют три параметра: это Fiber-basalt volume fraction — объемная доля волокнистого базальта, Fiber-basalt density — плотность волокнистого базальта, и Basalt density — плотность расплавленного базальта. На Рисунке 1 показано геометрия элементарной ячейки, состоящая из базальтового композитного волокна, и расплава.

Таблица 1

ПАРАМЕТРЫ COMSOL MULTIPHYSICS

Name 1	Expression 2[mm]	Value 0.002 m	Description Unit cell length
V	1'3	SE-9 mE	Unit cell volume
v_f	50	50	Fib er-ba salt volume fraction
V_f	v_f*V	4E-7m =	Fiber-basalt volume
r_f	sqrt(V_f/(pi*l))	0.007973S m	Fiber-basalt radius
E1_f	60[GPa]	6E10Pa	Fiber-basalt Young's modulus, 11 direction
E2_f	7[GPa]	7E9 Pa	Fiber-basalt Young's modulus, 22 direction
G12_f	3.46[GPa]	3.46E9 Pa	Fiber-basalt shear modulus, 12 direction
G23_f	2.75[GPa]	2.75E9 Pa	Fiber-basalt shear modulus, 23 direction
nu12_f	0.25	0.25	Fiber-basalt Poisson's ratio, 12 direction
nu23_f	0.07	0.07	Fiber-basalt Poisson's ratio, 23 direction
E_r	5[GPa]	5E9 Pa	Basalt Young's modulus
n и_г	0.35	0.35	Basalt Poisson's ratio
rho_f	2670[kg/mA3]	2670 kg/mJ	Fiber-basalt density
rho_r	2520[kg/mA3]	2520 kg/m*	Basalt density
rho_l	rh o_f*v_f + rh o_r* (1 - v_f)	10020 kg/m1	Composite basalt lamina density
th	2[mm]	0.002 m	Coniposite basalt laniina thickness
ГС	25[mm]	0.025 m	Fittings radius
he	12[mm]	0.012 m	Fittings height
Ftat	1000[N]	1000 N	Total load

Select Physics

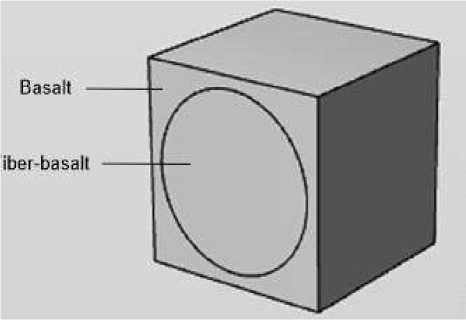
Рисунок 1. Геометрия элементарной ячейки с базальтовым волокном в расплавленном базальте

Search

• 0    ||| Heat Transfer

• >    Ф Optics

• >    © Plasma

• >    § Radio Frequency

• > ^ Semiconductor

^ ^ Structural Mechanics

^ Solid Mechanics (solid)

• □ Shell (shell)

• ^ Layered Shell (Ishell)

Q Membrane (mbrn)

Beam (beam)

J^k Truss (truss)

Ф Multibody Dynamics (mbd)

Lumped Mechanical System (Ims)

• > Rotordynamics

Рисунок 2. Окно Select Physics - Выбор раздела физики, Structural Mechanics (solid) -Структурная механика (твердое тело), Solid Mechanics (solid) – Механика твердого тела

Композитный слой изготовлен из базальтовых волокон, однонаправленно внедренных в расплавленный базальт. Элементарная ячейка из расплавленного базальта, имеющая кубическую форму в середине которой расположен цилиндр с базальтовым волокном внутри. Чтобы выполнить микромеханический анализ в узле периодичности ячейки, используется интерфейс программы COMSOL Multiphysics, Механика твердого тела (Solid Mechanics) (Рисунок 2).

При анализе микромеханики, для оценки матрицы упругости используются шесть вариантов нагружения. Распределение эффективного напряжения (по Мизесу) для четырех случаев нагрузки показано на Рисунке 3 (а, б, в, г). Из Рисунка 3 а, б, в, г, можно отметить появление напряжения в четырех случаях нагрузки в элементарной ячейке из расплава и базальтового волокна. Напряжение появляется внутри цилиндрической композитной арматуры из базальтового волокна, и распространяется сначала по бокам и сторонам ячейки. Можно заметить соответствующую деформацию сторон элементарной ячейки на фоне нагрузки.

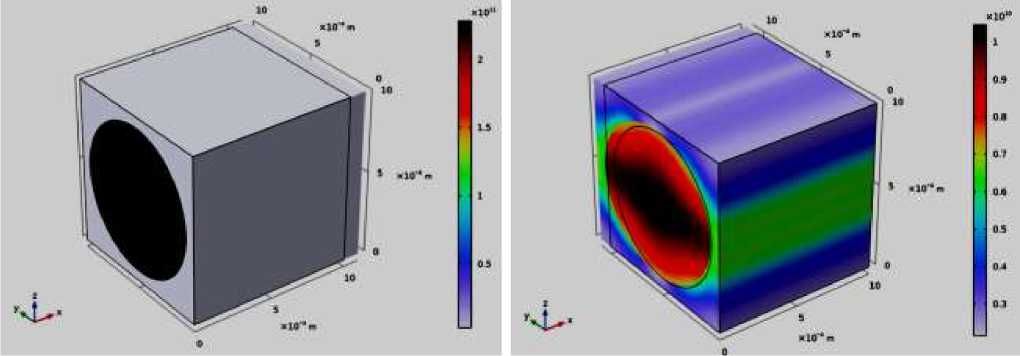
а)

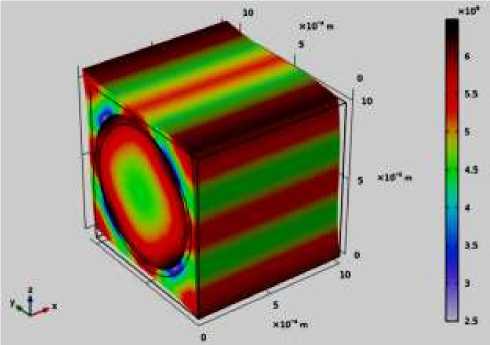
в)

Рисунок 3. а, б, в, г. Распространения напряжения по элементарной ячейке из волокнистого и расплавленного базальта

б)

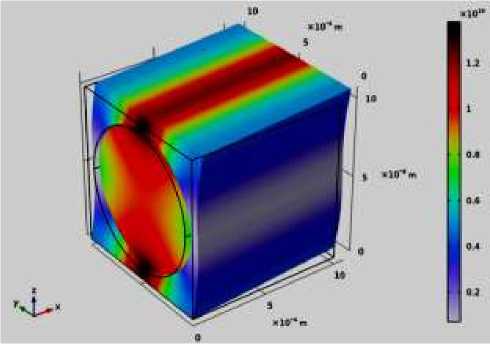
г)

Предполагается, что базальтовое волокно поперечно изотропно (моделируется как ортотропное), а расплавленный базальт считается изотропной. Свойства материала базальтового волокна и расплавленного базальта приведены в Таблице 2 и 3.

Таблица 2

СВОЙСТВА БАЗАЛЬТОВОГО ВОЛОКНА

Свойства материала	Значение
{E 1 , E 2 , E 3 }	{230, 15, 15} GPa
{G12, G23, G13}	{15, 7, 15} GPa
{υ 12 , υ 23 , υ 13 }	{0.2, 0.07, 0.2}
ρ	2670 kg/m3

Таблица 3

СВОЙСТВА РАСПЛАВЛЕННОГО БАЗАЛЬТА

Свойства материала	Значение
E	4 GPa
υ	0.35
ρ	2520 kg/m3

Последовательность укладки базальтового композитного ламината и свойства материала

Базальтовый композитный ламинат состоит из пяти слоев, толщиной 1 мм. Ориентация слоев различна. Ориентация, начиная с нижней части ламината, принимается равной 0, 45, 90, -45 и 0 градусам, как показано на Рисунке 4.

Свойства слоистого композитного материала для каждого слоя задаются как композит, в котором волокна имеют одинаковый размер и распределены равномерно в тонком слое. Первое основное направление материала, показывающее ориентацию волокон в каждом слое физической геометрии, показано на Рисунке 4.

На Рисунке 5. показан вид цилиндрической арматуры из базальтового волокна с изображением направление волокон, встроенных в расплав базальта.

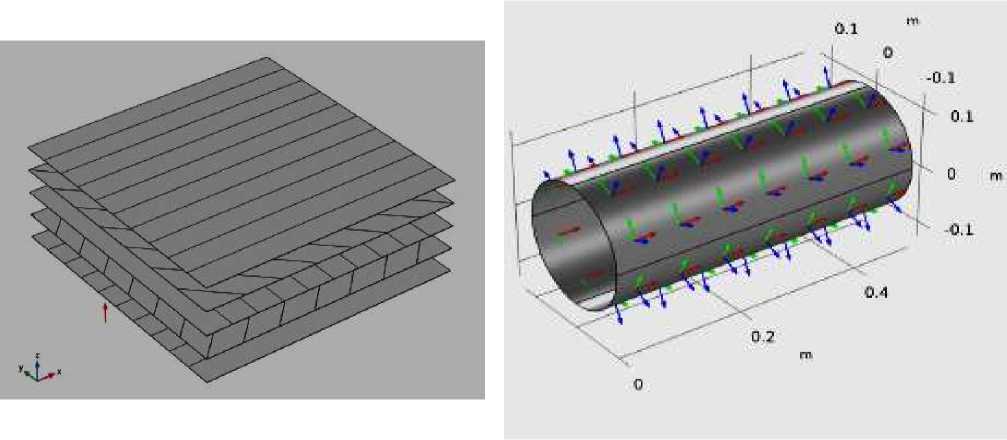
Рисунок 5. Система координат базальтового композита, показывающая первое главное направление вдоль оси цилиндрической арматуры

Рисунок 4. Последовательность укладки [0/45/90/-45/0] для ламината, показывающего ориентацию волокон каждого слоя снизу-вверх

На Рисунке 6 показан цилиндр арматуры в пяти слоях базальтового композита.

Распределение напряжений по фон Мизесу

Распределение напряжений по фон Мизесу в композитной цилиндрической арматуре, полученное на основе двух теорий (1. Эквивалентная однослойная теория, 2. Многослойная теория), представлено на Рисунке 7. Обе теории дают сходные результаты. Можно заметить, что распределение напряжений между слоями волокнистого цилиндрического композита является прерывистым, обе теории дают сходные распределения.

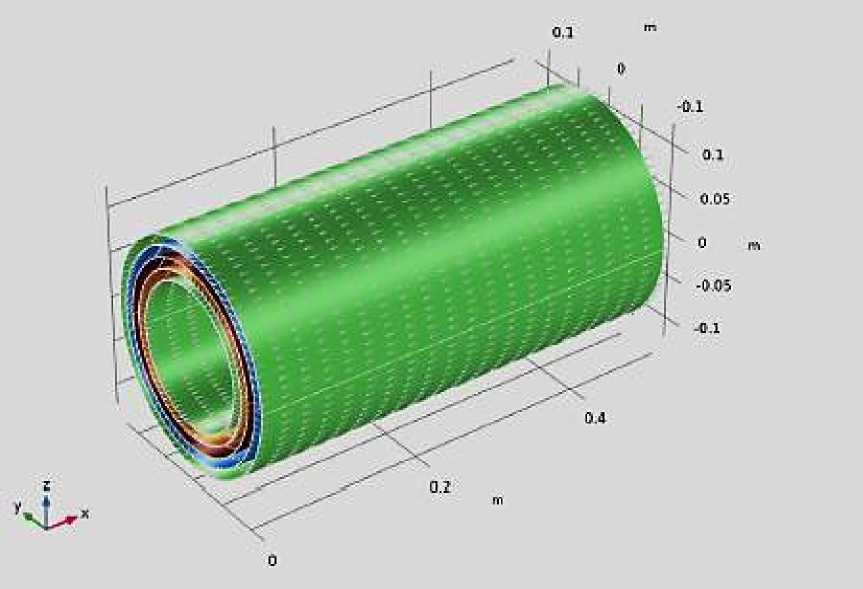
Рисунок 6. Первое основное направление материала, показывающее ориентацию волокон в каждом слое композита. Угол слоя используется в качестве цвета для каждого слоя

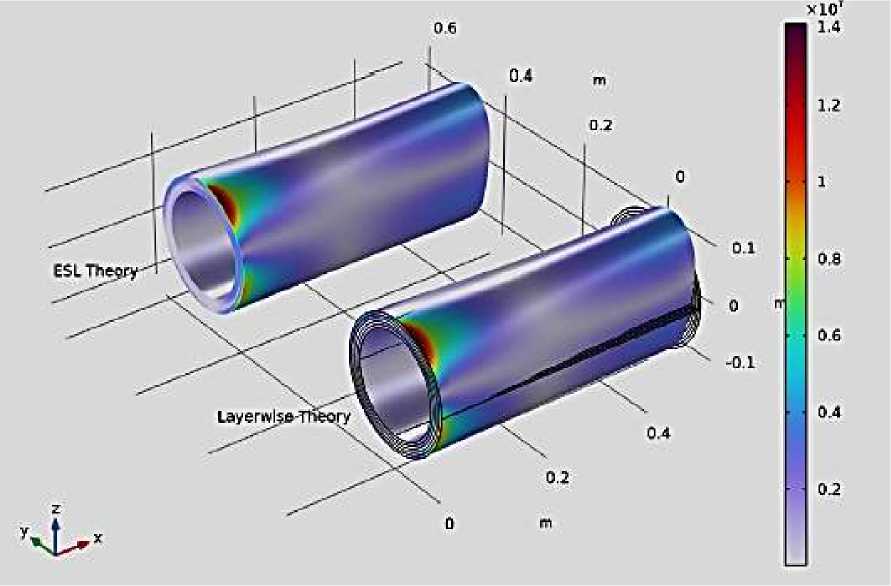
Рисунок 7. Распределение напряжений по фон Мизесу в композитном цилиндре арматуры, полученное с использованием многослойной (Layerwise Theory), и однослойной эквивалентной теориях (Equivalent Single Theory).

На Рисунке 7 отображено распределение напряжений по фон Мизесу в композитном цилиндре арматуры. Можно отметить одинаковое распределение напряжения и одинаковую деформацию в обоих цилиндрах арматуры.

На Рисунке 8 отображено второе напряжение Пиолы-Кирхгофа в многослойной системе координат, где графика составлена по координатам толщины (Thickness coordinate), и напряжения по толщине (Slm11 MPa). Прямыми, сплошными линиями обозначены многослойная теория (Layerwise Theory), а линиями, со штрихами обозначены – эквивалентная однослойная теория (Equivalent Single Theory). Как видно из графика, по координатам толщины, и напряжения по толщине, отличие распределение напряжения на многослойный и эквивалентный однослойный базальтовый ламинат невелика.

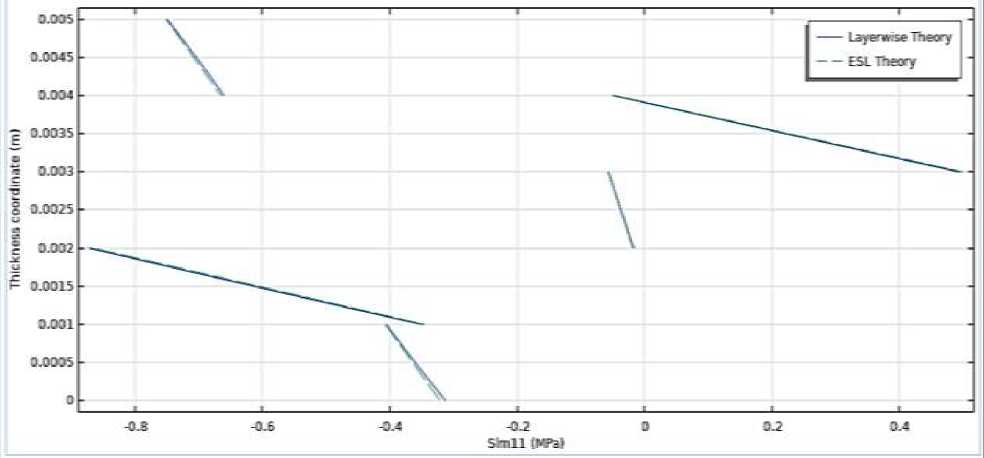
Рисунок 8. Второе напряжение Пиолы-Кирхгофа

На Рисунке 9 отображены распределение напряжений фон Мизеса в каждом слое базальтового композитного ламината с использованием послойной теории. Распределение волны напряжений в отдельных слоях заметно отличается: средний слой с волокнами, перпендикулярными первому основному направлению базальтового композитного материала имеет наименьшие напряжения. Согласно данным, представленным на Рисунке 8 и 9 можно утверждать, что отличие волны напряжений на многослойный и эквивалентный однослойный базальтовый ламинат составляет порядка 0.2%.

Первые три собственные частоты цилиндрической арматуры показаны в Таблице 4, а соответствующие формы колебании показаны на Рисунке 10.

Срез слоистого материала: напряжение по фон Мизесу (N/m2)

Таблица 4

СРАВНЕНИЕ СОБСТВЕННЫХ ЧАСТОТ

Собственная частота. Многослойная теория (Hz)	Собственная частота. Эквивалентная однослойная теория. (Hz)
486	485
573	572
984	984

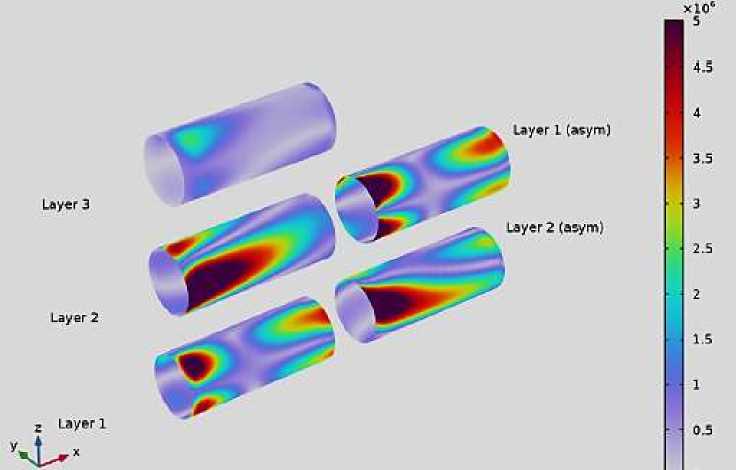
Рисунок 9. Распределение напряжений по фон Мизесу в пяти слоях ламината

Распределение поля волны напряжения в цилиндрическом базальтовом композите на различных частотах представлены на Рисунке 10.

Из Рисунка 10 видно, когда собственная частота колебаний базальтового цилиндрического композита частота составляет порядка 486 Гц, режим распространения волны напряжения внутри композита в основном представляет собой плоскую волну. С увеличением частоты внутри композита до 573 Гц появляется неплоские волны.

На основании полученных данных были сделаны следующие выводы:

• 1.    Изучены распределения поля волны напряжения трех различных значений собственных частот и формы мод в трех образцах объектов из расплава базальта и базальтового волокна с использованием пакета прикладных программ Comsol Multiphysics в элементарной ячейке с цилиндрической формы в виде композита, имеющиеся волокна внутри и расплава базальта снаружи, ламинат(плоский композит) базальтовый в пяти слоях и цилиндрическая арматура из базальтового волокна;

• 2.    Проведен анализ микромеханики композитной цилиндрической арматуры на основе многослойной и эквивалентной однослойной теории и показано, что напряжение в композитной цилиндрической арматуре, найденная на основе двух теорий отличается на 0.2%.

• 3.    Установлено, что на собственную частоту волны напряжения и форму мод в основном влияют три параметра базальтового волокна и расплава базальта: Fiber-basalt volume fraction — объемная доля базальтового волокна, Fiber-basalt density — плотность базальтового волокна, и Basalt density — плотность расплава базальта. С увеличением концентрации этих трех параметров, уменьшается собственная частота колебаний волны напряжений и соответственно меняется величина смещения в композитной арматуре.

Отсюда можно утверждать, что концентрация трех параметров расплава базальта и базальтового волокна от одного до пяти слоев арматуры влияют на прочность композитного материала.

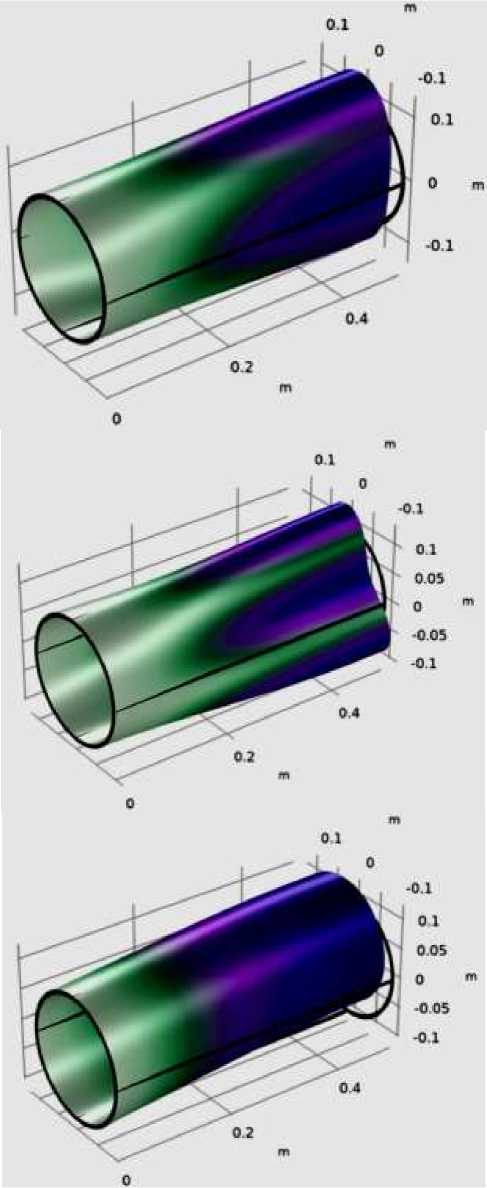
Рисунок 10. Формы колебаний и величины смещения

Собственная частота 486.03 Hz Величина смещения (м)

Собственная частота 573 Hz Величина смещения (м)

Собственная частота 984 Hz Величина смещения (м)

Список литература:

• 1.    Кобелев А. Г. Материаловедение. Технология композиционных материалов. М.: КноРус, 2016. 268 с.

• 2.    Шакирзянов Р. А., Шакирзянов Ф. Р. Динамика и устойчивость сооружений. Казань : Казанский гос. архитектурно-строит. ун-т, 2013. 119 с.

• 3.    Лаврович Н. И. Контроль усталостной повреждаемости материалов // Омский

  научный вестник. 2000. №10. С. 51-53.

• 4.    Дубко А. Н. Обобщенное решение задачи об определении частот собственных поперечных колебаний однородных прямых стержней // Вестник машиностроения. 1983. №6. С. 37-38.

• 5.    Персиков Э. С. Вязкость магматических расплавов. М.: Наука, 1984. 160 с.

• 6.    Ташполотов Ы., Маматов Э. Химический состав базальтовых горных пород Кызыл-Кийского месторождения Кыргызской Республики // Вестник Ошского государственного университета. Математика. Физика. Техника. 2022.    №1. C. 81-91.