Определение рациональной структуры разнородной системы дистанционного зондирования Земли на этапе внешнего проектирования

Автор: Волков В.Ф., Пономарев А.С., Жидков Е.Н., Толмачев А.А.

Журнал: Журнал Сибирского федерального университета. Серия: Техника и технологии @technologies-sfu

Статья в выпуске: 7 т.11, 2018 года.

Бесплатный доступ

В работе предложена методика обоснования рациональной структуры разнородной системы дистанционного зондирования Земли (ДЗЗ), позволяющая в прямой постановке для конкретных условий определять соотношение космических, пилотируемых и беспилотных средств ДЗЗ для обеспечения требуемой оперативности и качества мероприятий ДЗЗ при ограничениях на ресурсоемкость.

Дистанционное зондирование земли, эффективность, оперативность, жизненный цикл, матрица предпочтений, беспилотный летательный аппарат

Короткий адрес: https://sciup.org/146279547

IDR: 146279547 | DOI: 10.17516/1999-494X-0094

Текст научной статьи Определение рациональной структуры разнородной системы дистанционного зондирования Земли на этапе внешнего проектирования

вать процесс логических рассуждений проектировщика системы, учесть внешние факторы и установить отношения между ними.

Применение метода анализа иерархий для решения задачи обоснования рациональной структуры разнородной системы ДЗЗ

На первом шаге применения МАИ составляются матрицы приоритетов и попарных сравнений. Данные, включенные во все матрицы попарных сравнений, обрабатываются по формулам линейной алгебры в соответствии с алгоритмом, представленным в табл. 1 (исходная матрица помещена в левую часть таблицы).

Приоритеты синтезируются начиная со второго уровня вниз. Порядок синтеза состоит в следующем. Локальные приоритеты перемножаются на приоритеты соответствующего фактора на вышестоящем уровне и суммируются по каждому элементу в соответствии с факторами, на которые воздействует этот элемент.

Глобальные приоритеты позволяют путем сравнения принять окончательное решение.

Для выполнения условий согласованности в матрицах попарных сравнений используются об- ратные величины а„ = — вместо традиционно используемых при построении интервальных ij aij шкал величин ajj = — ajj. Для контроля расчетов необходимо определять индекс согласованности (ИС), который может быть получен следующим образом. Сначала суммируется каждый столбец суждений, затем сумма первого столбца умножается на величину первой компоненты нормализованного вектора приоритетов, сумма второго столбца умножается на величину первой компоненты нормализованного вектора приоритетов, сумма второго столбца на вторую компоненту и т.д. Затем полученные числа суммируются. Таким способом можно получить

Таблица 1. Алгоритм проведения расчетов

Table 1. The algorithm of calculations

A 1	1 1 _... 1 1 ωω ω ω	→	1 3 ^{1 1} ... ^{1 1} 1 2 12 13	= а ⁺	a = % 1 сумма
A 2	ω 2 ω 2_... ω 2 ω 2 ^ω1 ^ω2 ^ω12 ^ω13	^→	1 ωω ω ω ₁ ₃ 2 2 ... 2 2 ω 1 ω 2 ω 12 ω 13	= b ⁺	b - x сумма
	^…	^…	^…	^…	^…
A 12	ω ω ^... ω ω 1 2 12 13	→	ω 12 ω 12 ω 12 ω 12 13 ... ωω ωω 1 2 12 13	= n p +	^p ^- ^x 12 сумма
A 13	^ω13^ω13_...^ω13^ω13 ω 1 ω 2^... ω 12 ω 13	^→	ω 13 ω 13 ω 13 ω 13 13 ... ω 1 ω 2 ω 12 ω 13	= q + ⁺	^q ^X 13 сумма
				сум м а	—

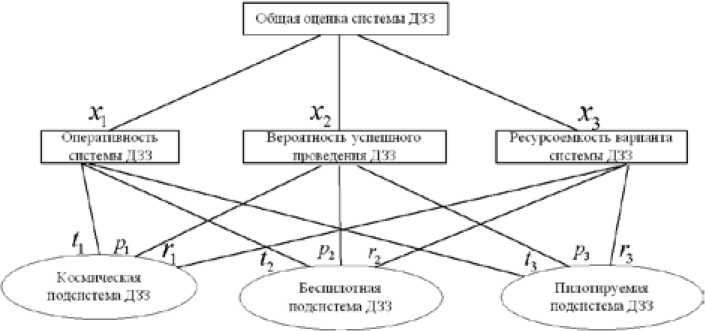
Рис. 1. Иерархия приоритетов

Fig. 1. Hierarchy of priorities величину Xmax. Для индекса согласованности имеем: ИС = (Xmax - n)/(n - 1). Для обратносимметричной матрицы всегда Xmax > n.

При реализации данного метода анализировались три типа зондирующих средств, входящих в качестве подсистем в проектируемую систему ДЗЗ: космическая (КС), авиационная пилотируемая (АВ) и авиационная беспилотная (БПЛА). Для составления «матрицы предпочтений» использовались данные экспертного опроса специалистов в области ДЗЗ. В опросе принимали участие 36 экспертов. Для оценивания достоверности полученных экспертных оценок был рассчитан коэффициент конкордации, его величина составляет 0,75.

Далее были сформированы матрицы попарных сравнений частных показателей эффективности системы ДЗЗ, а именно оперативности, результативности и ресурсоемкости для различных вариантов разнородной системы. На рис. 1 представлена иерархия приоритетов перечисленных показателей, которые обозначены через x 1 , x ₂ и x ₃ соответственно. Частные показатели оперативности, результативности и ресурсоемкости для каждой из подсистем обозначены буквами t , p и r соответственно.

Из вышеизложенного следует, что для получения общей оценки каждой подсистемы ДЗЗ необходимо умножить вес оценки этой шкалы по некоторому критерию на вес этого критерия и сложить значения, полученные для каждой системы по всем критериям. Общая оценка космической подсистемы вычисляется по формуле k = 1 1 * x 1 + p 1 * x ₂ + r 1 * x ₃, общая оценка авиационной подсистемы на базе БПЛА - b = 1 ₂* x 1 + p ₂* x ₂ + r ₂* x ₃ и общая оценка авиационной подсистемы на базе пилотируемых ЛА - a = 1 ₃* x 1 + p ₃* x ₂ + r ₃* x ₃.

Значение интегральной оценки всей разнородной системы ДЗЗ получается путем перемножения соответствующих матриц и транспонированных векторов-строк. При проведении исследований использовался генератор вариантов (комбинаций состава разнородной системы), описанный в работах [6, 7]. При этом было введено ограничение «сверху» на число вариантов, полученное из экономических соображений. Всего были рассмотрены 17 комбинаций, 4 из которых были отброшены перед принятием окончательного решения как не представляющие интереса («нулевые» варианты).

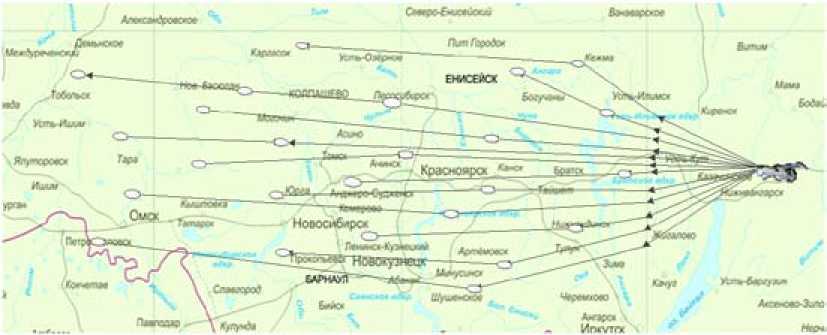
Рис. 2. Район ведения детального ДЗЗ

Fig. 2. Area of detailed RSE

Таблица 2. Исходные данные о подсистемах ДЗЗ

Table 2. Initial data on RSE subsystems

	Оперативность, мин.	Результативность	Ресурсоемкость, у.е.
Космическая подсистема ДЗЗ	15 – 45	0,95	973
Пилотируемая подсистема ДЗЗ	110 – 120	0,6	214
Беспилотная подсистема ДЗЗ	70 – 80	0,75	92

В качестве района ДЗЗ рассматривался один из регионов с размерами 100 км × 300 км (рис. 2).

Исходные данные для подсистем ДЗЗ по характеристикам оперативности функционирования, результативности (вероятности успешного проведения ДЗЗ) и ресурсоемкости (стоимости) приведены в табл. 2. Характеристики оперативности каждой из подсистем ДЗЗ заданы с учетом интервала времени на выход в район ДЗЗ (рис. 2) (для ОГ КА) и на подготовку к проведению ДЗЗ (для авиационных комплексов).

Матрица приоритетов различных показателей эффективности, сформированная экспертами, и результаты расчета вектора приоритетов представлены в табл. 3.

Исходные данные для реализации МАИ и анализ результатов расчетов

В табл. 4-6 представлены результаты расчетов векторов приоритетов по каждому показателю (оперативности, результативности, ресурсоемкости) для разных вариантов состава разнородной системы. Результаты расчетов интегрального показателя для каждого варианта отражены в табл. 7, на рис. 3 приведена соответствующая графическая зависимость интегрального показателя от номера варианта состава системы.

Table 3. Matrix of priorities of indicators of efficiency, effectiveness, resource intensity of the RSE system

	Оперативность	Результативность	Ресурсоемкость	Вектор
Оперативность	1	0,33	0,75	0,181378
Результативность	3	1	3	0,598898
Ресурсоемкость	1,33	0,33	1	0,219724

Таблица 4. Матрица попарных сравнений по показателю оперативности для различных вариантов состава разнородной системы ДЗЗ

Table 4. Matrix of pairwise comparisons in terms of efficiency for different variants of the heterogeneous RSE system

k: a: b	2: 4: 2	2: 3: 4	2: 2: 6	2: 1: 8	1: 9: 2	1: 8: 4	1: 7: 6
2: 4: 2	1,000	0,900	0,800	1,500	0,670	0,700	1,200
2: 3: 4	1,111	1,000	0,900	1,500	0,670	1,000	1,200
2: 2: 6	1,250	1,111	1,000	1,500	0,670	1,000	1,200
2: 1: 8	0,667	0,667	0,667	1,000	0,440	0,670	0,800
1: 9: 2	1,493	1,493	1,493	2,273	1,000	1,500	1,800
1: 8: 4	1,429	1,000	1,000	1,493	0,667	1,000	1,200
1: 7: 6	0,833	0,833	0,833	1,250	0,556	0,833	1,000
1: 6: 8	0,667	0,667	0,667	1,000	0,444	0,667	0,800
1: 5: 10	0,699	0,699	0,699	1,053	0,467	0,699	0,840
1: 4: 12	0,714	0,667	0,667	1,000	0,444	0,667	0,800
1: 3: 14	0,633	0,633	0,633	0,952	0,422	0,633	0,758
1: 2: 16	0,599	0,599	0,599	0,901	0,400	0,599	0,719
1: 1: 18	0,568	0,568	0,568	0,847	0,377	0,568	0,680

Продолжение таблицы 4

Continuation of table 4

k: a: b	1: 6: 8	1: 5: 10	1: 4: 12	1: 3: 14	1: 2: 16	1: 1: 18		вектор
2: 4: 2	1,500	1,430	1,400	1,580	1,670	1,760		0,087
2: 3: 4	1,500	1,430	1,500	1,580	1,670	1,760		0,092
2: 2: 6	1,500	1,430	1,500	1,580	1,670	1,760		0,095
2: 1: 8	1,000	0,950	1,000	1,050	1,110	1,180		0,061
1: 9: 2	2,250	2,140	2,250	2,370	2,500	2,650		0,138
1: 8: 4	1,500	1,430	1,500	1,580	1,670	1,760		0,095
1: 7: 6	1,250	1,190	1,250	1,320	1,390	1,470		0,077
1: 6: 8	1,000	0,950	1,000	1,050	1,110	1,180		0,062
1: 5: 10	1,053	1,000	1,050	1,105	1,170	1,235		0,065
1: 4: 12	1,000	0,952	1,000	1,050	1,110	1,180		0,062
1: 3: 14	0,952	0,905	0,952	1,000	1,055	1,118		0,058
1: 2: 16	0,901	0,855	0,901	0,948	1,000	1,060		0,055
1: 1: 18	0,847	0,810	0,847	0,894	0,943	1,000		0,052
						сумма	13,527

Table 5. Matrix of pairwise comparisons in terms of performance for different variants of the heterogeneous RSE system

k: a: b	2: 4: 2	2: 3: 4	2: 2: 6	2: 1: 8	1: 9: 2	1: 8: 4	1: 7: 6
2: 4: 2	1,000	1,000	1,000	1,330	1,670	1,670	1,330
2: 3: 4	1,000	1,000	1,000	1,330	1,670	1,670	1,330
2: 2: 6	1,000	1,000	1,000	1,330	1,670	1,670	1,330
2: 1: 8	0,752	0,752	0,752	1,000	1,250	1,250	1,000
1: 9: 2	0,599	0,599	0,599	0,800	1,000	1,000	0,800
1: 8: 4	0,599	0,599	0,599	0,800	1,000	1,000	0,800
1: 7: 6	0,752	0,752	0,752	1,000	1,250	1,250	1,000
1: 6: 8	0,752	0,752	0,752	1,000	1,250	1,250	1,000
1: 5: 10	0,752	0,752	0,752	1,000	1,250	1,250	1,000
1: 4: 12	0,752	0,752	0,752	1,000	1,250	1,250	1,000
1: 3: 14	0,752	0,752	0,752	1,000	1,250	1,250	1,000
1: 2: 16	0,752	0,752	0,752	1,000	1,250	1,250	1,000
1: 1: 18	0,752	0,752	0,752	1,000	1,250	1,250	1,000

Продолжение таблицы 5

Continuation of table 5

k: a: b	1: 6: 8	1: 5: 10	1: 4: 12	1: 3: 14	1: 2: 16	1: 1: 18		вектор
2: 4: 2	1,330	1,330	1,330	1,330	1,330	1,330		1,331
2: 3: 4	1,330	1,330	1,330	1,330	1,330	1,330		1,331
2: 2: 6	1,330	1,330	1,330	1,330	1,330	1,330		1,331
2: 1: 8	1,000	1,000	1,000	1,000	1,000	1,000		1,000
1: 9: 2	0,800	0,800	0,800	0,800	0,800	0,800		0,799
1: 8: 4	0,800	0,800	0,800	0,800	0,800	0,800		0,799
1: 7: 6	1,000	1,000	1,000	1,000	1,000	1,000		1,000
1: 6: 8	1,000	1,000	1,000	1,000	1,000	1,000		1,000
1: 5: 10	1,000	1,000	1,000	1,000	1,000	1,000		1,000
1: 4: 12	1,000	1,000	1,000	1,010	1,000	1,000		1,001
1: 3: 14	1,000	1,000	1,000	1,000	1,000	1,000		1,000
1: 2: 16	1,000	1,000	1,000	1,000	1,000	1,000		1,000
1: 1: 18	1,000	1,000	1,000	1,000	1,000	1,000		1,000
						сумма	13,171

Table 6. Matrix of pairwise comparisons in terms of resource intensity for different variants of the heterogeneous RSE system

k: a: b	2: 4: 2	2: 3: 4	2: 2: 6	2: 1: 8	1: 9: 2	1: 8: 4	1: 7: 6
2: 4: 2	1,000	1,010	1,020	1,030	0,970	0,920	0,990
2: 3: 4	0,990	1,000	1,010	1,021	0,960	0,913	1,010
2: 2: 6	0,980	0,990	1,000	1,010	0,950	0,904	0,968
2: 1: 8	0,971	0,979	0,990	1,000	0,940	0,895	0,985
1: 9: 2	1,031	1,042	1,053	1,064	1,000	0,952	1,020
1: 8: 4	1,087	1,095	1,106	1,117	1,050	1,000	1,071
1: 7: 6	1,010	0,990	1,033	1,015	0,980	0,934	1,000
1: 6: 8	1,003	0,980	1,022	1,033	0,971	0,924	0,990
1: 5: 10	0,990	1,002	1,012	1,024	0,962	0,916	0,980
1: 4: 12	0,980	0,993	1,012	1,013	0,952	0,906	0,971
1: 3: 14	0,971	0,982	0,992	1,002	0,942	0,897	0,961
1: 2: 16	0,962	0,972	0,982	0,992	0,932	0,887	0,951
1: 1: 18	0,952	0,962	0,971	0,980	0,923	0,878	0,941

Продолжение таблицы 6

Continuation of table 6

k: a: b	1: 6: 8	1: 5: 10	1: 4: 12	1: 3: 14	1: 2: 16	1: 1: 18		вектор
2: 4: 2	0,997	1,010	1,020	1,030	1,040	1,050		0,077
2: 3: 4	1,020	0,998	1,007	1,018	1,029	1,040		0,077
2: 2: 6	0,978	0,988	0,988	1,008	1,018	1,030		0,076
2: 1: 8	0,968	0,977	0,987	0,998	1,008	1,020		0,075
1: 9: 2	1,030	1,040	1,050	1,062	1,073	1,084		0,080
1: 8: 4	1,082	1,092	1,104	1,115	1,127	1,139		0,084
1: 7: 6	1,010	1,020	1,030	1,041	1,052	1,063		0,078
1: 6: 8	1,000	1,010	1,020	1,031	1,042	1,053		0,077
1: 5: 10	0,990	1,000	1,010	1,020	1,031	1,053		0,077
1: 4: 12	0,980	0,990	1,000	1,010	1,020	1,032		0,076
1: 3: 14	0,970	0,980	0,990	1,000	1,010	1,021		0,075
1: 2: 16	0,960	0,970	0,980	0,990	1,000	1,010		0,074
1: 1: 18	0,950	0,950	0,969	0,979	0,990	1,000		0,074
						сумма	13,007

Вывод: результаты расчетов показывают, что для исходных данных, представленных в табл. 2–6, рациональным вариантом разнородной системы ДЗЗ (табл. 7) является вариант № 3 – N ^КС = 2, N ^АВ = 2, N ^БПЛА = 6.

Таблица 7. Интегральная оценка вариантов разнородной системы ДЗЗ

Table 7. Integrated assessment of options for heterogeneous RSE system

№ п/п		Векторы приоритетов			Интегральная оценка варианта системы ДЗЗ M Σ
		0,181378	0,598898	0,219724
1.	2: 4: 2	0,087	1,331	0,077	0,8299
2.	2: 3: 4	0,092	1,331	0,077	0,8307
3.	2: 2: 6	0,095	1,331	0,076	0,8309
4.	2: 1: 8	0,061	1,000	0,075	0,6266
5.	1: 9: 2	0,138	0,799	0,080	0,5213
6.	1: 8: 4	0,095	0,799	0,084	0,5142
7.	1: 7: 6	0,077	1,000	0,078	0,6300
8.	1: 6: 8	0,062	1,000	0,077	0,6270
9.	1: 5: 10	0,065	1,000	0,077	0,6275
10.	1: 4: 12	0,062	1,001	0,076	0,6273
11.	1: 3: 14	0,058	1,000	0,075	0,6260
12.	1: 2: 16	0,055	1,000	0,074	0,6253
13.	1: 1: 18	0,052	1,000	0,074	0,6245
					M _Σ ^max = 0,8309

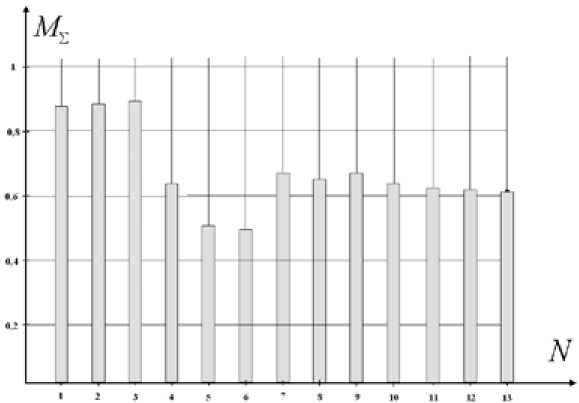
Рис. 3. Интегральные показатели эффективности системы ДЗЗ

л-а'хэ €»*,•#д V Флрамфзаачар аармнтоа r»tw.r

Прада аритегн-ае »чан«а pavwnewocr*

Вас-иджш теки к о nutпци®

Cutwofaaiwe OYHiua^J^vu? • «iiaeN^pwvti-й KUtF'K ZZk Опшмаоацда :бом а алыарма'иа-ьа aatwAwioa

Рис. 4. Концептуальная схема технологии внешнего проектирования

Fig. 4. Conceptual scheme of external design technology

Заключение

Как уже отмечалось, метод анализа иерархий целесообразно использовать на ранних стадиях жизненного цикла, т.е. при решении задач внешнего проектирования. Концептуальная схема технологии внешнего проектирования изображена на рис. 4.

На конечных стадиях жизненного цикла целесообразно либо использовать игровые по -становки [3, 4], либо применять метод сужения допустимых альтернатив [6]. Таким образом, метод анализа иерархий позволяет провести анализ проблемы. При этом проблема принятия решения представляется в виде иерархически упорядоченных:

а) главной цели (главного критерия) ранжирования возможных решений;
б) нескольких групп (уровней) однотипных факторов, так или иначе влияющих на рейтинг;
в) группы возможных решений;
г) системы связей, указывающих на взаимное влияние факторов и решений.

Метод позволяет провести сбор по проблеме; оценить противоречивость данных и минимизировать ее; провести синтез проблемы принятия решения; организовать обсуждение проблемы, способствует достижению консенсуса. Кроме того, следует отметить, что МАИ дает возможность оценить важность учета каждого решения и важность учета каждого фактора, влияющего на приоритеты решений, а также оценить устойчивость принимаемого решения.

В соответствии с формулировкой задачи принятия решения величина приоритета напрямую связана с оптимальностью решения. Поэтому решения с низкими приоритетами отвергаются как несущественные. Как отмечено выше, метод позволяет оценивать приоритеты факторов. Поэтому если при исключении некоторого фактора приоритеты решений изменяются незначительно, такой фактор можно считать несущественным для рассматриваемой задачи.

Список литературы Определение рациональной структуры разнородной системы дистанционного зондирования Земли на этапе внешнего проектирования

Reznikov B.A. System analysis and methods of system engineering. Part 1. The methodology of system research. Modeling of complex systems. MO SSSR, 1990. 522 p. (in Russia)
Ventcel' E.S. Research of operations. M.: Sov. radio, 1972. 565 p. (in Russia)
Diner I.Ya. Research of operations: textbook, ch. II. L.: VMOLA im. A.N. Krylova, 1968. 200 p. (in Russia)
Solnyshkov Yu.S. Optimization of the choice of weapons. M.: Voenizdat, 1968. 104 p. (in Russia)
Fateev V.F., Mal'cev G.N., Minakov E.P. Small space vehicles for information support. M.: Radiotekhnika, 2010. 316 p. (in Russia)
Gnusarev N.V. Geodetic and ballistic support of space systems for remote sensing of the Earth. SPb.: VKA name after A.F. Mozhajskogo, 2008. 220 p. (in Russia)
Lavrova N.P. Space photography. M., Nedra, 1983. 300 p. (in Russia)
Saati T. Decision making. Hierarchy analysis method. M.: Radio i svyaz', 1993. 278 p. (in Russia)
Moskvin B.V., Kozlov Yu.V. Mathematical model of estimation of potential possibilities of control system at detection of the opponent in the area of military operations//Kosmicheskaya kibernetika: Monografiya. SPb.: VIKU, 2003. 183-188 (in Russia)
Vaulin A.E., Volkov V.F. General methodology for solving problems of optimization of the process of maintenance of mobile objects as problems of combinatorial analysis. Deponirovannaya rukopis’ No. 228. M.: CIVTI MO SSSR, 1979. 24 p. (in Russia)
Volkov V.F., Polyakov S.A. Generating service options: sbornik algoritmov i programm tipovyh zadach, vypusk 8. L.: MO SSSR, 1987. 71-79 (in Russia)
Popovkin V.A. Indicators and criteria for balanced development of space information support. J. Strategic stability. M.: Pub. Academy of military Sciences, 2004, 4, 21-27 (in Russia)
Unmanned vehicles: methods of use in combat. J. Military thought, 2012, 3, 39-42 (in Russia)

Еще

Статья научная