Определение расчетной схемы для моделирования работы движительно-рулевого комплекса т/к типа "Астрахань"

• 1.    Введение

• 2.    Анализ расчетных схем определения ГДХ

  Рис. 1. Гидродинамические характеристики руля (изолированного)

  
  

  С учетом основных геометрических параметров пера руля (см. табл.), установленного на танкерах типа "Астрахань" (полуподвесной, полубалансирный руль с профилем NASA-0018); удлинение Л ? = 1,8; Л ? = h R2 /F R ; относительная толщина профиля t = 0,18; коэффициент компенсации К = 0,2; относительная высота балансирной части h_Rб / h_R = 0,5) по результатам многочисленных испытаний, информация о которых представлена в работах ( Соболев , 1976; Гофман , 1988), нами определены зависимости коэффициентов гидродинамической силы на руле C RX (a_R ), C_RY(a_R ) для двух основных режимов движения судна (сплошная линия – передний, пунктирная – задний ход), которые в графической форме представлены на рис. 1.

Судовой руль представляет собой крыло малого удлинения, работающее в потоке, индуцированном движением корпуса судна и работой гребного винта.

Нелинейная теория крыла малого удлинения позволяет с достаточной степенью точности рассчитать гидродинамические характеристики крыльев, близких по форме к прямоугольной, однако форма рулей в плане зачастую существенно отличаются от прямоугольной. Поэтому наиболее надежным методом определения гидродинамических характеристик судового руля C RX (a R ), C RY (a_R ) является испытание его модели в аэродинамической трубе или опытном бассейне. В данной работе использованы результаты таких испытаний. Это послужило основой для разработки расчетной схемы определения гидродинамических характеристик (ГДХ) руля т/к типа "Астрахань".

Таблица. Основные геометрические параметры руля

Высота пера руля h R , м	Площадь пера руля FR , м	Хорда руля bR , м	Максимальная толщина пера руля tR , м	Высота балансирной части h Rб , м	Площадь пера руля, попадающая в струю от винта FR ", м2
6,76	25,4	3,76	0,67	3,38	21,27

Для использования в моделировании на ЭВМ удобнее аналитическая форма представления данных зависимостей. Для получения аналитических выражений нами использованы стандартные аппроксимационные процедуры. При построении любой аппроксимации оценивалась среднеквадратичная погрешность аппроксимации и значение критерия Фишера σ ² аппр / σ ² воспр , которое сравнивалось с практическим (пороговым) значением. Всегда подбиралась такая аппроксимация, чтобы полученное отношение σ ² аппр / σ ² воспр было меньше порогового значения для заданного числа расчетных точек и выбранного вида аппроксимации, т.е. числа определенных параметров аппроксимационной функции. Результаты аппроксимации выглядят следующим образом:

при движении передним ходом:

при движении задним ходом:

C rx ( « R ) = 8,958 - 10 " ³- 6,012 - 10 ’ ⁴ « R + 4,107-10"⁴« r ², C ry ( U r ) = -3,333 - 10 " ⁴ + 36 - 10 " ³ « r + 4,214-10 " ⁴ « r ²;

(1.1)

(1.2)

C rx ( U r ) = 0,085 - 7,56 - 10^-3 « r + 8,929-10^-4 o r ², C ry ( « r ) = -6,042 - 10^-3+ 58 - 10^-3 « r - 9,012-10^-4 « r ².

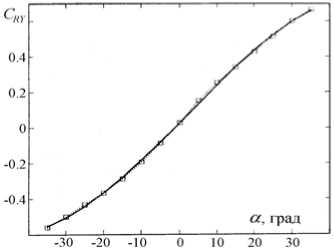
Рис. 2. Зависимость коэффициента поперечной составляющей гидродинамической силы на руле C_RY(a_R ) с учетом влияния корпуса и винта

Использовать данные зависимости для расчета поперечной и продольной составляющих гидродинамической силы на руле, установленном на судне, можно только с учетом влияния корпуса и гребного винта (рис. 2).

При движении судна по произвольной траектории влияние корпуса судна на гидродинамические характеристики руля обусловлено тремя основными факторами:

• -    наличие попутного потока за корпусом судна;

• -    наличие скоса потока из-за дрейфа кормы;

• -    наличие обшивки корпуса у верхней кромки пера руля.

Последний из названных факторов относительно мал, т.к. увеличивает поперечную составляющую гидродинамической силы на руле YR примерно на 3-5 % (Гофман, 1988), и только при малых углах перекладки руля - до 5-7°, дальнейшее увеличение угла перекладки руля делает эту добавку пренебрежимо малой. Кроме того, при минимальной загрузке танкера (судно в балласте), когда верхняя кромка пера руля может находиться в надводном положении, указанная надбавка к значению YR исключается вообще. Поэтому в дальнейших расчетах она не учитывается.

В то же время влияние свободной поверхности, зависящее от глубины расположения верхней кромки руля, аналогично влиянию твердой стенки, и этот фактор мы будем учитывать при расчете.

Как правило, швартовные операции, выполняемые танкерами с целью приема нефтепродуктов, осуществляются при минимальной загрузке, т.е. осадка, в частности, в корме da имеет минимальное значение. Например, верхняя кромка пера руля т/к "Астрахань" находится на расстоянии 7,2 м от основной плоскости, а минимальная осадка кормой около 7 м. В этих условиях неизбежно появление эффекта влияния свободной поверхности на гидродинамические характеристики руля, более того, данное влияние усиливается из-за малой скорости движения судна (Соболев, 1976). Поэтому в предлагаемой здесь расчетной схеме значение удлинения руля Ar будет округляться с учетом влияния свободной поверхности. Для этого воспользуемся аналитической зависимостью, получаемой с учетом материалов, представленных в работе Г.В. Соболева.

Значение удлинения руля с учетом влияния свободной поверхности A_rs , при Fr h < 0,5 ( Fr h -число Фруда по высоте руля h_R , Fr h = u /( gh_R )^0,5), будет определяться формулой:

A rs = A r {1 + exp(- A h / H r ) - sin[24( A h / H r )(1 - 8,3 A h / H r )]};                 (2)

при Fr h > 0,5:

A rs = A r {1 + [1,2exp{-10 A h / H r }/{1 + 2 Fr h ²}] - 0,2exp(-100 A h / H r )},          (3)

где A h - расстояние между верхней кромкой пера руля и поверхностью воды.

Корпус судна при движении образует так называемый попутный поток. Влияние попутного потока на работу руля проявляется в том, что величина вектора скорости натекания жидкости на руль меняется. Степень уменьшения скорости определяется величиной коэффициента попутного потока у_к :

U r = u (1 - У к ),                                                 (4)

здесь и - скорость судна. Коэффициент попутного потока, как правило, рассчитывается по эмпирическим формулам или графически с использованием кривых, представляющих собой зависимость коэффициента у_к от основных геометрических параметров корпуса судна. Одной из таких кривых, рекомендуемых для судов, имеющих значение коэффициента полноты C b в пределах от 0,5 до 0,8 ( Справочник , 1985), мы воспользуемся. Аппроксимационная зависимость у_к ( C b ), полученная нами с использованием графика из справочника, выглядит следующим образом:

У к = 0,4 С ь ² + 0,28 C b - 0,05.                                        (5)

Необходимо учесть, что при движении судна по криволинейной траектории или по прямолинейной траектории с углом дрейфа, что характерно для многих маневров, совершаемых во время швартовной операции, попутный поток несколько меняется. Данное изменение мы учтем, введя поправку на влияние угла дрейфа в_к в кормовой части судна. По рекомендации А.Д. Гофмана (1988), коэффициент попутного потока при движении судна с углом дрейфа примем в следующем выражении:

V k p = V . [1 — (P k /0,785) 5 ].                                                 (6)

Наличие угловой скорости l_R(tofu) меняет направление вектора скорости потока, натекающего на перо руля. Влияние вращения сводится к повороту вектора результирующей скорости на некоторый малый угол Аа, который уменьшает угол атаки руля, и его значение в общем виде может быть определено по формуле:

а = aR - Аа.(7)

Величина угла А а по своей природе равна величине угла дрейфа в районе расположения пера руля P R , который, в свою очередь, может быть определен формулой, рекомендуемой Г.В. Соболевым (1976):

Pr = $рр + $т 1r (tou),(8)

где $ р , $ _т - поправки, учитывающие спрямляющее действие попутного потока корпуса на составляющие угла натекания жидкости на перо руля, обусловленное дрейфом и кривизной траектории. Г.В. Соболев (1976) предлагает определять значения коэффициентов $ р , $ _т аналитически по формулам:

$р = <0,001/Л)Р°

$т = 2пЖ Cry“1 ,(10)

в которых λ = 2 d ² max / F db – эквивалентное удлинение корпуса судна, где d max – минимальная осадка по длине; F db – площадь диаметрального батокса; β ⁰ – угол дрейфа судна в градусах, l R – относительное отстояние оси баллера руля от плоскости мидель-шпангоута ( l R = l_RIL , L - длина судна); C_RY “ -производная коэффициента поперечной силой на руле по углу атаки а .

Рассматриваемые коэффициенты с учетом конструктивных особенностей т/к "Астрахань" по рекомендации Г.В. Соболева можно принимать равными $ р = 0,25; $ _т = 0,67 ( Соболев , 1976). Если рассчитать их значения по формулам (9-10), то они будут следующими: $ р = 0,115; $ _т = 0,289.

Уместно отметить, что методы учета влияния корпуса судна на работу руля через коэффициенты довольно разнообразны. Авторы многочисленных работ в области управляемости судна рекомендуют порой сильно различающиеся значения коэффициентов влияния корпуса, и это приводит к большому разбросу результатов расчета поперечной составляющей гидродинамической силы на руле. Поэтому, соблюдая корректность в определении гидродинамических характеристик руля, влияние корпуса через обозначенные коэффициенты будем рассчитывать по методике, предложенной в работе ( Справочник , 1985), т.к. данная методика позволяет учесть конструктивные особенности моделируемого судна.

Влияние работы гребного винта на гидродинамические характеристики руля обусловлено следующими причинами:

• –    увеличением скорости потока, набегающего на руль;

• –    уменьшением скоса потока, образующегося вследствие криволинейного движения судна.

Характер влияния работы гребного винта на гидродинамические характеристики руля зависит от того, частично или полностью перо руля попадает в поток от винта, и каким является соотношение между частями площади пера руля, попадающей в струю винта F_R " и не попадающей F_R '.

При учете влияния воздействия струи винта на работу руля, в дальнейших расчетах примем следующие допущения:

• –    cтруя движителя имеет форму кругового цилиндра с горизонтальной осью, совпадающей с осью гребного винта и диаметром, равным диаметру диска винта;

• -    скорость жидкости в струе движителя равна геометрической сумме скоростей u_R и w_a (аксиальная составляющая скорости потока от работы винта), а вне струи - скорости u R ;

• –    площадь руля F_R подразделяется на две части: расположенную в струе движителя F_R " и вне ее – F_R '. Границей между ними является поверхность цилиндра;

• –    обтекание составляющих площади пера руля ( F R ", F R ') происходит независимо, при условии сохранения характера зависимости C_RY “ для каждой части площади F R .

Существуют несколько расчетных способов определения влияния работы гребного винта на гидродинамические характеристики руля, различия между которыми определяются использованием того или иного экспериментального материала, отличающегося в основном количественным составом и местом его получения. Поэтому уместно провести сравнительный анализ расчетных способов, не только для того, чтобы выбрать один из них для использования в моделировании, но и оценить, насколько существенно могут различаться результаты расчетов по различным методикам. Такой подход, на наш взгляд, исключит возможность появления больших погрешностей при расчете одним из рассматриваемых способов.

Г.В. Соболев (1976) предложил следующую структуру выражения для определения поперечной силы на руле, работающем в струе от винта:

Yr = CryO(p/2)(ur + wa )2Fr" + (ХАрХш RFr',(11)

где p - массовая плотность воды.

Переход от значения поперечной силы на руле, работающем за пределами струи винта, к значению, определяемому по формуле (11), осуществляется через коэффициент r 1 :

r 1 = (Fr7Fr") + (Fr7Fr ")(1 + wa /и)2.(12)

Отношение вызванной работой винта осевой скорости w a к скорости в районе руля u_r определяется на основе теории идеального движителя:

(Wa /Ur ) = 0,5{1 + [2 %r/(1 + 4 Xr 2)]}-[(1 + Gt)0,5- 1].(13)

В выражении (13) использованы следующие обозначения: x_r - относительное расстояние от диска винта до центра давления руля, x_r = x_rID , D - диаметр винта; а_Т - коэффициент нагрузки винта по упору Т , определяемый формулой:

а. = 8 T/(ри2 R п D2).(14)

Г.В. Соболев (1976) считает, что расчет по формулам (12-13) дает несколько завышенное значение поперечной силы на руле. Основной причиной этого он считает завышение влияния отстояния центра давления пера руля от диска винта, ссылаясь на результаты исследований С. Окады ( Okada , 1959b). Он рекомендует учитывать влияние расстояния x_r только при выполнении условия x_r < 0,3 (при x_r > 0,3 влияние x_r на отношение w a / и , по его мнению, остается неизменным). Поскольку для т/к "Астрахань" x_r = 0,555, отношение скоростей w a / и можно определить выражением:

w a / и = 0,757 ■ [(1 + а т )⁰ ’ ⁵- 1].                                            (15)

В общем случае, используя результаты обработки большого количества экспериментов, Г.В. Соболев (1976) предлагает использовать следующую расчетную формулу.

( w a / U r ) xr . 0,3 = 0,5(1 - 0,0125 ^ ) ■ [(1 + G t )^0,5- 1].                       (16)

Известно, что вызванная скорость в струе гребного винта складывается из двух составляющих: аксиальной w_a и тангенциальной w_t . Влияние последней на угол атаки а заметно в том случае, если граница струи сдвинута за пределы контура пера руля. Указанный фактор приводит к возникновению дополнительной нагрузки на руле, для компенсации которой требуется перекладка руля на так называемый угол нулевой поперечной силы а 0 , значение которого может быть определено по формуле, предложенной Окадой ( Okada , 1959a):

О = 0,01 + 0,04(1 - X p D / H) ,                             (17)

где Х р - относительная поступь винта, Х р = и р /nD (и р = u_r ), n - обороты гребного винта; Н - шаг винта. Очевидно, что в этом случае угол атаки будет равен:

а = O r - e R - O q .                                         (18)

Надо отметить, что в случае с т/к "Астрахань" нижняя кромка пера руля совпадает с границей струи винта и, следовательно, в дальнейшем будем принимать а 0 = 0.

Учесть влияние попутного потока Г.В. Соболев предлагает введением дополнительной поправки к производной подъёмной силы на руле:

r2 = (1 - V)2.(19)

Таким образом, коэффициент поперечной составляющей гидродинамической силы на руле определится выражением:

Cry = r 1 r2Cry^Or - eR),(20)

где производная поперечной составляющей по углу атаки а, C RX ^a определяется по интерполяционной формуле Прандтля:

CryO = 2п^/(2 + Ar ),(21)

а конечное выражение для расчета поперечной составляющей гидродинамической силы на руле с учетом (12-13) или (16-19, 21):

Yr = Cry (ри2/2)Fr.(22)

В основу расчетного метода, разработанного А.Д. Гофманом (1988), положены данные экспериментального исследования поперечной силы руля, принятого в качестве стандартного, имеющего удлинение X R = 1,0 и полностью попадающего в струю винта. Размах и хорда стандартного руля равны диаметру D , коэффициент компенсации K = 0,33, отстояние передней кромки пера руля от винта 0,5 D .

Профиль стандартного руля NACA-0012. Диапазоны варьирования параметров, определяющих режим работы руля: -35° <  a_R < 35°; 0 <  с_т < 50°; 0 <  e R - 60°. Результаты испытаний представлены в виде зависимости безразмерной поперечной силы руля c Y от основных параметров, характеризующих поток, обтекающий перо руля a R , c T , e R :

C Yst = 2 Y r pU R F p ,                                      (23)

в данном случае F_p - площадь сечения диска винта.

Во всем принятом к рассмотрению диапазоне углов перекладки руля, углов дрейфа и коэффициента нагрузки винта по упору для определения величины c Yst можно принимать линейную зависимость вида c Ys = c_Yst^aa_R ( Гофман , 1988), причем производная c_Yst^a = dc_YstIda линейно зависит от коэффициента нагрузки. В наших расчетах мы будем использовать полученную нами аппроксимационную формулу:

C Yst ^a = 1,25 c t + 3,0.

Общее выражение для безразмерной поперечной силы руля произвольной в плане формы, пересекающего всю струю движителя и имеющего выступающую из струи часть, имеет вид:

C y = а^ я - А рk Y [(2 k , + A r " - 1)<4 A r " k , - 3 A r " - 4 k , + 6)]I[ A r "( A r " + 1,0)( A r " + 2)] + + (8 A R F r )*( a R - P r )/(1 + A r ') D ²,                               (24)

где А в - угол отклонения струи движителя в косом потоке, А в = k p e R , где значение k p определяется графически по материалам ( Гофман , 1988). Используя те же материалы, мы получили следующие аналитические зависимости:

1,                                                       если c_T < 1;

k p =  [ с т I( c t ² + C t + 2)] + (0,11| c t - 2 | / с т ) + 0,001( с т ³ - 4),   если 1 <  c_T < 4;              (25)

[cT/(cT2 + cT + 2)] + (0,11|cT- 2|/cT) + 0,12,            если cT> 4, kY - коэффициент, учитывающий уменьшение поперечной силы руля при отклонении струи движителя косым потоком. Из (Гофман, 1988) известно, что kY зависит от расстояния между диском винта и точкой, где измерено отклонение струи xp. В нашем случае с учетом конструктивных особенностей движительно-рулевого комплекса т/к "Астрахань", xp = 0,7 ( xp = хрID), в пределах возможных углов перекладки руля -35° < aR < 35° kY = 1 (Гофман, 1988).

k _A - коэффициент, учитывающий отличие значений удлинений A R ', A R " ( A R = A R ' + A R ", A R ' - удлинение части пера руля, не попадающей в струю от винта; AR" - удлинение части пера руля, попадающей в струю от винта) рассматриваемого руля и стандартного руля ( X_Rst = 1,0), его значение зависит от коэффициента нагрузки винта по упору с_Т и может быть определено из графика, представленного в работе ( Гофман , 1988). Для использования в дальнейших расчётах на ЭВМ графическая форма преобразована нами в аналитическую и выглядит следующим образом:

1,5 - 0,052[1 + 0,121(4 - ст)(1’977 - °';с)] ■ ст, если 0 < ст < 4;

если 4 <  с_т <  10;

если 10 <  с_т <  20; если с_т > 20.

k = 1,292 - 0,01(6 + с т ) ■ 1д( с т - 3),

^A     1,292 - 0,21[(0,0024 с т ² + 0,1809 с т + 1)1(1 + 0,3 с т )] ■ 1g( c - 3),

1 + 1,726 - ст"\

При выполнении швартовных операций достаточно часто гребной винт работает в швартовном режиме. В этом случае, в силу неопределённости, возникающей при расчёте коэффициента нагрузки по упору ( с_т ^ « при и ^ 0), для определения значения поперечной силы на руле при работе гребного винта в швартовном режиме Y R _шв используем зависимость, предложенную А.Д. Гофманом (1988):

Y r шв = k R шв Рп ² D ²

где n - обороты движителя; k_{R шв} - безразмерный коэффициент, зависящий от коэффициента упора винта К Т , работающего в швартовном режиме ( и = 0 ):

0,011 a_R ° К Т „Д" _R ;   если a_R < 25°;

0,175 К Т _шв / Х " _R ;       если 25°< a_R < 35°.

В условиях выполнения швартовной операции судно достаточно часто может двигаться по инерции, при застопоренном или свободно вращающемся гребном винте. В этом случае эффективность работы руля уменьшается не только по причине отсутствия гидродинамической струи от движителя, но и из-за определенного влияния неработающего винта на характер потока, набегающего на перо руля. В этом случае ряд исследователей (Гофман, 1988; Соболев, 1976) рекомендует уменьшать значение коэффициента поперечной силы на руле, примерно на 30 %. Гофман для ориентировочной оценки указанного влияния предлагает следующую расчетную формулу:

Cry = 0,7 [2п/(1 + 2 AR)] ■ (aR - Pr).(29)

Для перехода от значения коэффициента поперечной силы о_у к C RY необходимо использовать зависимость:

CRY = (FP/FR) ■ Оу.

Оценку величины продольной составляющей силы на руле можно выполнить, воспользовавшись формулой К.К. Федяевского ( Соболев , 1976):

Crx = Crxo + к'(sna/Г + 2(sina)3,(31)

где C_RX0 - коэффициент продольной составляющей силы на руле при нулевом угле атаки, вычисляемый по формуле:

Crxo = (0,0221 - 0,0023logRe)CX,(32)

к А - коэффициент, определяющий зависимость продольной силы на руле от удлинения руля X_r , для его определения нами получена следующая расчетная формула:

кА = 0,65 (Ar)0,5 - 0,042r;(33)

R e - число Рейнольдса, R e = uL / v ; v - кинетическая вязкость воды, С х - коэффициент, учитывающий телесность пера руля:

Сх = 4,96 7 + 0,76.(34)

Р.Я. Першиц предлагает следующую расчетную схему определений поперечной составляющей гидродинамической силы на руле:

Yr = Cry(P2W FRn;(35)

Cry = Cry“ [ aR - $ЦЗ + 1R ®/u)].(3 6)

Значение C_RY^a определяется выражением:

CRYa = - (2nCr)/(1 + 2/A),(37)

где

Cr = - 0,266Xr + 1,133.(38)

Данная формула получена из графика зависимости C_r = f( X_r ), представленного в работе Р.Я. Першица ( Справочник , 1985). Приведенный коэффициент влияния корпуса и винта представлен в виде произведения:

« = ге^Жр,(39)

ж_к0 , ж_р - коэффициенты влияния корпуса и винта, соответственно. При малых углах дрейфа (в < 15 ° ):

«р = (Fr ' + Fr ''(1 + От)0,5)/(Fr ' + Fr "(1 + От)),(40)

а значение ж_к0 принимается в зависимости от размещения пера руля относительно корпуса судна, в частности, на т/к "Астрахань" зазор между дейдвудом и передней кромкой руля равен 3,0 м, а его отношение к хорде равно ~ 0,7, т.е. больше 0,5, следовательно «_{к 0} = 0,3. При больших углах дрейфа

Р.Я. Першиц рекомендует использовать несколько иную зависимость для определения значения коэффициента ж, в этом случае

« к = 0,5[1 + ж_ю - (1 - « ko )cos2Р м ] .

arccos (ucosp/u_M ),     если - u sln ^ + l_R® < 0;

- arccos (ucosp/u_M ), если - uslnp + l_R® > 0.

Здесь в м - местный угол дрейфа.

Р м =

В выражении (42)

u_M = [( u cos ^ )² + ( l_R® - u sln ^ )²]^0,5.

Применительно к расчёту управляемости на больших углах дрейфа:

Yr = Cry (0,5pu2Fr + cT),(44)

где значение c определяется формулой:

F r "/ F p ,   если F r "/ F p < 1;

c 1,         если Fr"/Fp > 1, а коэффициент поперечной силы будет равен CRYa а. При а > акр Р.Я. Першиц предлагает принять условие CrY ~ 1,0. В режимах, близких к швартовному, рекомендуется считать, что

Cry = CRYa slna.(46)

И при этом расчёт производной C_RY^a выполняется по формуле:

CRY = Cry“шв + (CRYaиз - CrY^M (2 - $р),(47)

в которой C_RY^a_шв - производная коэффициента C RY на швартовном режиме. Она может быть рассчитана с учётом зависимости (27) или принята равной 0,82 ( Справочник , 1985).

Производная коэффициента C RY для изолированного руля C_ry “ _u3 определяется с использованием зависимостей, представленных на рис. 1, при этом а = a_R - «в м ; се = «« р _шв , а значение коэффициента влияния винта рассчитывается по формуле:

æ р шв = æ р + 0,65 x ' R æ p (1 – æ p ),                                 (48)

в ней x 'R = (x 'R + bR)/D,                                            (49)

где x ' R – расстояние от диска винта до передней кромки пера руля.

Дополнительное сопротивление от перекладки руля Р.Я. Першиц рекомендует определять только с учетом зависимости C_RX(а), в этом случае продольная составляющая гидродинамической силы на руле определяется выражением:

X r = C rx ( a)(0,5pU F r + cT).                             (50)

Расчет поперечной и продольной составляющей гидродинамической силы на руле при движении судна задним ходом ведется по представленным выше зависимостям, полученным для движения передним ходом, но при этом влияние работающего движителя и корпуса не учитывается. На переходном режиме движения (судно движется вперед, винт работает на задний ход или наоборот) расчет ведется с учетом фактического влияния движителя и корпуса на работу руля.

Итак, мы рассмотрели три расчетных схемы, каждая из которых имеет характерные особенности в методике определения влияния корпуса судна и гребного винта на значение поперечной составляющей гидродинамической силы на руле. Существуют также несколько иных способов расчета указанного параметра, которые принципиально не отличаются от рассмотренных, поэтому здесь мы их не приводим.

На рис. 3 представлены результаты расчета поперечной составляющей гидродинамической силы на руле в соответствии с расчетными схемами, предложенными авторами работ ( Соболев , 1976; Справочник , 1985; Гофман , 1988) для случая движения на прямолинейном курсе без дрейфа (а) и при движении на криволинейной траектории (б).

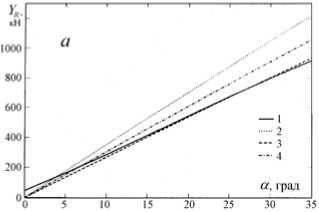
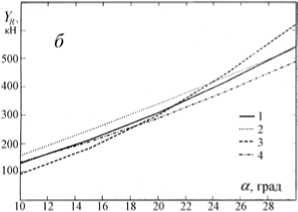
Рис. 3. Зависимость поперечной составляющей гидродинамической силы на руле от угла перекладки руля

Y R (a_R ), рассчитанная:

1 – с учетом ГДХ изолированного руля; 2 – по Гофману; 3 – по Першицу; 4 – по Соболеву

3. Выводы

Большой разброс значений поперечной составляющей гидродинамической силы на руле, полученных по результатам расчета, не позволяет с достаточной уверенностью использовать рассмотренные расчетные схемы для адекватного математического моделирования работы движительно-рулевого комплекса танкера. В этом случае результаты расчетов, полученные с использованием зависимостей (1-2) и с учетом конструктивных особенностей корпуса танкера и взаимного расположения гребного винта и руля, можно считать наиболее приближенными к реальным значениям рассчитываемого параметра. Поэтому при выполнении моделирования, с целью разработки оптимальных способов маневрирования судна, мы предлагаем использовать именно эту расчетную схему.