Определение расчетных зависимостей рабочих параметров суперкавитационного испарителя

В последние три-четыре десятилетия мировым сообществом достигнуты серьезные успехи в области разработки техники и технологии опреснения морских вод с целью удешевления производства пресной воды. Эти наработки с успехом применяются и в теплоэнергетике. Значительный прогресс достигнут при разработке установок термодистилляционного получения пресной воды высокого качества. Этот метод становится предпочтительным для применения в теплоэнергетике вместо установок ионообменных технологий, использование которых связано со значительными трудностями, встречающимися при решении задач ликвидации отработанных регенерационных растворов ионообменных установок.

Сравнительный анализ различных схем опреснения и способов улучшения теплообмена в испарительных установках показывает, что наибольшей эффективностью отличаются методы, в которых изменение гидродинамических характеристик течения жидкости приводит к увеличению энергонапряженности теплообменной поверхности. В этом направлении перспективно использование режимов развитой кавитации, поскольку особенности конструктивного оформления суперкавитационных аппаратов и возможность за счет гидродинамики поддерживать устойчивую границу раздела между жидкой и паровой фазами обусловливают некоторые преимущества этого способа испарения по сравнению с известными методами.

В отличие от известных методов процесс испарения в аппаратах суперкавитирующего типа осуществляется за счет создания развитого кавитационного течения при обтекании не

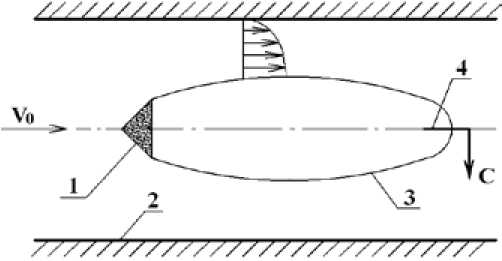
Рис. 1. Принципиальная схема суперкавитационного испарения: 1 – кавитатор; 2 – труба круглого сечения; 3 – суперкаверна; 4 – отбор пара из каверны догретой жидкостью кавитатора с последующим отбором пара из образовавшихся каверн [1]. Анализ исследований развитых кавитационных течений показал, что в большинстве работ по определению форм и размеров каверн, как теоретических, так и экспериментальных, в качестве кавитаторов в основном использовали диски, конусы и шары [1]. В настоящей работе исследовались режимы кавитационного испарения при обтекании конусов с различными углами раствора и диаметром основания. На рисунке 1 представлена схема суперкавитационного испарения.

Одновременное существование граничной динамики, фазового перехода и сильного изменения плотности значительно затрудняет задачу исследования рабочих процессов термокавитационных испарителей. Проведенный обзор современных методов математического моделирования кавитационных течений [2] позволил определить адекватный подход к решению данной задачи.

Математическая модель суперкавитационного испарителя

Здесь для оценки поверхности кавитационного испарения используется модель двухфазного гомогенного потока, в которой поток рассматривается как гомогенная смесь. Эта модель основана на предположении локального кинематического и термодинамического равновесия между фазами и не предполагает поверхность раздела между паром и водой. Объемная доля фазы может изменяться от нуля до единицы в зависимости от занимаемого пространства в двухфазном потоке. Задача рассматривается в стационарной двумерной осесимметричной постановке и предполагает решение уравнений (1)-(6).

Уравнение неразрывности для каждой фазы α

• ^V" ( Wa u m ) = ^ lv ,                                                          (1)

где r_a - объемная доля фазы а ; р_а - плотность фазы а , кг/м³; S lv - массовая скорость образования фазы, кг/м³с; u m - скорость смеси, м/с.

Уравнение движения для смеси

• V" ( P m U m U m — Ц m ( v U m + ( V U m ) T )) = —V P ,                                 (2)

где р m - плотность смеси, кг/м³; ц m - коэффициент кинематической вязкости смеси, Па^с; P -давление, Па.

Турбулентность учитывается использованием к - е модели. Уравнения переноса для кинетической энергии турбулентности к , м²/с², и ее диссипации е , м²/с³:

V-(P mkUm ) = V-

(и. + )v к к    °к) )

+ ^G — Р m ^ ,

V-(p m £ Um ) = V.

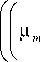
+ k

°£) )

ε            ε2

⁺ C i ~G ^- C 2 p m —, kk

где G - скорость генерации турбулентности, ц t - турбулентная вязкость. Эмпирические константы имеют следующие значения: о _к = 1; о_е = 1,3; C 1 = 1,44; C ₂ = 1,92. Так как фазы должны полностью заполнять весь объем, то принимается следующее условие:

N

У Г а = 1- α

α

Для массовой скорости образования фазы используется кавитационная модель [3]:

F vap

Slv = ^

3rnuc (1 - rv )Р v / 2 Pv - PI

R B        3 ρ l

F   3 r v Р v

^Fcon   _{RB    3   ρ l}

при P < Pv при P > Pv,

где r_пис – объемная доля зародышей («ядер») кавитаций; R_B – радиус зародыша кавитации, м. При моделировании применялись следующие параметры модели: R B = 10 ⁶ м, г пис = 5^10 ⁴, F var = 50 и F„ = ⁰⁰¹

Для замыкания системы уравнений принимали следующие граничные условия: на входе в рабочий участок задавалась скорость, линейный масштаб и интенсивность турбулентности, объемные доли пара и воды, а на выходе – давление.

Результаты численного исследования

На первом этапе исследований были проведены расчеты для холодной воды, температура которой составляла 20 ° С, такой режим можно считать предельным по температуре ведения процесса для кавитационного испарения. На втором этапе расчеты проводили для горячей воды. Температура воды принималась в диапазоне 110-120 ° С. Температурный интервал был принят в соответствии с максимальной температурой воды на входе в первую ступень испарения большинства современных испарительных установок [4].

На рисунке 2 в качестве примера представлена доля пара в смеси при различных числах кавитации. Численный эксперимент проводили при постоянном значении числа Фруда (37,4) и степени стеснения потока (0,29).

На рисунке 3 отображена зависимость относительной длины каверны от числа кавитации, указывающая на хорошее согласование расчетных и экспериментальных значений. Рассогласование расчетных и экспериментальных данных может считаться допустимым из-за условности – 46 –

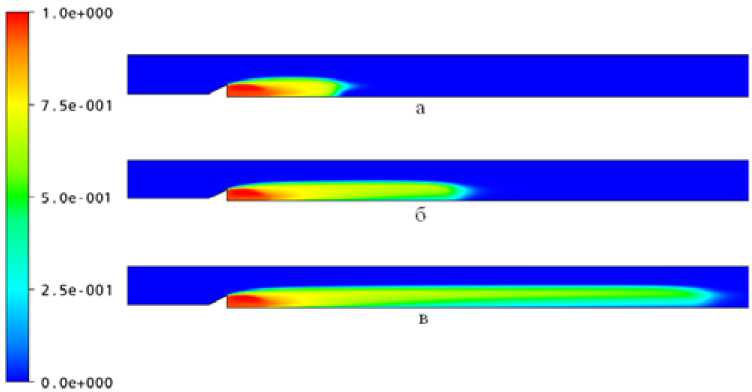
Рис. 2. Расчетные результаты распределения доли пара при разных числах кавитации: а – число кавитации 0,47; б – число кавитации 0,465; в – число кавитации 0,46

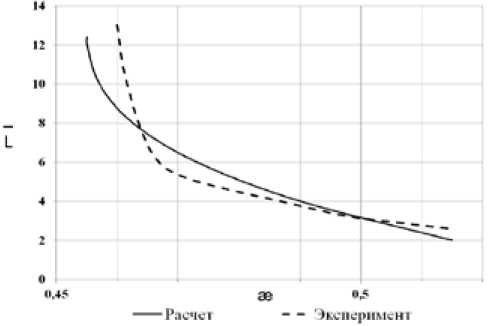
Рис. 3. Зависимость относительной длины каверны от числа кавитации, степень стеснения потока – 0,29; число Фруда – 37,4

самого понятия длины каверны. Анализ полученных результатов показывает, что при постоянных значениях коэффициента стеснения потока и числа Фруда уменьшение числа кавитации приводит к росту размеров каверны. При постоянных значениях коэффициента стеснения потока и уменьшении числа Фруда наблюдается уменьшение размеров каверны (рис. 4).

Увеличение степени стеснения потока и уменьшение чисел Фруда приводит к увеличению чисел кавитации, при которых реализуется предельная форма суперкавитационного обтекания, когда площадь миделевого сечения каверны и ее длина при данном стеснении достигают максимальной величины.

Зависимости относительной длины каверны от числа кавитации и температуры воды на входе в рабочий участок при постоянных значениях коэффициента стеснения потока и числа

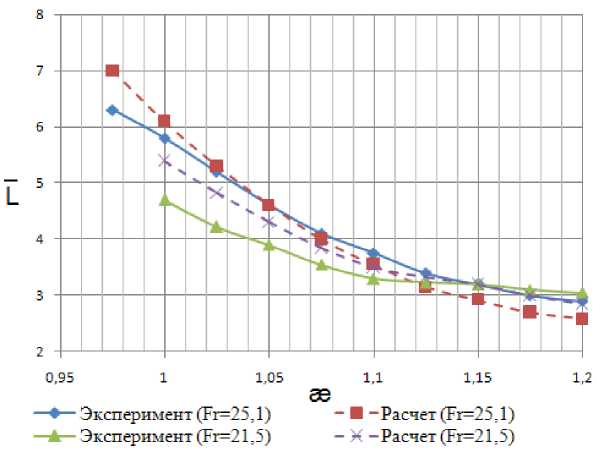
Рис. 4. Зависимость относительной длины каверны от числа кавитации, степень стеснения потока – 0,45

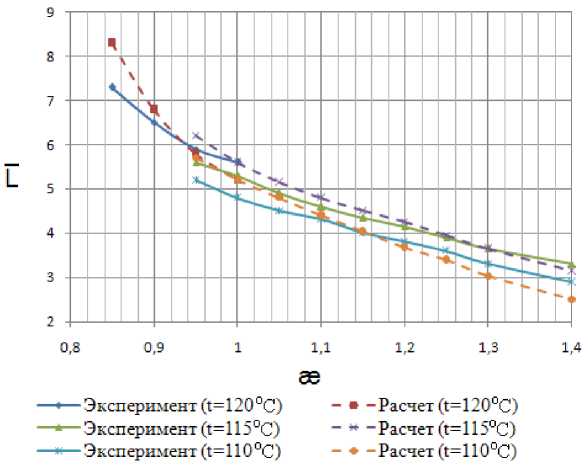
Рис. 5. Зависимость относительной длины каверны от числа кавитации, степень стеснения потока – 0,24; число Фруда – 13,6

Фруда показаны на рис. 5. Видно, что при постоянном значении коэффициента стеснения потока и числе Фруда увеличение температуры воды на входе в рабочий участок приводит к росту размеров каверны. С увеличением температуры связан рост давления насыщения в области кавитации и, следовательно, реализуются режимы кавитационного обтекания с малыми числами кавитации.

Выводы

Полученные расчетные завмсимости хорошо согласуются с экспериментальными данными, что дает возможность дальнейшего использования представленной математической модели для анализа и совершенствования рабочих процессов в суперкавитационных испарителях. В статье найдены зависимости безразмерных критериев, характеризующих рабочие процессы, протекающие в суперкавитационных испарителях, которые могут быть использованы для определения их режимных и конструктивных параметров. Суперкавитационный метод является перспективным способом опреснения и требует дальнейшего изучения и развития.