Определение разрядности коэффициентов цифровых фильтров

Известно, что ошибки квантования коэффициентов передаточной функции цифровых фильтров или коэффициентов импульсной характеристики КИХ-фильтров, обусловленные операцией округления или усечения длительности кодового слова, не относятся к шумам квантования и учитываются в искажении частотных характеристик фильтра [1]. При анализе искажений частотных характеристик предполагается, что ошибка округления при квантовании коэффициентов фильтра является случайной величиной с равномерным законом распределения вероятностей, что позволяет оценить не только среднеквадратическое отклонение амплитудно-частотной характеристики (АЧХ) реализованного фильтра от АЧХ идеализированного фильтра, но и определить число разрядов кодовых слов коэффициентов исходя из заданной погрешности на АЧХ фильтра [2].

При этом влияние квантования коэффициентов учитывается введением паразитного фильтра, включенного параллельно идеализированному фильтру, а определение разрядности производится методом перебора, последовательно увеличивая число разрядов [3]. Имеются и другие методы определения разрядности коэффициентов, например, метод, основанный на использовании функции чувствительности амплитудно-частотной характеристики фильтра (или положения полюсов или нулей на z-плоскости) к изменению коэффициентов [4]. В настоящей статье исследуются не рассмотренные в вышеупомянутых работах методы определения разрядности коэффициентов рекурсивных фильтров при заданной погрешности на искажения АЧХ фильтра.

Определение разрядности коэффициентов на основе передаточных функций

Представим передаточную функцию цифрового фильтра с точными коэффициентами в виде

м

/=1

При квантовании вместо точных значений коэффициентов dm И 6/ получаем приближенные их значения а_т и bi , при этом ошибки квантования коэффициентов могут быть представлены следующим образом

— ^ т   ^^{т ;}

^еы =b_t -bi ^. (3)

Пусть х^пТ^ и у^пТ^ – входная и выходная последовательности идеального фильтра, а у^пТ ) – отклик реального фильтра на входную последовательность х^Т⁷). Используя разностное уравнение, найдем ошибку выходной последовательности из-за квантования коэффициентов [1]:

е(пТ) = у(пТ)-у(пТ) =

м

Е _апДпТ-тГ)

т=0

^ЫУ^пТ-Щ

м

М _           N _ _

Z а„А^пТ-тТ^Т.Ь1У<п^т-Ю

_ т=0                   1=\

МN

= Е еа(т)х{пТ-тТ^ + ^еь^^Ъty{nT-Щ + т=0/-1

NN

+ Zbie(nT-lT)-Ze_b(l)e(_nT-lT) .

/=1/=1

Пренебрегая последним слагаемым как величиной второго порядка малости, заменим дискретные свертки в выражении (4) произведением z-изображений соответствующих функций:

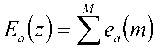
z'”;

w=0

Eb^V^b^²"¹ S /=1

e^-^htV';

и=0

Вт^^^-^^г"1;

/=1

имеем

E(z)s₀₀(z) = £_o(z)^(z) + E₆(z)y(z) . (9)

Поделим правую и левую части урав-нения (9) на НДг^ВДг) = A_m(z), тогда, учитывая (1), получим

E^

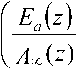
IM, B^

X^ . (10)

Если входным сигналом (входной последовательностью) является дискретная импульсная функция

3^ = 1 , тогда уравнение (10) можно записать в виде

E^

= №^

и рассматривать его как относительную погрешность передаточной функции, обусловленную квантованием коэффициентов передаточной функции.

Из выражения (12) следует, что максимальные значения погрешностей достигаются в нулях и полюсах передаточной функции H(z) фильтра.

Заменяя переменную на , получим выражение для относительной погрешности частотной характеристики фильтра в виде

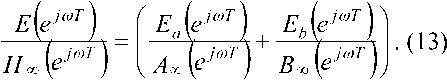
Полагая, что ошибки eM и вь (^/) коэффициентов am и bi передаточной функции фильтра из-за операции округления независимы друг от друга являются случайными величинами с нулевыми средними и одинаковыми максимальными значениями, равными половине шага квантования A:

кН=|=2Ч“’- кЛ^^г^’ли)

где b – разрядность двоичного кода, представим относительную погрешность АЧХ как среднеквадратичную сумму ошибок квантования следующим образом

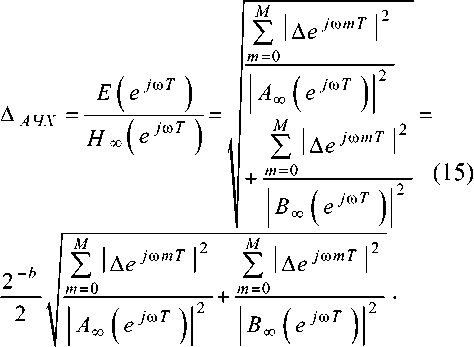
Решив уравнение (15) относительно величины b , определим разрядность коэффициентов фильтра при заданной относительной погрешности ^АЧХ амплитудно-частотной характеристики фильтра по вероятностной модели ошибок квантования коэффициентов

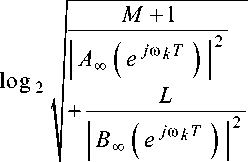
_v - log 2 ( А А ЧХ )

где ^Юк – соответствующие частоты нулей и полюсов частотной характеристики H^^jmT\ При этом разрядность выбирается наибольшей из полученных значений разрядностей на частотах co_K .

Для детерминированной модели ошибок квантования разрядность коэффициентов определяется по формуле

1 . (17)

При этом заметим, что коэффициенты, точные значения которых кратны 2 , сохраняют свои значения, и их не надо учитывать при определении погрешности частотной характеристики фильтра и соответственно при расчете разрядности.

Если требование на АЧХ фильтра задано на дисперсию частотной характеристики фильтра, тогда представив дисперсию в виде

С учетом (21)-(22) определяем разрядность коэффициентов по формуле

6 = int

log 2

D_H ^h =^- j \н\е^^т )-Я_ж (e^^r )|² 6/0=

7W + 1 _r    1 dz

2tV В (-) -

4 ₊ jv_ г Лоо(2)Лоо(2"¹) dz

4 ^ic B\^ z

-log 2

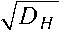
-1,79;

T

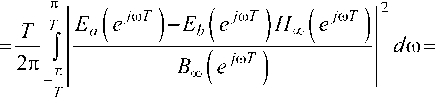
здесь

В ^^B^B^z ^!);

51(2) =|

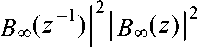
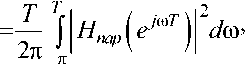
где черта сверху означает усреднение по времени. Полагая, что входная последовательность ошибки              статистически независи мые величины и что

Определение разрядности коэффициентов на основе функций чувствительности

Чувствительностью некоторой функции     к изменению параметра называется предел отношения относительного изменения функции к относительному изменению параметра

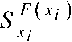
lim

Ax ^ ^ 0

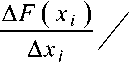
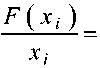
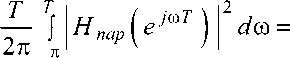
SF(xj ) 8x,

F(xi)

2л у

\Hnap(2)H_nap(z ’)z ^xdz c

из формулы (18) с учетом (10) и (19) имеем [1]:

ojv —E‘

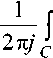
Е^-Еь^-Н^

EcP2izMi2n!_di2i

Sool-"1)

В качестве функции может быть выбрана комплексная частотная характеристика цифрового фильтра или такая величина, как полюс передаточной функции. В качестве параметра могут быть взяты коэффициенты фильтра или координаты полюсов и нулей на комплексной плос кости z. Функции чувствительности передаточной функции      фильтра к изменению коэффициентов        имеют вид

T^W

F1=O

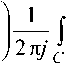
№) /7=1

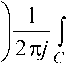
1 dz ---------------zi---^

B^B^z ) 2

Ejpdjz"¹) dz

Isoo^"1)!2^»^)!2 z

5Ht-d _ ^77c	AZ)am _ anF ’” .	(25)
a" нж	А)дат ^(z) ’
_ dHQ b‘ " hj	АД ь,^ A^db, dm(z)	(26)

где символ Е означает усреднение по времени. При квантовании коэффициентов ошибки округления удовлетворяют соотношениям

Полагая, как и раньше, что ошибки округления при квантовании коэффициентов

М-Фу; Mo|s|; (2D

Ы(”0 = (М + 1)Я y,e¹_b(.nT') = N^-. (22)

m=0                ^  /7=1             12

к,М4 = 2~1‘Х Ml = I = 2~(S+1)

одинаковы для всех коэффициентов, запишем относительные погрешности квантованных коэффициентов в виде

= A x ₌ A 2a, ’ ^Ы 2b, ‘

Поскольку требования заданы на АЧХ фильтра, то при определении разрядности перейдем в частотную область, разделим функции чувствительности в частотной области на значения соответствующих коэффициентов, просуммируем полученные выражения и получим нормированную суммарную чувствительность

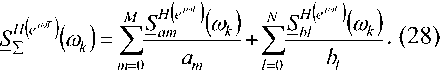
Определив максимальное значение суммарной чувствительности, запишем относительную погрешность АЧХ фильтра

A _ Mjtok, ^АЧХ- „/ .  \

HU®k)

= S_t:\^2^. (29)

Из уравнения (29) находим разрядность коэффициентов по детерминированной модели ошибок b = int log2

—Zmax ^(^(t )| ^gzA™) 1- (30)

Разрядность коэффициентов по вероятностной модели ошибок можно найти, если в формулу (29) подставить среднеквадратичное значение суммарной нормированной чувствительности

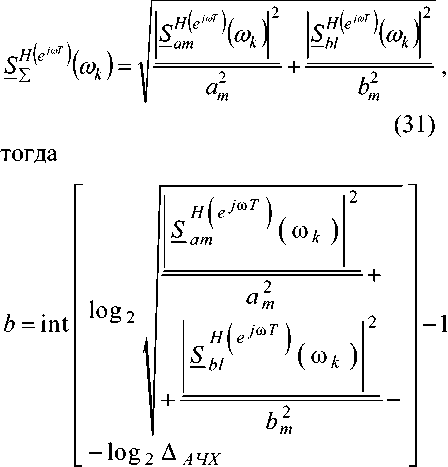
Можно показать существование глубокой связи между определением разрядности коэффициентов по формулам (16)-(17) и по формулам

(31)-(32). Если функции чувствительности – см. формулы (25)-(26), умножить на относительные величины ошибки квантования соответствующих коэффициентов – см. формулу (27), и сложить полученные результаты, то получим выражение относительной погрешности передаточной функции (10) вида

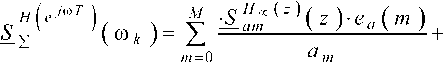
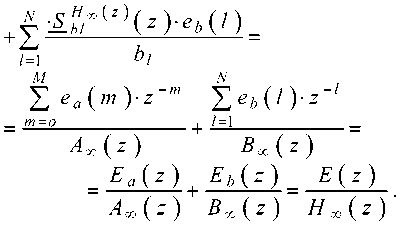
Выводы

В работе рассмотрены методы определения разрядности коэффициентов функции цифрового фильтра по заданному допустимому значению ошибки амплитудно-частотной характеристики цифрового фильтра на основе ошибки передаточной функции и на основе функции чувствительности передаточной функции к коэффициентам. Показано, что значения разрядностей коэффициентов, определяемые рассмотренными методами, совпадают, но при этом метод на основе функции чувствительности более прост. Практика применения методов показала, что для передаточной функции звена второго порядка разрядность коэффициентов, определяемая по вероятностным моделям ошибок квантования, по крайней мере, на единицу меньше разрядности коэффициентов, определяемой по детерминированным моделям ошибок квантования.