Определение резонансных диаграмм лопастей малогабаритных ветроэнергетических установок

Введение. Источники возобновляемой энергии – один из современных способов получения электроэнергии с использованием природных явлений. Ветроэнергетические установки среди прочих нетрадиционных источников получили самое широкое распространение. Ветроэнергетика вызывает повышенный интерес по целому ряду причин. Главной из них является независимость ветро-генератора от общей системы электроснабжения, отсутствие выбросов. При правильном выборе ветрогенератора его использование приносит существенную экономию средств. Это особенно актуально при долгосрочной эксплуатации.

Наилучшие характеристики показывают ветроэнергоустановки (ВЭУ), обладающие системами автоматического управления. В случае использования системы автоматического управления с нагрузкой необходимо добиваться изменения частоты вращения при частотах, близких к резонансным. Только в этой ситуации можно добиться длительной работы ВЭУ. Наиболее опасны резонансные колебания лопастей в направлении перпендикулярном плоскости вращения. Частоты таких колебаний могут быть определены аналитически.

Методика построения резонансных диаграмм. Ветротурбина, создавая крутящий момент на валу генератора, создает и переменные нагрузки, обусловленные как наличием косой обдувки, так и дисбалансом самого ветроколеса. Амплитуда переменных нагрузок зависит от конструктивных особенностей лопасти и режимов работы ветроэнергетической установки. Кроме того, амплитуда колебаний лопастей зависит от того, насколько близки частоты внешних сил, возбуждающих колебания к собственным частотам лопастей. При совпадении частот происходит резкое увеличение амплитуды, обусловленное резонансом. Для определения резонансов ветротурбины необходимо построить резонансную диаграмму колебаний в плоскости поперечной плоскости вращения.

В настоящее время существует ряд методов расчета резонансных характеристик лопастей. Однако для малых ВЭУ, самой нижней ценовой категории, необходим наиболее простой метод, расчет которого представлен ниже.

В общем случае уравнение свободных колебаний лопасти в этой плоскости имеет вид [2] ( ЕД - У W- ( ^У Л ) ' + m _л у л = 0,                           (1)

где E_л – модуль упругости материала лонжерона лопасти; I_лх – момент инерции сечения лонжерона лопасти относительно горизонтальной оси; y_л – перемещение лопасти в вертикальном направлении; N₄₆ - центробежная сила; m _л - погонная масса лопасти.

Штрихами обозначено дифференцирование по радиусу, а точками – дифференцирование по времени.

При использовании жесткой заделки лопастей можно принять следующие граничные условия у , m =0, у', m =0, (EI у”) „ =0, (EI „ =0.

^ул ( r = 0)       , ^ул ( r = 0)       , V л ЛХ^уЛ7Г = R , V л ЛХ^уЛ7Г = R

Решение уравнения (1) можно представить в виде произведения двух функций

Ул (r, t) = ^( r)-8( t),(2)

где ^ ( r ) - функция только радиуса; 8 ( t ) - функция только времени.

Соответственно выражение распадается на уравнения

8( t) + Рлх 28( t) = 0,(3)

где р_лх – угловая частота собственных изгибных колебаний лопасти.

[EI^(r)]" - [N^'(r)]' - Рлх2тлКr) = 0.(4)

Для решения этих уравнений наиболее распространенным является способ Б.Г. Галеркина [3], согласно которому решение ищется в виде ряда

n

Кr) = Е С,ф,(r),(5)

I = 0

где С , - постоянные коэффициенты; ф , .( r ) - заранее заданные функции радиуса, удовлетворяющие граничным условиям; n – количество членов ряда, принимаемых к расчету.

Функции ф , ( r ) выбираются так, чтобы каждая из них удовлетворяла всем граничным условиям, а вся совокупность функций ф , ( r ) сходилась к какому-то значению, а не расходилась. Можно воспользоваться функциями Крылова при соответствующем выборе коэффициентов.

Согласно методу Галеркина ряд (5) подставляется в равенство (4), каждый член умножается на одну из функций ф, (r) и интегрируется по радиусу лопасти n R                       n R                        nR

Е С , J ( EJ„ Ф" )" Ф k dr - Е С J ( N цб Ф ' )' Ф k dr - Р лхх EJ т л Ф , Ф k dr = 0 ,          (6)

, = 0     0                             , = 0     0                               , = 0 0

где i - номер функции в ряде (5); к - номер функции на которую умножается уравнение (4).

Для вычисляемых интегралов можно ввести обозначение

R

J ( EJ ,, ф") '' ф k dr = с_а

R

J ( N цб ф' ) ' ф k dr = b , к ,                                         (7)

J m л ф , ф k dr = т_й 0

Таким образом, вместо уравнения (4) можно перейти к системе из n алгебраических уравнений вида (6). Система состоит из бесконечного количества уравнений, но на практике целесообразно ограничиться 4-5 членами и, соответственно, 4-5 уравнениями, которые выглядят следующим образом

n

Е С , ( c к - b ,k - Р лх т ,к ) = 0 .                                    (8)

= 0

Форма колебаний в этом случае определяется с точностью до неопределенного множителя с ₀ . Этот множитель может быть найден из условий нормирования. Наиболее распространенное условие нормирования – равенство единице наибольшего отклонения от начального положения. Форма поперечного колебания – это кривая изгиба оси балки в момент наибольшего отклонения от нейтрального положения. При собственных колебаниях внешняя сила отсутствует, поэтому амплитуду колебаний определить невозможно, что и выражается в виде множителя с ₀ .

При расчетах ряд (5) искусственно обрывают [1]. Ввиду этого, величины р и ^. являются приближенными, зависящими от количества членов ряда. С повышением использования количества членов ряда точность расчетов растет.

Преобразованный вид формул для частот собственных колебаний дает следующее решение

P2k = ” + $« — , mkk      mkk где

R m kk = J m ^ k dr , 0

R bkk =J s (^k )2 dr; 0

R

C kk = J Е_л1_Л х ( ^ k )² dr , 0

R

S _л = J ^m _л rdr .

r

В случае если юнв = 0, то вращение не происходит, т.е. квадрат частоты собственных ко- лебаний невращающейся лопасти определяется по формуле pk =    = pL.(10)

mkk

Для упрощения можно ввести коэффициент kk = b-.(11)

m kk

Соответственно формула (9) преобразуется к виду

P\ = Р^т + kkю2т .

Таким образом, собственные частоты колебаний лопасти можно определить, суммируя частоту собственных колебаний невращющейся лопасти и изменение частоты, вызванное увеличением жесткости вследствие центробежной силы. Такой подход пригоден для определения собственных частот колебаний лопасти. Коэффициенты mkk , bkk , ckk вычисляются по формам собст- венных колебаний невращающейся лопасти, также как Pквт . Согласно [1], данный метод может обеспечить погрешность 1-2%.

Выражение (12) показывает, что с ростом угловой скорости ветротурбины собственные частоты изгибных колебаний лопасти повышаются. Физически это объясняется действием растущей центробежной силы, стремящейся распрямить лопасть, т.е. увеличить ее жесткость на изгиб. Как известно, при повышении жесткости собственные частоты колебаний растут.

Уравнение собственных колебаний невращающейся лопасти вытекает из уравнения (1) с учетом отсутствия центробежной силы

(EIП'- Р2„тл^ = 0 .(13)

При незначительном изменении удельной массы и жесткости по длине лопасти уравнение принимает вид

^IV —«4Л = 0 ,(14)

где а _л

= pm

Е л 1 лх .

Общее решение данного уравнения, выраженное через функции Крылова, имеет вид

^( r) = AS (ar) + BT (а r) + CU (ar) + DU (ar),(15)

где A, B, C, D - постоянные, определенные граничными условиями; S, T , U , V - функции Крылова

S( a r ) = 0,5(ch a r + cos a r )

T ( a r ) = 0,5(sh a r + sin a r )

U ( a r ) = 0,5(ch a r - cos a r )

V ( a r ) = 0,5(sh a r - sin a r )

При r = 0, S(0) = 1, а T(0) = V(0) = U(0) = 0. Производные от одной из функция Крылова выражаются через другие:

dS . / d ,    . d

— = 0,51 —ch ar +—cos a dr ^ dr dr dT A / d .    . d ■

— = 0,5 1 —sh a r +—sin a dr I dr dr

.^ = 0,5 a ( sh a r - sin a r ) = a V ,

= 0,5 a ( ch a r + cos a r ) = a S ,

d ² S

d ² S    dV

—- = a— = a U . dr ² dr

Таким образом, любая производная функции может быть найдена путем круговой замены.

Для определения постоянных A, B, C, D используют четыре граничные условия [4]. Из (14) поочередно находятся производные и подставляются в соотношения при r=0 и r=R. Это дает систему уравнений относительно неизвестных A, B, C, D. Такая система имеет нетривиальное решение. Тривиальное решение A=B=C=D=0 отвечает только состоянию покоя лопасти и не представляет интереса. Для нахождения нетривиального решения определитель, составленный из коэффициентов при неизвестных A, B, C, D, приравнивается к нулю. Так получают уравнение для нахождения ai, каждому корню которого соответствует свое нетривиальное решение исходной системы алгебраических уравнений. Подставляя последовательно каждое значение ai в систему алгебраических уравнений, определяются соотношения между коэффициентами A, B, C, D, т.е. соответствующую форму колебаний. Число собственных колебаний балок бесконечно, однако практический интерес представляет собой три-четыре значения ai.

Таким образом, частоты равны

P =a ²

E л I m _л

Приравняв определитель к нулю, получаем выражение для нахождения a _i

Его решения равны

ch( a R ) • cos( a R ) + 1 = 0 .                                  (19) 1,571 a, =        , 1 R 4,712 a 2 =        , R                                        (20) 7,854 a 3 = R ’ 10,996 a 4 = R "

Значение a i может быть определено приближенно по формуле

a »n ^—0,5 .                                (21) i R

Эта формула тем точнее, чем выше номер тона i .

Определение форм колебаний производится с учетом граничных условий винта

^ ( r ) = C

U ( a r )

S ( a r )V ^R ) T ( a R )   ,

Для построения форм колебаний целесообразно воспользоваться условиями нормирования, в частности, равенства величины перемещения конца лопасти единице:

R

К R) = 1, J^( r) dr = 1.(23)

Соответственно производные равны

^' ( r ) = B a 5 + C a T + D a U

^( r) = B a2V + Ca2 S + Da2 T          ,(24)

^'' (0) = Ba² V (0) + C a ² S (0) + D a ² T (0) = C a ² - 1 = 0

Приведенная масса может быть выражена

RR m^ = J m^dr = mJ ^dr = mA,(25)

где A = J ^dr .

Численное интегрирование можно выполнить методом Симпсона:

A _ А r ( C , + 4 C ₂ + 2 C ₃ + 4 C ₄ + 2 C ₅ + ... + C ,, )

_                            3,

Для вычисления b j предварительно необходимо найти квадрат первой производной собственной формы колебаний:

RRR R bj = J (J mrdr)(^>‘H )2 dr = J m(J rdr)(^'jh )2 dr,(27)

0 r                             0

где C i = ^ ² , А r - расстояние между расчетными сечениями лопасти.

Резонансные параметры лопасти. На основании представленной методики был запрограммирован расчет колебаний лопастей малогабаритной ветроэнергетической установки, разрабатываемой ООО «Персональные энергосистемы» (г. Ростов-на-Дону). Внешний вид установки представлен на рис.1. В расчете рассматривалась лопасть радиусом 2,25 м со стальным трубчатым лонжероном с жесткой заделкой в комле. Трубчатый лонжерон выполнял роль несущего элемента. К лонжерону крепился пенопластовый заполнитель с обшивкой. Согласно аэродинамическому расчету оптимальная частота вращения составила 380 об/мин. Расчет велся до частоты вращения 420 об/мин. Интегрирование проводилось вдоль лопасти с шагом 0,1R.

На рис.2 показаны расчетные формы первых трех тонов колебаний лопасти, приведенные по условию нормирования к 1.

Рис.1. Внешний вид малогабаритной ветроэнергетической установки

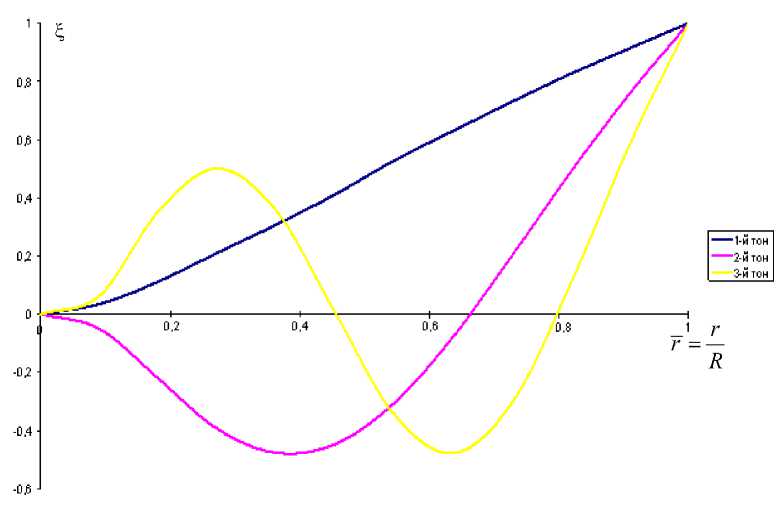
Рис.2. Формы собственных изгибных колебаний лопасти ветротурбины

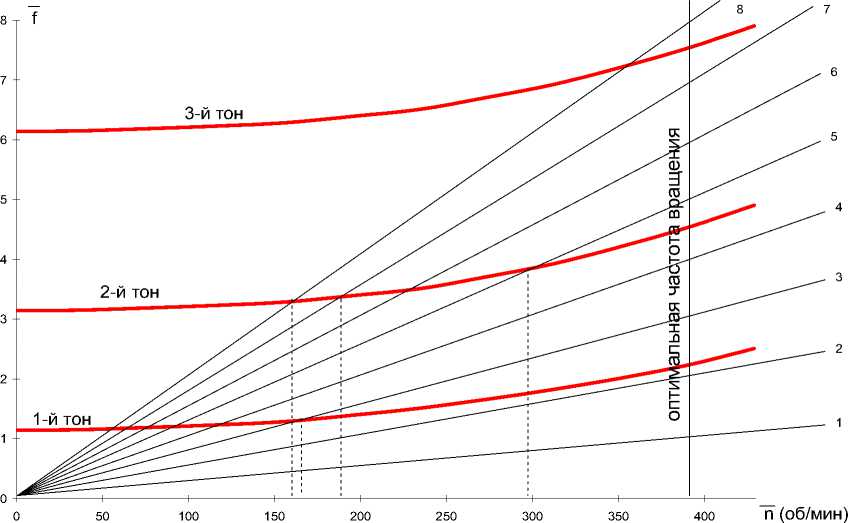
Рис.3. Резонансная диаграмма лопастей малогабаритной ветроэнергетической установки

Как видно из резонансной диаграммы, представленной на рис.3, лопасти имеют хорошие резонансные характеристики, т.е. наступление резонанса возможно только на одной частоте, далекой от оптимальной. Для более наглядного представления значения по оси абсцисс представлены в относительных значениях, приведенных к оптимальной частоте вращения:

p

f = ——, pопт где pопт – оптимальная частота вращения ветроколеса.

На данном рисунке кривые тонов колебаний представляют собой графики собственных частот колебаний лопасти при увеличении центробежной силы. Наклонные прямые – графики частот вынужденных колебаний при различной частоте вращения ветроколеса при разных скоростях ветра. На рисунке видно, что первый тон собственных колебаний имеет низкие резонансные частоты, что характерно для всех ветротурбин, у которых лопасти имеют большой удельный вес и низкую жесткость. Пересечение первого тона с гармониками возбуждающей силы на частоте вращения менее 200 об/мин не представляет проблем, так как на этой частоте управление нагрузкой не осуществляется.

Существует проблема с пересечением второго тона с пятой гармоникой на частоте 297 об/мин. Для защиты от возможных колебаний в этой зоне необходимо добавить в алгоритмы управления требования или ослабления нагрузки, с целью выхода ветротурбины на частоты выше 305 об/мин или увеличения, с целью понижения частот вращения ниже 290 об/мин.

Проверить правильность выполнения расчета экспериментально можно, как правило, в одной точке – при отсутствии вращения. В этом случае на лопасти устанавливается виброгенератор малой массы и производится замер частоты появления резонанса по резкому росту амплитуды колебаний. Создать распределенное усилие, аналогичное нагрузкам на ветроколесе при вращении и сгенерировать колебания для нахождения резонансов представляется проблематичным. Выводы. Таким образом, представленный метод может быть использован для определения резонансных характеристик лопасти ветроустановок, имеющих малое изменение массы и жесткости вдоль лопасти.

Расчет, выполненный для двухлопастной ветротурбины диаметром 4,5 м, показал, что не допустить появления резонанса на данном типе лопастей можно, использовав в алгоритмах управления нагрузкой ограничения рабочего диапазона частот 200-290 об/мин и 305-420 об/мин. Библиографический список

• 1.    Кирпикин А.А. Приближенный расчет резонансных диаграмм несущих винтов вертолетов / А.А. Кирпикин. – Харьков: ХАИ, 1999. – 64 с.

• 2.    Миль М.Л. Вертолеты. Расчет и проектирование / М.Л. Миль [и др.]. – Т.2. Колебания и динамическая прочность. – М.: Машиностроение, 1967. – 424 с.

• 3.    Михеев Р.А. Расчет вертолета на прочность. Прочность лопастей несущего винта / Р.А. Михеев. – М.: МАИ, 1973. – 205 с.

• 4.    Скопинцев Б.И. Собственные колебания лопасти вертолета / Б.И. Скопинцев. – Харьков: ХАИ, 1983. – 200 с.

Материал поступил в редакцию 22.06.2011.