Определение шероховатости поверхности дорожек качения приборных подшипников с использованием квазиоптимального корреляционного алгоритма

Качество поверхности дорожек качения приборных подшипников, во многих случаях является определяющим фактором, влияющим на долговечность и надежность при их эксплуатации.

В настоящее время оценку параметров микро -рельефа различных поверхностей деталей машин и механизмов во многих случаях выполняют с помощью измерительных оптико-электронных преобразователей, используемых совместно со средствами компьютерной обработки сигналов [1-4]. Эти методы имеют серьезные недостатки. Так, например, в [1,2] требуется использовать источники освещения исследуемой поверхности когерентные как во времени, так и в пространстве. В методах [3,4] требуется применение двух световых потоков: первый (опорный) служит для освещения исследуемой поверхности, а второй для компенсации флуктуаций мощности опорного потока, что существенно усложняет контрольноизмерительную аппаратуру данного назначения и её использование на рабочем месте .

Устранения отмеченных недостатков было выполнено с использованием оптико-электронного комплекса [5,6], который включал в себя оптическую систему, видеокамеру, компьютер и специально разработанный алгоритм обработки изображения исследуемой поверхности. Для устранения погрешностей оптико-электронный комплекс авторами работы [7] был рассмотрен как структура информационно-измерительной системы (ИИС), которая состоит из выделенной площади ВП исследуемой части поверхности, источника опорного светового потока ИСП, видеокамеры ВК и блока цифровой обработки сигналов БЦОС. Систему состоящую из ИСП и ВК рассматривали как оптико-электронный измерительный преобразователь (ИП). Совокуп-ность ИСП и ВП образует канал первичного рель-ефно-оптического преобразования. Входная величи-на, воздействующая на вход оптико-электронного ИП, формируется на исследуемой ВП, в которую входят r - типов элементарных площадок с раз-личным микрорельефом. Её можно представить как среднее

r арифметическое Пц = ^ ап^ П^ , где П^ - i -i=1

тый компонент входной величины преоб-разуемого параметра микрорельефа, например, Ra ; а_п — весовой коэффициент, соответствующий доле элементарных площадок ВП с микрорельефом i -того типового уровня (при общем числе типовых уровней r ). Набор значений { i = 1,..., r } определяется конкретным характером механической обработки ВП.

Выходом ИСП является величина опорного светового потока Ф_о . Её действие на i -тую элементарную площадку ВП вызывает появление соответствующего отраженного светового потока величины Ф_в1■ . Таким образом, каждой i -той элементарной площадке ВП соответствует, во-первых, один из выходов канала первичного рельефно-оптического преобразования - величина Ф_вi , воздействующая, в свою очередь на входы ПЗС-матрицы, и, во-вторых, определенный электрический сигнал U_3i ПЗС-матрицы.

Номинальную функцию преобразования i -того компонента входной величины Пц для ИП указан- ного типа, соответствующего i -тому подмножеству одинаково    обработанных    элементов    ВП представляли как

U        ∗           ∗∗ эiн      фэ      вiн       фэ      он         вiн     он

(IX * Ф )* Y = (1Х * Ф )* f (П Л фэ      он      вiн       фэ      он            µi

П

µ i m in

< П p i <  П ^ max ,

где Кф3- коэффициент физического преобразования светового потока Фе/Н в электрический сигнал U3iH ПЗС-матрицы, который в используемых диапазонах изменений измеряемой величины П^ и опорного светового потока Ф„ от них не зависит; Ф„ -o                                      он номинальное значение величины  Ф„; Ф- „ - o          вiн номинальное значение отражённого  светового потока Ф81■, поступающего от любого элемента из i -того подмножества площадок ВП; П ^mn , ПMimax -границы используемого диапазона изменений П и ; f (П^)   - функциональная зависимость номинальных значе-ний нормированного выхода канала     первичного     рельефно-оптического преобразования   Y6iH   от i -того компонента измеряемой величины П м , а Y8iH - характеризует отражательную способность i -того компонента ВП при воздействии на ВП номинального опорного светового потока Фон. Для конкретных образцов, приведенных на рис.4,

П = Ra = 0,025 мкм П _х = Ra = 0,13 мкм. µ i m in                          µ max

Саму же функцию f ( П ^ ) аппроксимировали

m полиномом степени m : f„ (П,„)= / ап * П p , ап     µi          р      µi p=0

где а _р - степенной коэффициент аппроксимации.

При исследовании влияния мощности опорного светового потока на характеристики видеосигнала в работе [7] участок анализируемой поверхности размером L1 x L 2 считывался по строкам и столбцам строчно-кадровым растром черно-белой телевизионной передающей камерой с ПЗС–матрицей и аналогово-цифровым преобразователем, а в запоминающем устройстве БЦОС формировался кадр исходного полутонового изображения поверхности формата К_х х К₂ точек дискретизации - пик-селей. Сигнал яркости каждого пикселя принимал значения, лежащие в диапазоне 0 - 255 от. ед.

За номинальное значение опорного светового потока была принята величина Фон=600 *10-3 лм, а для величин Фошь, Фошах - значения 200*10-3 лм и 1000 *10-3    лм соответственно. Все непредусмотренные воздействия на освещенность исследуемой поверхности можно охарактеризовать с помощью функции влияния согласно ГОСТ 8.009 -  72 “Нормируемые метрологические характе ристики. Средства измерения”. Проведенными исследованиями, выполненными в работе [7], было установлено, что функция влияния носит мультипликативный характер.

Наличие мультипликативного характера функции fg,, ( А Ф ), содержащейся в выражении выходной электрической величины оптико-электронного ИП, диктует выбор логометрического способа устранения рассматриваемой дополнительной погрешности [8]. Однако традиционное применение лого-метрирования предусматривает ведение в состав ИИС дополнительного осветительного канала и второй ПЗС-матрицы, содержащих компенсационные величины, что существенно усложняет и увеличивает габариты ИИС.

Применительно к используемой разновидности измерительного преобразования в [7] был выдвинут новый принцип коррекции дополнительной погрешности, вызываемый нестабильностью опорного светового потока в форме требования соблюдения однозначных соответствий между набором величин ( Y₃ ,( X ^ ), i =1,..., r ), и двумя функционалами G_x ( Y_3i ( X ^ ), i =1,., r ), x =1,2, множества значений которых связываются с измеряемыми и влияющими величинами.

При реализации частного

G 1 ( Y 3. ( X „ ), i =1,., r )/ G 2 ( Y 3. ( X _A i ), i =1,., r ) (1) одинаковые мультипликативные компоненты числителя и знаменателя f^ (п ) сокращаются, что не ведёт к увеличению габаритов создаваемой ИИС.

Реализация предлагаемого способа коррекции дополнительной погрешности в предлагаемой работе была осуществлена с привлечением теории оптимальной линейной фильтрация сигналов известной формы [9], на основе известных методов цифровой обработки сигналов [10,11] по известным гостовским методикам [12]. При сравнении определяется, какой образцовой поверхностью с заданной вероятностью распознавания соответствует исследуемая поверхность, что можно рассматривать как процесс отождествления анализируемого изображения поверхности с одним из элементов множества эталонных изображений с различным микрорельефом. В качестве критерия сравнения неизвестной шероховатости исследуемой поверхности с шероховатостями эталонных поверхностей в работе [7] был предложен коэффициент корреляции, вычисляемый по классической формуле (2) [10] по полутоновому изображению исследуемой поверхности, предварительно записанного в память БЦОС.

N i - 1 N ₂ - 1

r xu ^{( k}1 ,k 2 ) =

E E ^{( u (} n 1 ,n 2 ) ^- m u ) * /вл ^{( A} Ф) * ⁽ x ^{( n} 1 ^- k 1 , n 2 ^{- k} 2 ) ^- m x ) * f вл ^{( A} ФФ) n i = 0 n 2 = 0

^ 1 * /вл ^{( A} Ф) * ^ 2 * f вл ^{( A} Ф )

Используемую автокорреляционную функцию можно рассматривать как частный случай поскольку она обладает искомым компенсационным свойством, не требуя при этом введения дополнительной аппаратуры.

Для вычисления двумерной автокорреляционной функции в кадре, формата K1 х K2 точек дискретизации [5 - 7], начиная с первой стро-ки, выделялась полоса шириной N пикселя и по центру этой полосы задавался эталон (ЭИ) размером N х N пикселей и записывался в отдельную область памяти БЦОС. Найденные значения rц(k, k2) сохраняют в памяти БЦОС. Закончив вычисление  коэффициентов автокорреляции в первой полосе, задавалась следующая полоса того же формата в исходном изображении, что и предыдущая, но смещённая вниз на один пиксель. В этой полосе по центру задавался новый эталон, но с теми же размерами что и предыдущий, и выполняются те же самые действия для вычисления коэффициента автокорреляции и.т.д. Обработка всего кадра исходного изображения по отмеченной методике, в запоминающем устройстве БЦОС формирует матрицу, размерностью Мх х М^ коэффициенты автокорреляции или двумерную дискретную автокорреляционную функцию. Проведёнными исследованиями в работе [7] было установлено, что по средней амплитуде UСР переменной составляющей автокорреляционной функции Г(kk,k2) исследуемые поверхности с различной шероховатостью существенно отличаются друг от друга при всех указанных размерах эталона Существенным недостатком предложенной методики определения шероховатости на основе вычисления коэффициента корреляции по классической формуле (2) с использованием полутоновых изображений является слишком большое время, затрачиваемое на его вычисление. Так, например, при использовании персональной ЭВМ с процессором Intel(R) Core (TM) 2 CPU 4300 @ 1.80GHz, время, затрачиваемое на это вычисление, составляет 160000 мс при использовании эталона с форматом 64×64 пикселя, что    практически  исключает использование данного метода для оперативного контроля качества  поверхности в  производ ственных условиях.

Для устранения этого основного недостатка в предлагаемой работе были рассмотрены квазиопти-мальные алгоритмы для вычисления критериальных функций [13 - 19]: к которым и относится рассмотренная выше двумерная автокорреляционная функция. В приведённых работах отмечается, что сущес-

• 1)    выбор вида предварительной обработки изображения;

• 2)    определение критериальной функции;

• 3)    определение способа поиска экстремума критериальной функции.

Для определения микрогеометрии исследуемой поверхности третий этап не является целью и поэтому в дальнейшем не рассматривается.

Полный перечень требований, которым должны удовлетворять критериальные функции, рассмотрен в [15, 16].

Анализ, выполненный в [16, 17], позволил выделить пять групп критериальных функций со сходными свойствами: корреляционные, спектральные, разностные, парные и ранговые.

Разработку квазиоптимального коре-ляционного алгоритма применим для исследования шероховатости дорожки качения внутреннего кольца приборного подшипника № 2000083 изготовленного из стали ШХ-15 HRC 62….65.

Шлифование дорожки качения внутреннего кольца подшипника осуществляялось на оборудовании Bryant 1-M с режимами: частота вращения шпинделя – n_к =1750….1850 об/мин; коэффициент полез-ного действия – ή =0,8; размеры шлифовального круга – D к =355 мм, В к =16 мм; приме-няемый АК для черновой обработки – 24АМ40СТ1К; правка круга – поперечная подача S_поп = 0,015 мм /дв.ход, продольная подача S пр = 0,02 мм/об, минутная подача S_м и _н= S п _P х п_о= 0,02 х 1850 = 37 мм/мин, алмаз в оправе α= 90⁰, время правки τ=15 с.

Параметры исследовательского оптикоэлектронного комплекса были настроены таким образом, чтобы уменьшить влияние кривизны исследуемой поверхности на её изображение в фокальной плоскости оптической системы: в данном случае участок анализируемой поверхности имел размер 1,2 х 1 мм, а формат записываемого в память компьютера изображения составлял 720 х 576 пикселей. В связи с выявленными особенностями, опорный световой поток при исследовании шероховатости дорожки качения был направлен вдоль дорожки и под большим углом - а = 70⁰. Изображения поверхностей эталонных образцов формата 720 х 576 пикселей. Шероховатость эталонных образцов определялось традиционными гостовскими методами при помощи профилографа SJ – 201P.

Поскольку в настоящее время не существует [15, 16] формального способа выбор вида предварительной обработки и типа критериальной функции производили эвристически. На основе проведённого анализа были выбраны парные критериальные функции, которые предполагают обработку изображений в цифровой форме с числом уровней квантования два и более.

При этом наиболее употребляемые парные критерииальные функции [18,19] это: функции Рао, Дже-карда, Дейка, Соукала и Снита, Кулзинского, Род-жерса и Танимото №1 и №2, Соукала и

Мишнера, Юла, Хаммана.

С помощью метода парных критерии-альных функций может быть получено несколько кореляционно - экстремальных алгоритмов. В выполненной работе был выбран алгоритм, построенный с использованием парной критерииальной функции, в виде R_T ( А ) =

|  2 n ^{- 1}

— У F ( А ) , где N - количество сравниваемых Nf₀

элементов в ЭИ и ТИ.

Бинаризация исходного полутонового изображения проводилась по следующему алгоритму. Всё исходное изображение исследуемой поверхности разбивалось на независимые квадратные фрагменты (окна) и в каждом окне подсчитывался средний уровень яркости видеосигнала Вт (x, у) . Этот средний уровень и являлся порогом бинарного преобразования для яркости пикселей в данном окне, то есть скользящим порогом [20]. В выделенном окне преобразовывался каждый пиксель, а перемещение окна по преобразуемому изображению осуществляется с шагом, определяемым размерами окна. Отмеченное преобразование использует все три вида фильтрации изображения, то есть каузальную, некаузальную и полу- каузальную фильтрации. В результате сравнения каждого байта Bi (x, у) с пороговым значением ВТ (x, у) ему придавалось новое значение по правилу: В A x, у ) = 0FFH, если В Ax,у) > Вт(x,у) и В Ax,у) = 00H, если

В ^{( x} , У ) <  В Т ( x , у ) . Такой формат бинарного изображения был выбран для того, чтобы обеспечить возможность его обработки языками высокого уровня и вывода результатов обработки на экран монитора ПЭВМ. На рис. 1 приведены бинарные изображения эталонных образцов, полученные при использовании адаптивного окна бинарного преобразования с размерами 16x16 пикселей.

Принципиальное отличие нового метода определения двумерной автокорреляционной функции заключается в способе её вычисления по квазиоп-тимальному корреляционному алгоритму на основе применения парных критериальных функций F ! ( А) и F _{o 0} (А) , а не по классическому методу при использовании квазиоптимального корреляционного алгоритма по подсчету количества совпавших пикселей S в текущем фрагменте бинарного изоб-ражения В_т и эталоне В_э . Для получения норми-рованного значения этой суммы она делится на размер эталона, то есть на то значение суммы, которое получается при полном совпадении эталона и текущего фрагмента бинарного изображения.

Таким образом, этой нормированной сумме с полным основанием можно придать смысловое значение коэффициента кор-реляции rx(kkx,к2) , так как она отвечает всем требованиям стохастической связи, приведенными в [16, 17], в частности 0 < r(kк,,k2) < 1. При использовании данного метода также компенсируется дополнительная погрешность, возникающая в результате воздействия фун- кции влияния f^ (АФ, А а) в связи с тем, что в точке совпадения значений пикселей эталона Вэ и выделенного фрагмента текущего бинарного изоб-

Ra =0,13 мкм Ra =0,084 мкм Ra =0,048 мкм Ra =0,025 мкм

Рис. 1. Бинарные изображения поверхностей эталонных образцов.

бражения В_т она будет умножаться на ноль, то есть

АВ = ВТ X fвл (АФ, Аа) - ВЭ X fвл (АФ, Аа) = fвл (АФ, Аа)X (Вт - Вэ) = f вл (АФ, Аа) X 0 при Вт = Вэ .

Кроме того, только в этой точке наращивается, отмеченная выше сумма Sx= Sx +1, то есть мера корреляции эталона и текущего фрагмента изобра- жения, согласно алгоритму применения парных крите-риальных функций Fvt (А) и Рй,0 (А) .

Для микрорельефа рассматриваемых поверхностей с помощью оптико-электронного комплекса, в работе были выполнены исследования влияния шероховатости поверхности эталонных образцов на среднюю амплитуду переменной составляющей авто-корреляционной функции Ra = f ( U_ср ).

Для каждого образца также было обработано по 30 изображений с различных участков исследуемой поверхности, то есть n = 30 и СКО оценки при определении U _ср определялось по формуле [21].

с

Ct = Т n

При этом формат эталона и размер окна бинарного преобразования для выполненных исследований составлял 16 х 16 пикселей.

Следовательно, задавая вероятность распознавания шероховатости исследуемой поверхности Р =0,99 и t р = 2,576, для образцов поверхности с

Ra = 0,13 мкм имеем ^с t = 0,31 мкм, для образцов с

Ra = 0,084 мкм имеем Ct = 0,24 мкм, для образцов с Ra =0,048 мкм имеем ct = 0,15 мкм и для образцов с Ra = 0,025 мкм имеем ct =0,018 мкм. Используя выражение для доверительного интервала [21] Iв = (Uср — tр х с t ; Uср +1р х с t ) получим следующие величины доверительных интервалов:

Ra = 0,13 мкм - I р = 0,8 отн. ед. 15,2 отн.

ед.< U_СР < 16,8 отн. ед.;

Ra = 0,084 мкм - I р = 0,6 отн. ед.

11,6 отн. ед.< U_СР < 12,8 отн. ед.;

Ra = 0,048 мкм - I р = 0,4 отн. ед.

• 9,5 отн. ед.< U_cР < 10,3 отн. ед.;

Ra = 0,025 мкм - I р = 0,05 отн. ед.

7,81 отн. ед.< U_cР < 7,91 отн. ед.

График зависимости I р = f (U _ср} для формата изображения исследуемой поверхности 720 х 76 пикселей приведён на рис. 2. Как видно из приведённых данных доверительные интервалы для U_СР с увеличением шероховатости возрастают, но не перекрываются, при этом зависимость I р = f ( U_cр) имеет нелинейный характер. Используя метод наименьших квадратов, для данного доверительного интервала было получено аналитическое выражение в виде

Iр = (0,09 х UcР - 4,2 х UcР2 + 68,5 х х UСР - 314,9) х 10 -2 отн. ед. (3).

Согласно      приведённому     графику, рассматриваемая зависимость Ra = f (UcР) для исследуемых образцов имеет линейный характер и с помощью метода наименьших квадратов может быть представлена в виде

Ra = 0,0013 х U_cp - 0, 078 мкм      (4)

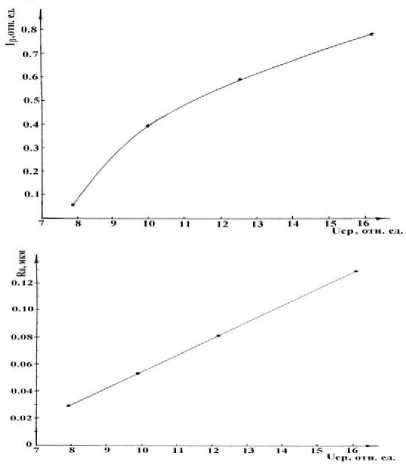
Рис. 2. Зависимость доверительного интервала I р и величины Rа от амплитуды переменной составляющей автокорреляционной функции U_сР .

При исследовании поверхности очень важно определить наличие различных дефектов на дорожки качения, которые ввиду своей малой величины не фиксируются контролерами ОТК. Визуальные исследования дорожек качения с помощью оптико-электронного комплекса показали, что на её поверхности образуются дефекты в виде рисок и точек, которые встречаются у 95% колец обработанных на шлифовальных станках марки Bryant 1M с применением масляной СОЖ. Риски, как правило, разнонаправленные, что говорит о случайном процессе их образования.

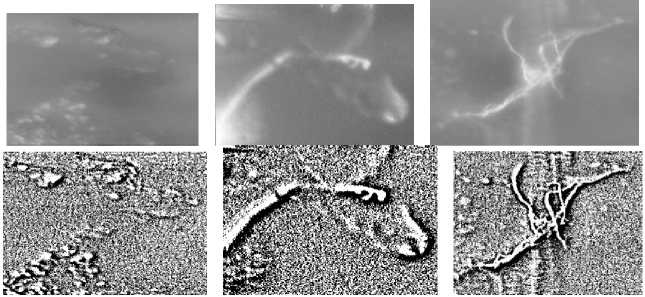
На рис.3 приведены полутоновые и бинарные изображения типичных дефектов на участках поверхности дорожки качения внутренних колец приборных подшипников № 2000083 после операции шлифования с применением масляной СОЖ.

Ввиду сильной кривизны дорожки качения максимальный формат анализируемых участков поверхности не превосходил значения 450 х 400 пикселей из общего формата 720 х 576 пикселей, формируемого в памяти компьютера оптикоэлектронного комплекса.

Из 30 колец, которые были исследованы, на 27 кольцах обнаружены дефекты (90%).

Важно знать глубину этих дефектов. Анализ приведенных данных показал, что в местах образования повреждений дорожки качения (дефектов) наблюдается возрастание амплитуды переменной составляющей автокорреляционной функции.

Измерения глубины дефектов дали следующие значения: для участка №1 U =12,5 отн. ед., для участка №2 U _СР =14,34 отн. ед., для участка №3 U _СР = 14.3 отн. ед.

Подстановка этих значений в выражения (3) и (4) дала следующие результаты для среднего арифметического отклонения профиля поверхности дорожки качения в повреждённых местах:

участок №1 - I в = 0,6 отн. ед.;

Ra min = 0,077 мкм , Ra max = 0,092 мкм , участок №2 - Iр = 0,7 отн. ед.;

Ra = 0,099 мкм , Ra = 0,117 мкм , min                    m ax участок №3 - Iр =0,69 отн. ед.;

Ra = 0,098 мкм , Ra = 0,116 мкм . min                    m ax

При общей высоте шероховатости равной 0.24 мкм дефекты соизмеримы с общим фоном и контролерам не удается их обнаружить.

Исследования дорожки качения оптико-электронным комплексом показали, что после шлифования колец с водной СОЖ количество и глубина дефектов значительно уменьшилось до 0.05-0.07 мкм. На рис. 4. приведены полутоновые и бинар- ные изображения участка дорожки качения после

№1            №2            №3

шлифования с водяной СОЖ, а также график изменения коэффициента корреляции и автокорреляционная поверхность.

Амплитуда переменной составляющей автокорреляционной функции в этом случае имела значение U = 7,9 отн. ед. Следовательно, доверительный интервал согласно выражению (3) составил 0,09 отн. ед. и среднее арифметическое отклонение профиля поверхности дорожки качения при использовании выражения (4) находится в диапазоне Ra_m = 0,024…0,026 мкм, что вполне отвечает требуемым техническим условиям.

Применением полирования шероховатость, была снижена до уровня Ra = 0,018 - 0,19 мкм .

На основе полученной информации был разработан и внедрён в производство процесс шлифования дорожек качения в среде водных СОЖ, что позволило резко снизить процент брака на данной технологической операции.

В заключении данной работы можно также отметить, что на рассмотренный оптико-электронный комплекс и способ определения шероховатости исследуемой поверхности на его основе получен патент Российской Федерации № 2413179 “Способ контроля шероховатости поверхности.”

Рис. 3. Изображения дефектов на участках дорожек качения внутренних колец приборного подшипника № 2000083 после операции шлифования с применением масляной СОЖ

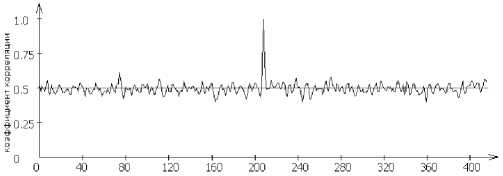
пиксели

Рис. 4. Полутоновое и бинарное изображения дорожки качения подшипника после шлифования с водной СОЖ, автокорреляционная поверхность и график автокорреляционной функции.