Определение ширины плотности распределения энергии электронного пучка по его сечению при электронно-лучевой сварке

Существуют различные способы экспериментального определения диаметра электронного пучка. Наиболее простым является метод вращающегося зонда [1; 2], сущность которого состоит в том, что тонкий вращающийся зонд, выполненный в виде вольфрамовой проволоки диаметром 0,1 мм, пересекает электронный пучок перпендикулярно его оси и отбирает на себя часть тока. По кривой зондового тока (зондовой характеристике) строят плотность распределения тока электронного пучка по его сечению и вычисляют диаметр. Более точные результаты получают при отклонении пучка на щелевую диафрагму или отверстие малого диаметра, под которым размещен цилиндр Фарадея [3]. Для контроля ширины плотности энергии пучка на поверхности обрабатываемых деталей используют рентгеновский датчик с коллимированной насадкой. Датчик ориентируют на поверхности свариваемых деталей, а для определения геометрических параметров электронный пучок пересекает зону обзора коллимированного датчика.

Расчет диаметра электронного пучка. Диаметр элек тронного пучка рассчитывают по величине оценки ширины плотности распределения тока.

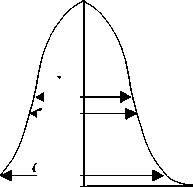
В качестве параметров, характеризующих ширину плотности распределения тока электронного пучка, обычно используют следующие (рис. 1):

• -    ширину кривой распределения, вычисляемую на характерных уровнях ее максимального значения J [4]: d _{0 05} - на уровне 5 % от максимальной амплитуды J _тах ; d ₀₅ - на уровне 50 % от максимальной амплитуды J _тах ; d - на уровне 1/ е от максимальной амплитуды J ;

• -    ширину равномерной плотности распределения (ее площадь равна площади, охватываемой кривой распределения), нормированную максимальным значением величины плотности распределения J [5]:

1 го d s = — j jп (x) dx .

max -^

Если плотность распределена по нормальному закону, то ds = J— = сп V2n = 2,5сп, где сп - среднее квадрати ческое отклонение электронов от оси электронного пучка, которое определяют по второму центральному моменту ц2 ∞ функции распределения: ц2 (x) = сП (x) = j x2 jп (x)dx;

• -    ширину интервала, равную двум средним квадратическим отклонениям электронов от оси электронного

  4 Jn ( x )

  J max

  

  , d Q.5

  d.

  d 0.05

  
  
  

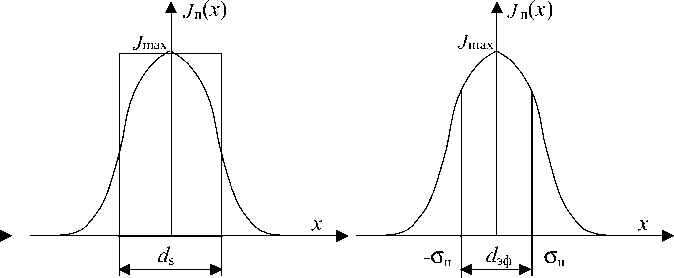
  Рис. 1. Способы определения геометрических параметров электронного пучка

  
  

пучка, обычно называемую эффективным диаметром; d _зф = 2 о _п . В случае распределения плотности энергии по нормальному закону d _зф указывает интервал, в который попадает 68 % энергии электронного пучка.

Энтропийная оценка ширины плотности распределения тока пучка. Следует отметить, что существующие оценки не учитывают форму кривой распределения или рассчитываются исходя из условия, что плотность распределена по нормальному закону Реально существующие распределения могут отличаться от нормального закона. Установлено, что на геометрию пучка влияют изменение ускоряющего напряжения и тока. На форму распределения также влияют различные дефекты катода, изменение давления в вакуумной камере. Наличие разнообразных факторов, влияющих на плотность распределения энергии пучка, приводит к тому, что однозначного соотношения между средним квадратическим отклонением О _п и диаметром электронного пучка d как энергетической оценкой вносимой удельной мощности q ₂ нет Для коррекции этой неоднозначности необходимо вводить поправочные коэффициенты, учитывающие вид закона распределения.

В качестве параметра, учитывающего закон плотности распределения энергии, для оценки ширины распределения можно использовать энтропию [6] м

H ⁽ x ) = ^— J j п ⁽ x ) ¹ⁿ⁽ j п ⁽ x )) dx .

Энтропия является функционалом закона плотности распределения энергии и учитывает особенности этого закона. Численное значение энтропии и ее связь со средним квадратическим отклонением могут быть получены для различных законов распределения (рис. 2).

а

^Аj п ( X )

б

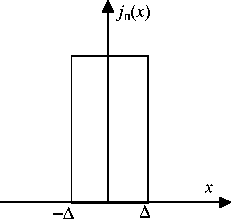
Рис. 2. Законы распределения: а - равномерный; б - нормальный

Закон равномерного распределения энергии (рис. 2, а) определяется по формуле jп ( x) = -

2 Д при] x < ^Д .

k 5

0 при| x > Д .

Значение энтропии равномерного распределения будет равно

Д 1.1.

H ( x ) = —[ —ln — dx = 1п2 Д .       (1)

^р _-Д 2 Д 2 Д                      ^v '

Дисперсия равномерного распределения

м

Д

п

2 1 ,     Д '

x —dx =—

2 Д      3

—м               —Д

Отсюда энтропию можно выразить по среднему квад- ратическому отклонению:

H _р ( x ) = 1п ( 2Т3 О п ) .

Закон нормального распределения (рис. 2, б) имеет вид

² x ^{2 2 —} 20"

j п ^{( x} ) = /л~ exP V 2 по _п

Значение энтропии для этого закона м

.

dx =

H „ ^{( x} ) = J j п ^{( x} ) ^1п ( V²^ ) ⁺ 2^4 _—

• —м        у                      п у

• м              1 м

• = ^1п (V²^ ) J j п ^{( x} ) ^dx +      J ^{x 2} j п ^{( x} ) ^dx ,

—м               п —м мм так как J jп (x)dx = 1 и J x2 jп (x)dx = 02, то

—м

—м

^H „ ^{( x} ) = ¹ⁿ ( V2кa п ) + 2 =

= 1n ( 72Пс _и ) + 1n ( 4e ) = 1n (V 2 n e о _п ) .       ⁽²⁾

При практическом использовании изложенного под- хода для оценки геометрических параметров электронного пучка привычнее оперировать не значениями энтропии, а шириной плотности распределения.

^в

Для энтропийной оценки ширины плотности распределения можно выбрать ширину равномерной плотности распределения, энтропия которой равна энтропии плотности измеряемого распределения. Эту оценку назавем энтропийным диаметром электронного пучка и обозначим d .

Произведем расчет энтропийного диаметра для случая нормального распределения тока электронного пучка. Для этого приравняем выражения (1) и (2): d ₃ = 2 Д = V 2 п e о _п = 4,13 о _п .

В случае произвольной формы кривой распределе-нияуп(х) = ф(х) значение энтропийного диаметра определяем следующим образом. Найдем значение энтропии м распределения: H(x) = -Jф(x)1nф(x)dx. Приравняем его к выражению (1): 1п2Д = H(x), d3 = 2Д = exp(H(x)).

Энтропийное значение диаметра получается в тех же единицах, в которых измеряется ширина равномерного распределения, согласно соотношению d ₃ = exp( H _р ( x )) = exp ( 1n ( 2 Д ) ) = 2 Д .

Для энтропийной оценки эффективного диаметра выберем интервал, равный двум среднеквадратическим отклонениям нормального закона распределения, энтропия которого равна энтропии плотности измеряемого распределения. Эту оценку назовем эффективным энтропийным диаметром электронного пучка и обозначим d _зфз .

Для его вычисления найдем значение энтропии распределения произвольно й фо рмы Н ( х ) и приравниваем его к выражению (2): 1n (V 2 п e о _п ) = H ( x ) , отсюда следу- 2

ет, что d ._:. = 2 о = .exp H ( x ) .

V 2п е

Учитывая, что значение энтропийного диаметра dэ = exp H(x), зависимость между эффективным энтропийным диаметром и энтропийным диаметром имеет вид dзф.э = -/T=dз = 0,484dз ■

2 п e

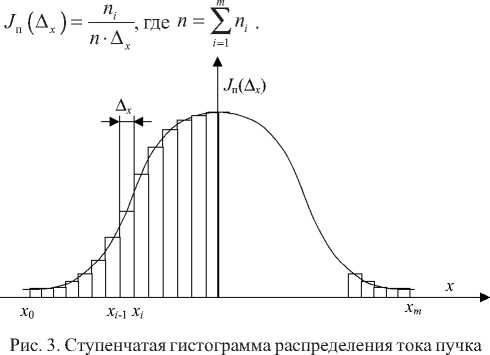
Расчет энтропийного диаметра по зондовым характеристикам. При оценке ширины плотности распределения электронного пучка располагают не самим законом распределения, а набором дискретных величин, подчиняющихся этому закону Это связано с тем, что в процессе измерения плотности электронный луч отклоняется на зонд, щелевую диафрагму или на проекцию коллиматора, которые обладают определенными размерами На основании этого ограниченного числа измерений может быть построена ступенчатая гистограмма, приближающаяся к действительному распределению.

Пусть ступенчатое распределение (рис. 3) состоит из ц столбцов с границами х ₀, х_р х ₂, ..., х , . х _т . Каждый столбец шириной A _x = x i - x i - 1 включает п дискретных результатов измерения. Плотность распределения на протяжении каждого из столбцов остается постоянной и равной

роля плотности распределения энергии электронного

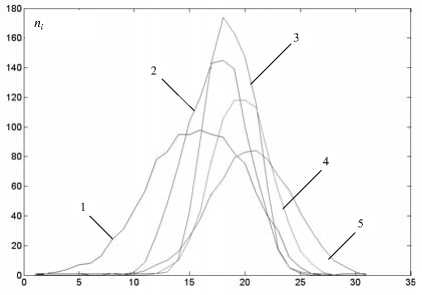
пучка по его сечению [7], представлены на рис 4.

x i • 0,1, мм

Рис. 4. Зондовые характеристики плотности распределения тока электронного пучка, соответствующие различным значениям тока фокусирующей системы: 1 - / _ф = 127 мА; 2- / =129 мА;3- / =132 мА;4- / =134мА;5- / = 136 мА ф                ’ ф                ’ ф                ’ ф

Энтропия такого ступенчатого распределения

“                                     m x i

H = - J j„ ( A _x )ln ( j „ ( A _x ) ) dx = - X J

-*>                                       i = 1 x_M

ni

n -A x

n

In----- dx = n ^-A x

m

=-X

i = 1

n_i n ^-A x

ln

n_i n '^A x

x i

J dx =

^{- x} M

m n , n -A m nn

= X ln---- = X  ln~ + lnAx ■ i=1 n      n      i=1 n n

Можно преобразовать это выражение к виду

Для контроля плотности распределения использовался коллимированный рентгеновский датчик. Датчик располагался таким образом, чтобы проекция коллиматора, представляющая полосу шириной 0,1 мм, располагалась в непосредственной близости от места сварки

Для измерения геометрических параметров распределения тока электронный пучок периодически пересекал проекцию коллиматора. Вычисление значений среднеквадратического отклонения о , энтропийного диаметра d _з и его эффективного значения производилось на основании статистической обработки серий наблюдений Каждая серия состояла из восьми реализаций, в каждой реализации 32 точки Значения показаний датчика в каждой точке измерения усреднялись по всей серии наблю- 1⁸ дений по формуле x = - X x i j ■ ⁸ j = 1 ^,

Перемещение пучка из одной точки в другую соответствует 0,1 мм. Для оценки точности проводимых измерений для каждой серии измерений вычислялись значения энтропийного диаметра d * отдельных реализаций. Затем полученное значение d _з * подвергались статистической обработке. Вычислялось их среднее квадратическое отклонение о ( d _з ) . Интервал доверительной погрешности A ₀,9 ( d _з ) , определяющий интервал для доверительной вероятности Р_Д = 0,9 , рассчитывающийся по выражению [6] A ₀,₉ ( d _з ) = 1,6 о ( d _з * ) .

Относительная погрешность, %, рассчитывалась по

m

H (A x) = ln A x +X ln i=1

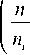
= In

m

A x П

ni n n

ni

A ₀₉ ( d _з ) выражению A ( d ) = —,---- 100 .

d з

Результаты расчетов представлены в таблице.

Тогда энтропийный диаметр будет равен

m dз = exp (H (Ax ))=Ax П i=1

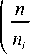
n i

n

/

1 ^m

^- X n lg n i

= A x , ⁿ =A • n - 10 ⁿ =

x

m n П(ni)ni i=1

Зондовые характеристики, полученные экспериментально с помощью автоматизированной системы конт

Таким образом, сделаем следующие выводы:

• -    ширину плотности распределения тока электронного пучка необходимо оценивать параметром, учитывающим форму кривой распределения;

• -    в качестве параметра, учитывающего закон распределения тока, для оценки ширины распределения можно использовать энтропию Н ( х ), ее нелинейный функционал d _з = exp( H ( x )) , называемый энтропийным диаметром и его эффективное значение d _з ф. _з = 0,484 d _з , называемое эффективным энтропийным диаметром.

Параметры распределения плотности пучка

№ серии	Ток фокусирующей системы, мА	а п , мм	d э , мм	d эф.э , мм	А „т„ ( d 3 ), %
1	127	0,424	1,701	0,823	1,8
2	129	0,293	1,162	0,562	6
3	132	0,28	0,953	0,461	8,9
4	134	0,282	1,082	0,524	8,8
5	136	0,72	1,499	0,726	4