Определение сил взаимодействия основных систем геохода с геосредой и между собой

При геоходной проходке подземной выработки происходят одновременные процессы взаимодействия нескольких систем геохода между собой и с геосредой [1-5]. Причем эти процессы взаимо-влияющие [6-9].

Моделирование процессов, происходящих при геоходной проходке подземной выработки, преследует, на наш взгляд, три основные цели[8-14]:

Цель 1 Обоснование параметров приводов и сил возникающих при взаимодействии систем геохода с геосредой и между собой.

Цель 2 Обеспечение достаточной прочности элементов машины.

Цель 3 Обеспечение несущей способности прилегающего (приконтурного) массива горных пород.

Достижение первой цели, кроме того, позволяет сформировать исходные данные для решения задач, преследующих вторую и третью цели. Поэтому рассмотрим именно модель для определения сил взаимодействия систем геохода с геосредой и между собой.

В работах [12-14] обосновывается применение блочно-модульного принципа построения математической модели, что позволит решать частные задачи моделирования работы отдельной системы, используя результаты моделирования работы смежных систем в качестве исходных данных.

Поэтому необходимо абстрагироваться от частных конструктивных особенностей, и упростить задачу, заменив силовые схемы некоторых систем эквивалентными нагрузками и приведенными суммарными моментами и силами.

Для построения обобщенной модели были сделаны следующие допущения и введены приведенные нагрузки:

• 1)    Все силы центрально симметричны относительно оси выработки z .

• 2)    Со стороны главного забоя воздействие геосреды на геоход передается через исполнительный модуль (ИО ГЗ) и может быть приведено к суммарному моменту М_иогз и суммарной силе Р_иогз (рис. 1). Момент М _иогз направлен вокруг

МИСиС

оси выработки z , а сила F    направле на вдоль оси z .

• 3)    Взаимодействие исполнительных органов внешнего движителя (ИО ВД) передается на корпус головной секции и может быть приведено к двум силам: подачи F ^П , направленной вдоль направления подачи на забой канала и лежащей в плоскости, касательной к оболочке корпуса; и резания F ^Р , направленной перпендикулярно к направлению подачи и лежащей в плоскости, касательной к оболочке корпуса. Крутящие моменты от ИО ВД уравновешивают друг друга и могут не учитываться.

• 4)    Взаимодействие исполнительных органов элементов противовращения (ИО ЭП) передается на корпус хвостовой секции и может быть приведено к двум силам:  подачи F ^П , направленной

вдоль направления подачи на забой канала и лежащей в плоскости, касательной к оболочке корпуса; и резания F ^Р , направленной перпендикулярно к направлению подачи и лежащей в плоскости, касательной к оболочке корпуса. Крутящие моменты от ИО ЭП уравновешивают друг друга и могут не учитываться.

• 5)    Взаимодействие лопастей внешнего движителя (ВД) передается на корпус головной секции и может быть приведено к двум силам: нормальной F^N , направленной по нормали к опорной поверхности лопасти и приложенной к точ- ТР ке на основании лопасти; и трения F , приложенной к основанию лопасти и направленной вдоль основания лопасти.

• 6)    Взаимодействие лопастей элементов противовращения (ЭП) передается на корпус хвостовой секции и может быть приведено к двум силам: нормальной F ^N , направленной по нормали к опорной поверхности лопасти и приложенной к точке на основании лопасти; и трения F _Э ^Т _П ^Р , приложенной к основанию лопасти и направленной вдоль основания лопасти.

• 7)    Взаимодействие оболочки головной секции с геосредой может быть при- ТР

ведено к силе трения F , равномерно распределенной по оболочке и направленной параллельно винтовой линии ВД.

• 8)    Взаимодействие оболочки хвостовой секции с геосредой может быть ТР

приведено к силе трения F , равномерно распределенной по оболочке и направленной параллельно оси выработки.

• 9)    Проявление горного давления может быть приведено к нормальной нагрузке p , равномерно распределенной по оболочкам корпусов.

• 10)    Взаимодействие головной и хвостовой секций может быть приведено к суммарному приводному моменту M и суммарной тяговой силе F . Момент M направлен вокруг оси выработки z , а сила F направлена вдоль оси z .

На рисунке 1 показана схема к модели силового взаимодействия основных систем геохода с геосредой и между собой.

На рис. 2 показана схема приведения сил резанья и подачи на ИО ГЗ к суммарному моменту M    и суммар- ной силе F (рис. 1).

Приведенный момент, действующий со стороны забоя, определяли по формуле:

П   ^R В

M иогз   ² ^ иогз 2 ,

где R м – радиус выработки.

Приведенную суммарную силу, действующую со стороны забоя, определим по формуле:

'ИОГЗ = ² F POIB cos ^а ,

Приведенную силу трения, действующую на головную секцию и внешний (вращающийся) корпус модуля сопряжения, определяли по формуле:

F T = Р гд f тр 2 n R c L гс , (3)

где fтр – коэффициент трения металла по породе.

МИСиС

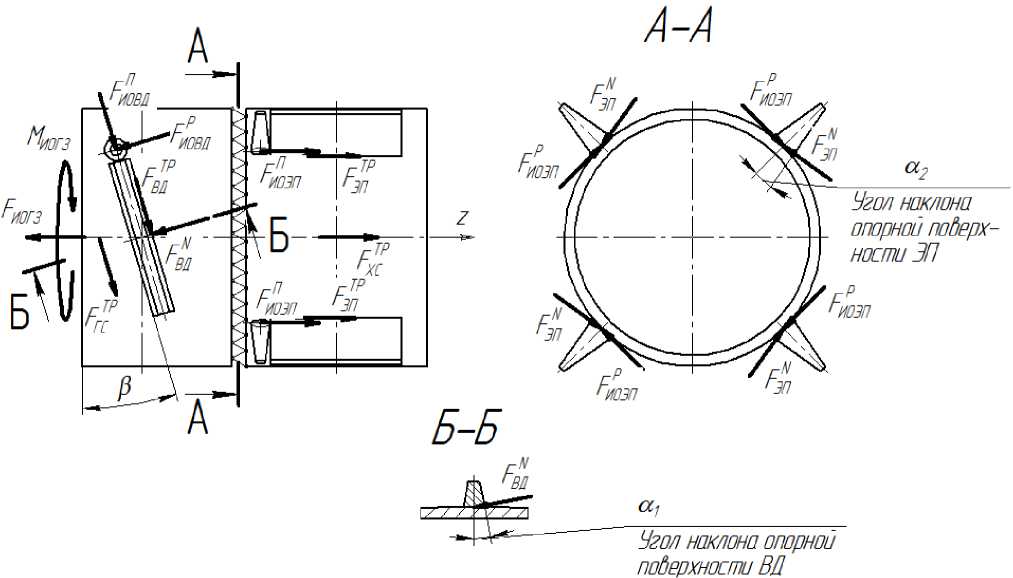
Рис. 1. Схема к модели взаимодействия геохода с геосредой

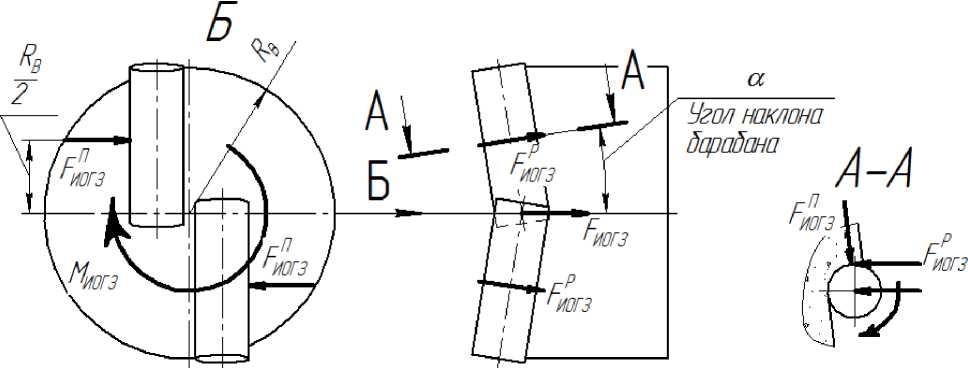
Рис. 2. Силы, действующие на ИО ГЗ со стороны геосреды

Приведенную силу трения, действующую на хвостовую секцию, определяли по формуле:

F xc = p ГД f тр ^{2 n R}C L ХС ,    (4)

Скорость движения геохода достаточно мала и силами инерции можно пренебречь, поэтому сделаем допущение, что геоход движется равномерно и прямолинейно, это позволило составить систему уравнений равновесия.

Уравнение проекций сил на ось z:

2 F Z = F xc + F rc sin P F nor3 + ^{2 F} ИОВД sin P ^{2 F} ИОВД ^cos P +

+ 4 F П  - 2 F X cos P cosa, + 2 F _RТР sin B + 4 F ₄ТР = 0

ИОЭП     ВД           1     ВД          ЭП

Уравнение моментов сил относительно оси z:

МИСиС

^ M z = F rc ^RС cos P + M ИОГЗ + ^{2 F} ИОВД ^RС ^cos P + ^{2 F} ИОВД R C sin P

- 4 FRr + 2 FNR sin В cosa, + 2 F,,ТР Rr cosB-4 FNRr cosa2 = 0 ИОЭП С     ВД С           1     ВД С           ЭП С2

Учитывая, что силы трения пропорциональны нормальным силам:

ТР

F BI f тр F UJ

ТР

ЭП   f тр ЭП уравнения равновесия можно привести к системе:

^Fxc ⁺ F rc ^sin P ^{— F}ИОГЗ ^{+ 2} F HOUJ^sin P ^{— 2} F HOUJ^cos P +

+ 4 F ^ — 2 F UJ (cos p cos a i — f _rp sin P ) — 4 f _rp F э^V_п = 0

F x" cos p — M ^ + 2 F ^ cos p + 2 F^ sin P + ^R c

+ 4 F _И ^P _OЭП + 2 F _UN (sin p cos a 1 + f _rp cos p ) — 4 F ^_n cos a ₂ = 0

Силы, возникающие на исполнительных органах, могут быть предварительно определены исходя из типов исполнительных органов и заданных производительности машины и сечения выработки [15]. То же можно сказать про габаритные размеры геохода и его секций, а также силы проявления горного давления. Значение угла P наклона лопастей ВД лимитируется параметрами ИО ГЗ [2, 3]. То есть определение этих параметров, это частные задачи отдельных блоков, формирующих общую блочно-модульную модель. Значения сил резания и подачи напрямую не зависят от варьируемых геометрических параметров (a_t и a ₂), и их можно рассматривать как константы или независимые переменные.

Из сил, обозначенных на схеме взаимодействия геохода с геосредой (рис. 1), от варьируемых геометрических параметров (at и a2) напрямую зависят только силы, действующие на лопасти N       ТР внешнего движителя ( FN и F ) и элементов противовращения ( F N и F ТР ).

Определение значений сил, возникающих при взаимодействии ВД с геосредой, является частной задачей, которая преследует «цель 1» и позволяет получить исходные данные к задачам, преследующим «цель 2» и «цель 3».

Поэтому рассмотрим частную задачу - определение влияния угла at наклона опорной поверхности ВД на силы взаимодействия геохода с приконтурным массивом. Для этого посчитаем, что угол a2 наклона опорной поверхности ЭП -некая заданная постоянная величина.

Введем константы:

МИСиС

^С1 = F XC + F FC sin Р   F HOF3 + ^{2 F} ИOВД ^sin Р   ^{2 F} ИOВД ^cos P + ^{4 F} ИОЭП ;

С 2 = - 2cos p ;         С 3 = 2, f _ф sin р ;           С 4 = - 4 f _ф;

^С 5 = ^FXC c ^OS P     ИОГЗ + ^{2 F} ИOВД c ^0S P ^{+ 2 F} ИOВД sin Р ^{+ 4 F} ИOЭП^;

R _С

С 6 = 2sin Р ;

С₇ = 2 f _pcos P ;          С ₈=- 4cosa₂

Тогда система уравнений (8) принимает вид:

' С , + F N ( С ₂ cos a i + С з ) + С 4 F N = 0

С 5 + F N ( С 6 cos a i + С 7 ) + С 8 F N = 0

Решая систему, получили:

N

¹ ВД

С С -С с 54  18

( С 2 С 8

- С₆С ₄) • cos a, + С₃С ₈ - С₇ С₄

Введем константы:

A 1

= с С -С с

С 4 С 5   СС 8

A2

= с С -С с

С 2 С 8   С 4 С 6

A3

= СС - СС 47  38

Тогда решение принимает вид:

F N =----- A¹ -----  (11)

A ₂ • cos a, - A₃

Диапазон возможных углов наклона опорной поверхности лопасти ВД определяется условием:

A ₂ • cos a, - A₃ >  0 (12)

Очевидно, что минимальная нагрузка на лопасть будет при радиальном расположении образующей опорной поверхности лопасти ВД, т.е. при а = 0 •

Критическое значение угла наклона

опорной поверхности:

а, 1 кр

/ A )

= arccos —

v A 2 >

При выше заданных исходных дан-

ных критическое значение угла наклона опорной поверхности лопасти ВД составило: a = 54 ° 28' .

1 кр

Введем безразмерный параметр f N - коэффициент влияния угла a₃ на

нагрузку на лопасть ВД:

N

N   FВД f ВД  F N

^F 0ВД

A 2 - A 3

A ₂ • cosaj - A3 ’

где F N , = A_Y /( A - A3 ) - значение нор

мальной силы на лопасти ВД при a, = 0.

На рис. 3 представлен график зависимости f N от a₃. Из графика видно, что значительное влияние угла a₃ проявляется при a, >  30 ° , а при значениях угла a₃ до 15° рост нагрузки не превышает 10%.

Предcтавленная модель позволяет получить исходные данные для моделирования НДС приконтурного и элементов геохода, взаимодействующих с породой приконтурного массива.

Библиографический список 1. Бегляков В.Ю., Аксенов В.В. Поверхность забоя при проходке горной выработки геоходом: монография // Издательство: LAP LAMBERT Academic Publishing GmbH & Co. KG Heinrich-Böcking-Str. 6-8, 66121 Saarbrucken, Germany. 2012. - 139 с.

• 2.    Sadovets V.Yu., Beglyakov V.Yu. and Efremenkov A.B. 2015 Simulation of geokhod movement with blade actuator Applied Mechanics and Materials 770. 384-390.

• 3.    Aksenov V. V., Beglyakov V.Y., Kazantsev A.A., Doroshenko I.V. Development of Requirements for a Basic Standardized Mathematical Model of Geokhod // IOP Conference Series: Materials Science and Engineering. – IOP Publishing, 2016. – Т. 127. – №. 1. – С. 012031.

• 4.    Aksenov V. V., Beglyakov V.Y., Kazantsev A.A., Saprykin A.S. Substantiating Ways of

• 5.    Broere W., Faassen T.F., Arends G., van Tol A.F. Modelling the boring of curves in (very) soft soils during microtunnelling. Tunnelling and Underground Space Technology, 2007, 22 (5-6), pp. 600-609. DOI: 10.1016/j.tust.2007.06.002.

• 6.    Deng K., Li Y., Yin Z. Thrust distribution characteristics of thrust systems of shield machines based on spatial force ellipse model in mixed ground. Journal of Mechanical Science and Technology, 2016, 30 (1), pp. 279-286. DOI: 10.1007/s12206-015-1231-6.

• 7.    Deng K., Zhang X., Yang J., Wang H. Deformation characteristics under variable stiffness for the propelling mechanism of EPB shield machines in mixed ground. Journal of Mechanical Science and Technology, 2014, 28 (9), pp. 36793685. DOI: 10.1007/s12206-014-0829-4.

• 8.    Festa D., Broere W., Bosch J.W. An investigation into the forces acting on a TBM during driving - Mining the TBM logged data. Tunnelling and Underground Space Technology, 2012, 32, pp. 143-157. DOI: 10.1016/j.tust.2012.06.006.

• 9.    Huayong Y., Hu S., Guofang G., Guoliang H. Electro-hydraulic proportional control of thrust system for shield tunneling machine. Automation in Construction, 2009, 18 (7), pp. 950-956. DOI: 10.1016/j.autcon.2009.04.005.

• 10.    Kongshu D., Xiaoqiang T., Liping W., Xu C.Force transmission characteristics for the non-equidistant arrangement thrust systems of shield tunneling machines. Automation in Construction, 2011, 20 (5), pp. 588-595. DOI: 10.1016/j.autcon.2010.11.025.

• 11.    Peck R.B. Deep excavations and tunneling in soft ground. Proceedings of the 7th Int. Conf. on Soil Mechanics and Foundation Engineering, 1969, pp. 225-290.

• 12.    Shangguan Z., Li S., Luan M. Determining optimal thrust force of EPB shield machine by analytical solution. Electronic Journal of Geotechnical Engineering, 2009, 14 H.

• 13.    Sugimoto M., Sramoon A., Konishi S., Sato Y. Simulation of shield tunneling behavior along a curved alignment in a multilayered ground. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133 (6), pp. 684-694. DOI: 10.1061/(ASCE)1090-0241(2007)133:6(684).

• 14.    Vu M.N., Broere W., Bosch J. Effects of cover depth on ground movements induced by shallow tunnelling. Tunnelling and Underground Space Technology, 2015, 50, pp. 499-506. DOI: 10.1016/j.tust.2015.09.006.

• 15.    Wang L., Gong G., Shi H., Yang H. Modeling and analysis of thrust force for EPB shield tunneling machine. Automation in Construction, 2012, 27, pp. 138-146. DOI: 10.1016/j.autcon.2012.02.004.

  “Gornye nauk	i i tehnologii”/ “Mining science and technology”, 2017, No. 4, pp. 23-28
  Title:	DETERMINING THE FORCES OF INTERACTION OF MAIN GEOKHODS SYSTEMS WITH GEO-ENVIRONMENT AND WITH EACH OTHER
  Author 1:	Name & Surname: Vyacheslav Yu. Beglyakov Company: National Research Tomsk Polytechnic University, Yurga Institute of Technology, Yurga Address: 652050, Yurga, Leningradskaya str., 26 Scientific Degree: Dr. Sci. (Tech.) Work Position : associate professor Contacts: begljakov@rambler.ru
  Author 2:	Name & Surname: Aksenov Vladimir V. Company: Institute of Coal of the Siberian Branch of the RAS Address : 650000, Kemerovo, ave. Sovetski, 18 Scientific Degree : Dr. Sci. (Tech.) Work Position : Professor
  Author 3:	Name & Surname : Irina K. Kostinets Company : Branch of Kuzbass State Technical University named after T.F. Gorbachev in the town of Belovo

  Address: 652644, Kemerovo Region, Belovo, town of. Inskoy, st. Ilyich, 32a Work Position : principal

МИСиС

Load Application When Modeling Interaction of a Multiincisal Mining Machine Actuator With Rocks // IOP Conference Series: Materials Science and Engineering. - IOP Publishing, 2016. -Т. 127. - №. 1. - С. 012032.

Author 4:

Name & Surname : Aleksey A. Khoreshok

Company: T.F. Gorbachev Kuzbass State Technical University

Address: 650000, Kemerovo, Vesennyaya Str., 28

Scientific Degree : Dr. Sci. (Tech.)

Work Position : Professor

DOI:

10.17073/2500-0632-2017-4-23-28

The processes occurring during the geodetic excavation of underground excavations are characterized by the interaction of the elements of the geokhod with each other and with the geo-environment. The interaction process can be investigated in mathematical modeling, solving the problems of justifying the parameters of the drives and interacting forces, ensuring sufficient strength of the machine elements and the bearing capacity of the contour array. The proposed block-modular principles of constructing a mathematical model allow solving particular problems of the system and its individual elements. From the solution of particular problems, it is now necessary to proceed to the solution of the generalized model, using equivalent loads and reduced total moments (forces). The construction of a generalized model requires a number of assumptions, but its solution will reveal the interaction between the elements of the geokhod and the geo-environment, which is very relevant.

As an example, the solution of a particular problem is given-the determination of the value of the forces arising from the interaction of the blade of an external engine with the medium.

A list of assumptions is formulated that allow us to describe a general mathematical model of the interaction between the geo-environment and the geokhod, as well as the processes occurring during geodetic excavation of mine workings.