Определение синергетической эффективности грузоперевозок

Важность логистических систем неуклонно возрастает на современном этапе развития экономики, международных торговых и транспортных коридоров. Эти системы объединяют поставщиков продуктов, производителей, транспортных компаний и потребителей.

Анализ источников литературы по логистическим системам позволяет выделить по крайней мере два разных подхода к их исследованиям [1]. В первом подходе вся логистическая система рассматривается как система, которая стремится достичь максимальной совокупной эффективности.

В этом случае местные критерии участников подчиняются глобальным критериям. Основным критерием эффективности является минимальный совокупный расход и минимальное время доставки продукта.

Следует отметить, что при таком подходе конкуренция между участниками в открытом виде не учитывается. Однако, даже если все участники работают вместе для одной цели, тогда между ними в любом случае существует конкуренция - даже если они находятся на этапе обмена результатами по достижению цели.

Во втором подходе логистическая система рассматривается как система, в которой участники независимы и следуют своим собственным интересам. В этом случае исследуются равновесное и оптимальное состояние участников по различным критериям эффективности [2].

На наш взгляд, второй подход может считаться более адекватным рыночной среде. Действительно, ни одна логистическая система не может эффективно работать без взаимного согласия экономических интересов ее участников.

Здесь к месту было бы привести цитату из книги Л.М.Миротина. Л.Миротин пишет: «Мы и раньше, то есть в период социализма, серьезно занимались оптимизацией производства, транспортировки, снабжения, продаж, торговли и других сфер. Но государственная монополия вызывала гигантские противоречия среди участников всей системы товарных потоков. Результат же чаще всего был таким: огромные потери по всей цепочке движения товаров, чрезмерные издержки и, следовательно, повышение цен на продукты» [3].

Таким образом, именно экономические интересы участников являются первостепенным вопросом при экономико-математическом моделировании логистических систем в рыночной среде.

Если учитывается конкуренция между участниками логистической системы и поведение потребителей (даны цены, тарифы и объемы), и если все подчинено общей цели (например, общая совокупная прибыль, минимальные затраты), то это становится скорее технологической задачей, чем экономической.

Поскольку взаимные экономические воздействия рыночных агентов трансформируются в технологические воздействия: интенсивность погрузки-разгрузки, управление скоростью транспортных средств и т.д.

Критерием оптимизации деятельности участников логистической системы должны выступать не затраты, а доход. Однако критерий минимальных затрат имеет смысл лишь тогда, когда с самого начала известно, что будущие доходы превысят сегодняшние затраты.

Очевидно, что в данном случае такое условие не может быть принято в обязательном порядке при моделировании деятельности предприятий автотранспорта в рыночной среде. Расходы сами по себе не являются важными, расходы являются важным показателем в отношении к полученным доходам. Оптимальное планирование ограниченных ресурсов возможно в логистической системе именно из-за критерия доходности.

Следует отметить, что условие создания интегрированной логистической системы является потенциальной возможностью получения синергетической эффективности. В качестве синергетической эффективности можно продемонстрировать увеличение доходов участников логистической системы в результате интеграции [4].

Таким образом, большая важность заключается в нахождении баланса между участниками в модели логистической системы и определении синергетической эффективности, создаваемой объединением участников интегрированной системы логистики.

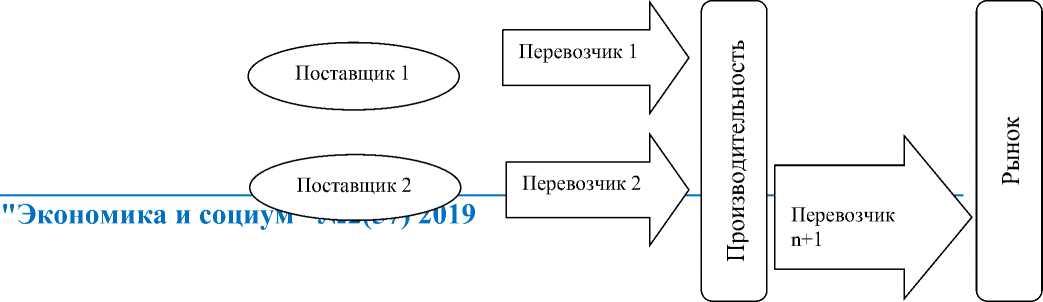
Для проведения анализа исследуем модель логистической системы, структурно идентичную модели в [4] (рис. 1).

• • •

Поставщик n

Перевозчик n

Рисунок 1. Логистическая система.

Представленная логистическая система состоит из:

• •    S i - n частных поставщиков ресурсов с добавленной стоимостью, i е N , N = { 1,2,..., n } ;

• •    z i - единица i -го ресурса, перевозимая n -м транспортным средством; i е N ;

• •    V ¹ - частный производитель товара с добавленной стоимостью;

• •   Z_{n +1}-транспортное  предприятие, перевозящее единицу продукта с

добавленной стоимостью (индекс n+1 );

• • потребительский рынок, здесь цена формируется как P = b - k • Q ;

здесь b >0 потенциал рынка (максимально возможная рыночная цена продукта);

k ^ 0 - показатель гибкости спроса (снижение цены потребительского рынка при индивидуальном росте объема производства);

Q >  0 - объем производства и поставки продукции на рынок.

Таким образом, производитель в технологическом процессе выпускает продукт с использованием n видов ресурсов. Особенность технологического процесса заключается в том, что количество необходимых ресурсов пропорционально объему выпускаемого товара. В этом случае ресурсы не являются взаимоисключающими. В этих условиях производственная функция изготовителя может быть выражена следующим системным уравнением:

Ri = acQ, i е N,

здесь R - объем i-го ресурса, необходимый для производства Q объема;

d i - технологический коэффициент, является нормой распределения ресурсов на единицу готовой продукции.

Каждый ресурс покупается производителем у отдельного поставщика на условиях EXW (Ex Works – со склада производителя). В таких обстоятельствах производитель сам оплачивает поставку ресурсов поставщикам.

Для доставки ресурсов производитель использует услуги n независимых транспортных предприятий. Готовая продукция также доставляется на потребительский рынок n + 1 независимыми транспортными предприятиями.

В этом случае параметры логистической системы должны отвечать следующим ограничительным условиям:

А — b — v — гп+1

^-^^d i ^ S i ieN

^d i • z i > 0 ieN

здесь A - экономический потенциал логистической системы.

Положительным значением экономического потенциала является необходимым условием создания и функционирования логистической системы.

Каждый член логистической системы пытается максимизировать свою прибыль. Давайте рассмотрим экономический интерес каждого участника с реакцией на оптимистичное поведение его конкурентов.

F^ist = Q ⋅ ( b - k ⋅ Q - v - p_{n + 1} - ∑ a_i ⋅ d_i - ∑ a_i ⋅ p_i ) → max (1)

i ∈ N           i ∈ N                 ^Q

Мы принимаем первую производную от дохода производителя равным нулю:

_dF ist dQ

= 0

= b - 2 ⋅ k ⋅ Q - v - p_{n + 1} - ∑ a_i ⋅ d_i - ∑ a_i ⋅ p_i i ∈ N            i ∈ N

Отсюда можно найти функцию оптимальной реакции производителя при данных ценах на ресурсы и транспортных тарифах:

b - v - P n + 1

Q =-------

- E a i • d i - E a i • р^ i e N            i e N

2 • k

Вторая производная

d ² F is

---— = -2 • k ^ 0, т.е. максимальный доход dQ2              , производителя достигается именно при этом объеме производства.

Поставщики ресурсов максимизируют свои доходы по своим ценам и ценам других поставщиков и тарифам для транспортных компаний. Целевая функция i- го поставщика ресурсов представляется следующим образом:

F^ ab = R_t • ( d - _Si ) = a • Q • ( d - _Si ) ^ max i e N            (3).

di

Подставляем (2) в (3) и получаем:

^Fi^sab = vV • ⁽ b ^- v ^- P n + i ^- E a i ■ ^d i ^- E a ^- р^ ) • ⁽ d i ^- s i ) ^ max i ^{e N 2} • ^k                        i e N            i e N                                d i

Найдем первые производные и приравняем их к нулю:

sa b dF dd

ai к

--b — v — p

2 • k

\

n + 1

^{- 2} • ai • ^di ^- E a i ^ ^di - E

j e N / i

^

^ai • Pi ⁺ a i • s i )   = ⁰, i ^{e N}

i e N

отсюда находится оптимальное значение i- го ресурса:

b-v-pn+i- E aj • dj -Eai'Pi+ ai's j e N / i               i e N

этой цене мы

• d. =-------------- j -----------------------------, i e N

• i                                 2 • a_;

j 2 r^ ted dFa

Вторая производная ----—= - ^ 0, i e N, то есть при dd2k получаем максимальную прибыль поставщика i-го ресурса. Подставив полученные n выражений (4) друг в друга и произведя преобразования, находим внутренние равновесные цены ресурсов согласно Курно:

b - v - р - 2 • a_f • d_f - V a_f • d, -V a. • p , + a,. • s ,) = 0

n+1               i       i                i       i                i       i         i i i e N          i e N b- v- Pn+i-E ai- si-E ai- Pt d = s, +-------------ieN--------ieN------, i e N.

i i                    a • ( n + 1)

Поставляющие ресурсы транспортные предприятия максимизируют свои доходы при своих тарифах и в рамках данных тарифов и цен на ресурсы других транспортных предприятий. Целевая функция i-й транспортной организации может быть выражена следующим образом:

FT = Ri •(Pi -zi) = ai • Q• (pi — zi) ^ max,i e N(6)

pi

Подставляем (2) в (6):

^F i^T = arr • ⁽ b ^- v ^{- p} n + ^{1 -} 2 a i- d i — 2 a • p> ) • ⁽ Pt ^- zJ ^ ^max i ^g N

• 2    • k                     ieN           ieN

Находим первые производные и приравниваем их к нулю:

dF_i ^T     a_i

=w ^{( b -} v ^{- p}n + i ^{- 2} • ^ai • pt dp_t 2 • k

- 2 a • pt- 2 ai • di+ a • z)=0, ie N i∈N

j e N / i

Отсюда находится оптимальная цена i-го транспортного предприятия:

b ^- v ^- P n + 1

^pi ⁼

Вторые производные

• - a ⋅p - a ⋅d +a ⋅z i        i                 iu        i          ii

j e N / ii

• —-------------------------, i e N .

• 2 • a_t

2 T2

dFa

• —i— = —i- ^ 0, i e N, то есть получаем максимум dp г

функции дохода i-го транспортного предприятия при таком тарифе.

Подставляя n выражений в полученные выражения (7) и произведя преобразования находим сбалансированные транспортные тарифы по Курно:

b - v - P n + i - 2 a • ^zi - 2 a i- ^di

p * = z_t +------------ ^N -------^----, i G N .

i i                     a_t • ( n + 1)

Поставляющие продукцию транспортное предприятие максимизирует свой доход при своих тарифах и в рамках данных тарифов и цен на ресурсы других транспортных предприятий. (n +1) является целью Целевая функция (n+1)- го транспортного предприятия выглядит следующим образом:

F T+1 = Q • ⁽ p n + 1 ^{- z}n + 1 ) ^ max, (9)

Подставляем (2) в (9) и находим:

с т ^г п+1

т^ -(b-v- p_n +i - ^ard i -^afP i Y (P n+i \                  ieN           ieN       /

-^ n+1 ) ⁴ ^ax,

Находим первую производную и приравниваем ее к нулю:

T

^+1 = Tk(b-V-2' Pn+1 - ^N ai'Pi — E+n afdi+ Zn+1) = 0

Из (10) находится оптимальный тариф (n+1)- го транспортного предприятия.

d2FT1

Вторая производная    —-— = —  < 0 , то есть при таком тарифе dp2+1       к обеспечивается максимум доходной функции (n+1)-го транспортного предприятия.

Чтобы найти баланс Курно между поставщиками ресурсов и транспортными предприятиями, объединяем выражения (5), (8) и (10) в систему.

В результате получаем 2n+1 уравнений (11):

b - v - Pn+1 -Е ai • s -Е a • Pi i e N           i e N

d i = s i +

, i e N

a • ( n + 1)

Pt =+⁺

b - v - P n + 1 - Е a i- zi — Е a i • d i

i e N           i e N

a • ( n + 1)

, i e N

b - v - zn+1 -Е a+ р^ -Е ai- di i NieN pn +1 zn +1 +                   ~                   , i e N

Решив систему уравнений (11), находим:

- равновесные значения ресурсов:

d e = s i +

A

2 • a_t • ( n + 1)

i e N ,

- равновесные тарифы транспортных предприятий, перевозящих ресурсы:

e

Pi = ^z i ⁺

A

2 • a_t • ( n + 1)

i e N

- равновесные тарифы транспортных предприятий, доставляющих продукцию на рынок:

e A

.

^Pn + 1    z n + 1 ⁺     z     IX

2 • ( n + 1)

Подставляя (9), (10) и (11) в (12), находим равновесный объем продукции:

A

_Qe ₌

4 ⋅ k ⋅ ( n + 1)

•

Тогда равновесные доходы поставщиков ресурсов выражаются так:

Fsab =      A     ,i ∈ N i       8⋅k⋅(n+1)2

•

Равновесные доходы транспортных предприятияй, доставляющих ресурсы:

т А

FT =     A     ,i∈N i 8⋅k⋅(n+1)2

Равновесные доходы

транспортных предприятияй, доставляющих

продукцию на рынок:

FiT

A ²

8 ⋅ k ⋅ ( n + 1)^2,

Равновесный доход производителя продукции:

_F ist ₌       ^A

16 ⋅ k ⋅ ( n + 1)²

•

Общий равновесный доход логистической системы:

i ∈ N

Fsab +   FT +FT +Fist i                   i          n+1

i е N

A ² ⋅ (4 ⋅ n + 3)

16 ■ к • ( n = 1)² •

Предположим, что все участники для достижения синергетического эффекта объединены в интегрированную логистическую систему. В этом случае у них возникает единая функция дохода:

F = Q ■ ⁽ b - k ■ Q - v - z n + i ^- ^ a ■ s i - 2 a ■ z ) ^ max (15) i ∈ N i ∈ N ^Q

Первую производную функции (15) приравниваем к нулю:

= Ь - 2 • k ■ Q - V -zn+i-2 ai • si -2 ai ’ zi = 0 • dQ                          i∈N       i∈N

Отсюда находим оптимальный объем производства и поставки продукции:

Q ∗ = ^A

2 ⋅ k

Доход интегрированной логистической системы выражается следующим

образом:

4 • k

Сравним общий доход участников до и после интеграции:

A² _ A ² • (4 • n + 3) _ A ²    ( 2 • n + 1 ^ ²   ₀

4 • k 16 • k • ( n + 1)² = 16 • k \ n + 1 )

Таким образом, в этом выражении количественный показатель S характеризует синергетический эффект, полученный участниками логистической системы в результате интеграции. В условиях баланса Курно поставщики ресурсов и транспортные предприятия являются монополистами по отношению к производителю и получают монопольную прибыль.

При объединении поставщики и перевозчики отказываются от монопольных цен и тарифов из-за общего дела. В результате они зарабатывают больше за счет увеличения объемов перевозок. В этом и заключается синергетика логистической системы при интеграции участников.

Однако следует разработать механизм распределения полученных доходов для протекания процесса интеграции. А это требует нахождения оптимальных транспортных цен и тарифов. Эта чисто экономическая задача является предметом будущих исследований.