Определение скорости движения частиц твердых органических удобрений по поверхности ротора сферического типа

Сферические рабочие органы почвообрабатывающих машин имеют очень широкое применение. Однако на машинах для поверхностного внесения твердых органических удобрений (ТОУ) такие рабочие органы не использовались. Поэтому авторами настоящей статьи была разработана конструкция сферического ротора для разбрасывателя ТОУ. Такой рабочий орган имеет горизонтальную ось вращения и выполнен в виде сферы, в которой лопасти имеют форму секторов, боковые кромки которых проходят по эвольвентной кривой. При этом величина сектора лопасти равна величине сектора промежутка.

Работает ротор следующим образом. Частицы удобрений, захватываемые сферическим ротором, совершают сложное движение: переносное вращательное вместе с ротором и относительное по его рабочей поверхности. В результате частица, поступающая на поверхность ротора в точке М 0 , начинает двигаться по траекториям S а в абсолютном и S r в относительном движениях (рис. 1), через некоторое время окажется в точке М .

Рис. 1. Схема движения частиц удобрений по рабочей поверхности сферического ротора

Абсолютная скорость частиц на поверхности диска представляет собой геометрическую сумму переносной υ е и относительной υ r скоростей:

^υ а ⁼ ліυ _е ² + υ _r ² + 2 υ _е υ _r cos δ , (1) где δ – угол между направлением скоростей υ е и υ r , град.

Переносную скорость определяют угловой скоростью ротора ω и местом распо- ложения частиц на его поверхности:

υ _е = ω r ,            (2)

где r – радиус от оси вращения ротора до рассматриваемой частицы, м.

Угловую скорость ротора определим по формуле [1]

_{ω =} υ П cos β _{,            (3)}

RР где   υП – поступательная скорость рото ра, м/с;

Положение частиц относительно оси вращения ротора r = Rsinϕ,               (4)

где R – радиус сферы диска, м;

φ – угол, определяющий положение частиц относительно оси вращения ротора, град.

С учетом (3) и (4) выражение (2) примет вид:

υ _е

υ R cos β sin ϕ R Р

Чтобы определить υr, необходимо составить и решить дифференциальные урав- нения относительного движения частиц по ротору.

Частица удобрений М (рис. 2), находящаяся на поверхности диска, может совершать относительное движение по дуге ОА с радиусом сферы R и по дуге окружности радиусом r .

β – угол атаки ротора, град.;

R Р – радиус ротора, м.

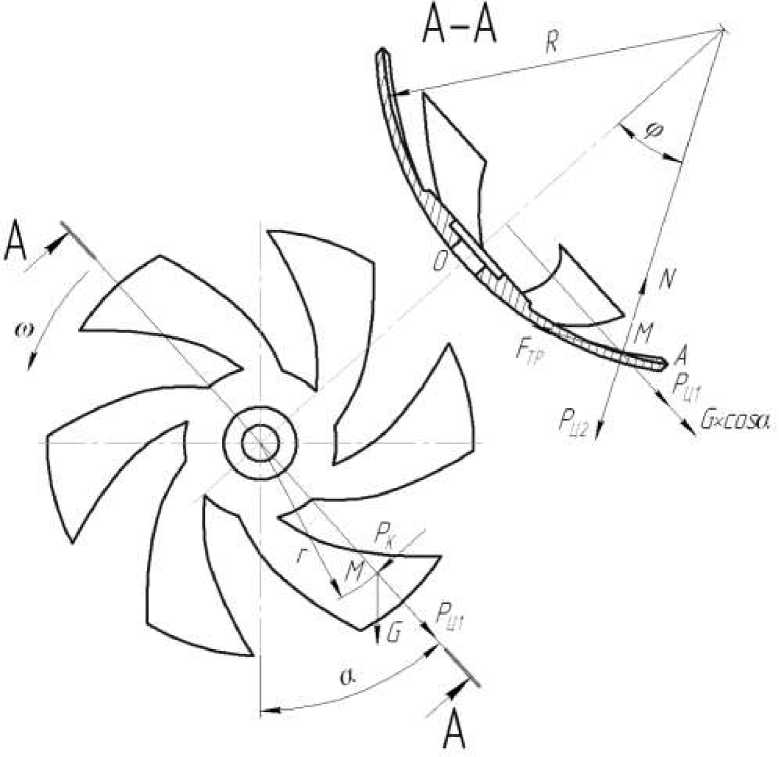
Рис. 2. Схема сил, действующих на частицу удобрений при взаимодействии со сферическим ротором

Однако в связи с тем, что частицы, находящиеся на поверхности ротора, постоянно подпираются валком удобрений, которые непрерывно поступают на ротор в ходе поступательного и вращательного движений, можно считать, что в относительном движении они перемещаются только по дуге ОА .

Рассмотрим этот случай в динамике. На частицу удобрений М действуют: сила тяжести G, центробежная сила инерции от вращательного движения ротора РЦ1, центробежная сила инерции, вызванная относительным движением частицы по дуге сферы ротора РЦ2, нормальная сила, приложенная к частице со стороны рабочей поверхности ротора N, сила трения FТР, сила Кориолиса РК, возникающая в результате вращательного движения ротора и отно- сительного движения частицы по дуге рабочей поверхности.

где

Сила тяжести

G = mg, m – масса частицы удобрений, кг;

g – ускорение свободного падения, g=9,81 м/с2.

Центробежная сила инерции при вращении ротора

Рц j = m to ² R sin ф .

Центробежная сила инерции относительного движения p =

¹ Ц 2

m U 2

R

.

Нормальная сила, приложенная к частице со стороны рабочей поверхности ротора,

mu

N = r + mg sin фcos a + mto R sin ф, где α – угол поворота диска, град.

Сила трения

X

Fj, = fm ^r- + g sin ф cos a + to ² R sin ² ф , ТР       V R

где f – коэффициент трения почвы о материал ротора.

Сила Кориолиса

С учетом сделанных допущений и действующих сил дифференциальное уравнение относительного движения частицы удобрений по дуге ОА рабочей поверхности ротора имеет вид

.

.

to ² R sin2 ф j .          .   2„ • 2  \ z^

----~—~ - f ( g s^m Ф cos ^a + to R ^sin ф ) • (6)

R dr + fRФ = gcosФcosa + dt

.

V 7

Уравнение (6) с учетом начальных условий ( φ = φ 0 и φ =0) имеет вид

.

ф = - е ^{2 f ( ф} 0^{- ф} )

Л л г \ 4 ffe

V(1 + 2 f)R J

z

cos ф ₀ cos a + ^ g 1

—

V V

1 + 2 f

Г to 2 1

+ — sin 2 ф о

V f 7

—

r   4 fg

+ 2 g 1

—

R

V

4f_

V(1 + 2 f)RJ

cos ф cos a +

to sin ф + — Sin2ф

V J 7

- to ² sin ф •

С учетом u ² = ф R ² найдем зависимость для определения относительной скорости перемещения частиц по рабочей поверхности сферического ротора:

и

—I

2 f ( ф ₀ —ф ) е

+

/ А Г Л 4^ 6^

V ( 1 + 2. f ) R ^J

cos ф cos a + 2 gR 1 V

—

Г ^f

V 1 + 2 f

Г ro ² R ² J

V f J

Г 4 fgR

A

V ¹ + ² f J

cos ф cos a +

+ 2 gR 1

V

Г ^ f ² JJ

V 1 + ² f J J

sin 2 ф — ro ² R ² sin ф .

Подставив в выражение (7) значение ω , окончательно получим

^U 2

,^{2 f} ( ф о ^— ф ) ^{Г 4} fg ^R

V 1 + 2. f J

Г cos ф cos a + 2gR 1

V

—

V 1 + 2 f J J

П ²

Г R

V ^RP J

J2     , cos в

^{Г si}n² Ф о

—

V

f

sin ² ф о J

+

Г g J

V 1 + 2 f J

cos ф cos a +

Г

+ 2 gR 1

V

-

Г f_ V 1 + 2 f

sin ф + U ²_n

Г R

V RP J

V .

^{cos в}

г sin2 ф V f

-

J ^sin ф .

J

Подставив в выражение (1) значения υ е из (5) и υ r из (8), а также с учетом того, что при перемещении частиц в относи-

тельном движении только по дуге с радиусом сферы ротора R угол δ =90°, получим

/

U = 1

^U n

V

Г

+ 2 gR 1

V

-

V

R J

— cos в sin ф

^RP J

Г ^f

V 1 + 2 f

J

sin Ф _о + U_n

( R

,2 f ( ф о — ф ) ^{Г 4 fgR}

cos ф cos a +

V RP J

^cos 2 ^в

^{r s}Іⁿ² Ф о V f

-

sin ² ф о J

+

+

Г f J V 1 + 2 f J

Г cos фcos a + 2 gR 1

V

-

(I4 f y JJ

V ^{1 + 2} f J J

² sin ф + U _n

V R P J

cos ² в

-

■ ² J sin ф ГГ

J

. (9)

Заменив в (16) ф на arcsin( R_P/R ), sin ф на ( R_P/R ) и cos ф на RR ² — R 2 / R , найдем абсо-

лютную скорость частиц в момент схода с ротора:

Ua = {('

M 2 .

v_n cos в ) +1 — е

R

^{2 f} ( ф о - arcsm— R

) Г^{Г 4} fg ^R )

LV ¹ + ² f J

cos ф cos a +

Г

+ 2 gR 1

V

—

Г ^f

V 1 + 2 f

sin ф ₀ + и

V R P J

cos

² в

Г sinM

— sin

J ф о

J

+

+

^{Г 4} fg^R ² — R P ^J

V 1 + 2 f

J

Г cos a + 2 gR 1

V

—

Г ^f

V 1 + 2 f

⁺ U n

Г R

V R P J

cos ² в

Следовательно, υ а зависит

2 R _Р R ²

—

^RР ²

Г R

A 2 J

V

fR ²

—

V ^RP J J

.

от кон-

структивных параметров ( R , R Р ) и их соот-

ношения, а также от режимов работы ( υ П , f , углы φ , α , β ).

Полученные зависимости позволяют определить скорости частиц твердых органических удобрений, находящихся в любой точке рабочей поверхности сферического ротора, и могут быть использованы при обосновании параметров и схемы расположения рабочих органов разбрасывателей удобрений.