Определение скорости космического аппарата в негеостационарных системах персональной спутниковой связи

В общем случае точность определения положения и скорости объекта в пространстве зависит от комбинации типов используемых измерителей, ошибок измерений и расположения средств измерений относительно объекта [1–4]. Так, известно, что наибольшая точность метода определения вектора скорости в пространстве, основанного на непосредственном способе измерениях трех радиальных скоростей объекта, достигается при таком взаимном расположении трех измерительных станций, при котором расстояния a (базы) между

станциями равны, то есть образуют равносторонний треугольник с отношением базы к высоте пирамиды равным [5]:

h / a = ¹ = 0, 408.

6,

Используя данное отношение применительно к существующим космическим системам, использующим разные типы орбит, можно оценить расстояние между измерителями, обеспечивающее наибольшую точность метода (табл. 1).

Из табл. 1 следует, что только для спутниковых систем на низкой круговой орбите возможна конфигурация с оптимальным расположением измерителей в пределах размеров земной поверхности. Данный тип орбит широко используется современными системами персональной спутниковой связи (Iridium, Globalstar), основу которых составляют КА с многолучевой антенной системой на базе активных фазированных решеток. Такие антенные системы позволяют организовать на земной поверхности зону обслуживания диаметром 4600–5800 км, образованную независимыми лучами, число которых в случае системы Iridium достигает 48. При этом эквивалентная ширина диаграммы направленности (ДН) каждого луча

Таблица 1

Оптимальные расстояния между измерителями для различных спутниковых систем

Орбита Орбитальная группировка Высота h орбиты, км Расстояние между измерителями, км LEO Iridium, Gonets, Globalstar 780...1500 1912...3674 MEO GPS, ГЛОНАСС 18840...20180 46176...49460 HEO Молния, Tundra 40000...47000 98039...115126 составляет ±11...12°, а формируемая им зона обслуживания составляет около 650 км [5; 6].

Учитывая эти особенности, представляется возможным определять скорость движения космического аппарата бортовыми средствами в реальном масштабе времени путем проведения одновременных измерений доплеровских сдвигов частот сигналов в разнесенных абонентских каналах.

Из теории и практики применения многолучевых доплеровских измерителей вектора скорости известно, что при горизонтальном полете возможно определение вектора скорости летатель- ного аппарата с проведением измерения частоты Доплера по двум лучам [6]. Данный способ можно считать приемлемым для задачи измерения вектора скорости КА, пренебрегая крайне незначительными изменениями его вертикальной составляющей (рис. 1).

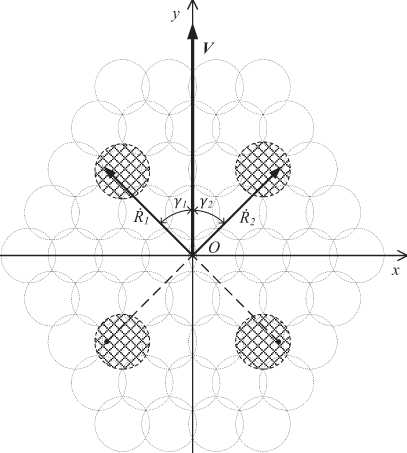
Рис. 1. Направления измерения доплеровских частот сигнала для КА с многолучевой антенной

Для V -расположения лучей, характеризующимся равенством углов γ ₁ = γ ₂, составляющие V_x , V_y определяются следующим образом:

у _ А0 , fd 1 + fd 2 у = - Л , fd 1 - fd 2

x 4 cos y y 4 sin y где λ0 – длина волны излучаемого сигнала; fd1, fd2 – измеренные доплеровские частоты; γ1, γ2 – углы направления измерений.

Проведем потенциальную оценку точности определения скорости движения КА предлагаемым способом с учетом влияния возможных ошибок.

Учет возможных ошибок определения вектора скорости

При оценке точности определения вектора скорости в пространстве необходимо найти связь между составляющими вектора ошибки δ V и тремя компонентами вектора скорости объекта V , измеряемыми радиотехническими методами [7; 8].

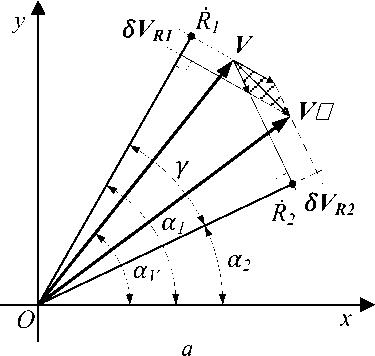
Применительно к задаче определения скорости космического аппарата будем считать, что его перемещение осуществляется только в горизонтальном направлении ( V_z = 0) и задача сводится к поиску значения и направления вектора скорости V на плоскости. Так, расчетное значение вектора скорости будет определяться точкой пересечения прямых, перпендикулярных двум радиальным составляющим R ₁ и R ₂ (рис. 1). Направления вектора скорости V и радиальные направления задаются относительно одной из координатных осей углами α_V и α_{R 1}, α_{R 2}. При этом имеющиеся ошибки измерения радиальных скоростей δ R ₁ и δ R ₂ ведут к возникновению погрешности полученного значения вектора скорости, который определяется отрезком OV ʹ (рис. 2a).

-

Том 2

Рассмотрев параллелограмм ошибок вектора скорости VAV ʹ B, можно найти проекции вектора ошибки VV ʹ на координатные оси δV_x и δV_y , которые составляют:

5V x	5Vm   ( =     R 1 cos 1 Sin Y    ^	n 1   3VR2    ( « 2        1       R 2 cos 1 2 ) sin y	n a + 1 2
5 V y	5VRv ■  ( =     R 1 sin 1 Sin Y	2    n )   8V « 2   J+ ■ R 2 sin 1 v     2 )  Sin Y	П a +— 1 2

,

Таким образом, линейная ошибка в направлении соответствующей стороны параллелограмма ошибок увеличивается в 1/sin γ раз. С учетом этого фактора выражения (1) для ошибок в направлении осей X и Y примут вид:

3VR,+ VЗа   (

3VX = —-—-—1 cos I а sin у       V

п

—

.

Кроме этих ошибок, обусловленных неточным измерением величин радиальных составля- ²⁰⁰ ющих, на результирующую точность определения вектора скорости также оказывают влияние ошибки, обусловленные неточным определением направления на объект (рис. 2б). При этом ошибки определения угла приводят к отклонению линии направления V_R на угол δα и возникновению линейной ошибки, которая составляет:

V ∙sin( α_V – α ) δα = V_t δα , где V_t – тангенциальная составляющая вектора скорости.

3V, + V За   (   п

—R2—t—- cos I а + -sin y       V     -

8Vy =

sin y

8V„ 2 + V 8a

R 2 t 2

sin y

■  (    . n)

sin a +

( 1   2)

к

+

Оценка точности определения скорости КА

Проведем оценку влияния ошибок измерения радиальных скоростей в двух, выбранных

симметрично относительно вектора движения КА, направлениях (рис. 3).

С учетом симметричности выражения (2)

принимают вид:

5V x

3VR + V sin( a - a^)3a sin y

• cos I a

^{3 V}y

П)    /   . П)

- cos a +

2)       I 1   2 J.

3VR + V sin(a7 - a^)3a sin y

sin I a

П Y ■ <   . П)

— + sin a +—

2)      I 1   2)

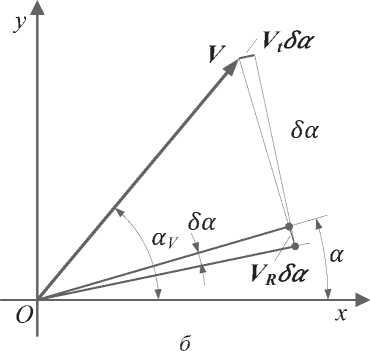
Рис. 2. Ошибки при измерении радиальной составляющей ( a ) и определении направления на объект ( б )

Результаты оценки точности измерения радиальных составляющих, в зависимости от угла γ между направлениями, представлены на рис. 4. При расчетах погрешность измерения радиальных составляющих, обусловленная аппаратурной погрешностью и средой распространения сигнала, принималась равной δV_{R 1} = δV_{R 2} = 1 %, а ошибка направления – равной ширине диаграммы направленности δα = ±10°.

Полученные графики на рис. 4 показывают, что наибольшая точность определения скорости (по обеим осям) соответствует случаю, когда радиус-векторы пересекаются под прямым углом. При этом значительную долю погрешностей вносит ошибка, обусловленная неточностью измерения направления, которая имеет тенденцию к снижению при уменьшении угла между направлением измерения и истинным направлением векто-

ра скорости КА. Относительно высокое значение погрешности обусловлено неопределенностью местоположения абонента внутри зоны обслуживания, формируемой шириной луча.

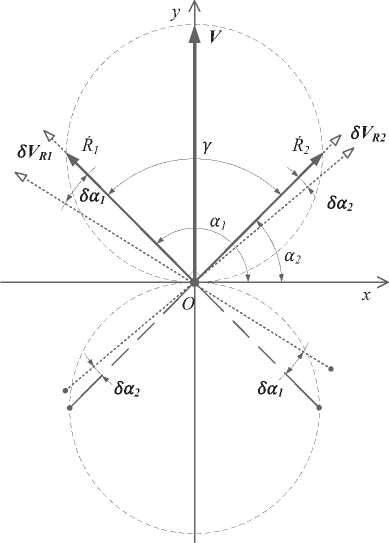
Рис. 3. Составляющие скорости движения КА с учетом возможных ошибок

На рис. 5 представлен график, отражающий вклад ошибки определения направления измерения в общую ошибку определения вектора скорости, по которому можно оценить возможность повышения точности для данного способа. Из графика следует, что для снижения результирую- щей ошибки, вызванной неточным определением направления, до уровня принятой ошибки измерения радиальной составляющей, необходимо обеспечить погрешность определения направления измерения не более 0,4°.

Снижение этой неопределенности до столь малых значений путем уменьшения ширины ДН лучей представляется нецелесообразным, поскольку такой подход потребует многократного увеличения апертуры антенной системы. Наиболее привлекательным способом выглядит использование данных о местонахождении задействованного абонентского терминала. Так, в рассматриваемых спутниковых системах предусмотрено предоставление услуг по определению местоположения абонента автономными средствами, где при однократном измерении точность определения местоположения может достигать ±1,6 км [9; 10]. Использование этой информации, переданной на борт КА по служебному каналу, позволит значительно сократить (~ в 200 раз) неопределенность направления доплеровского измерения δα внутри луча до уровня 0,12°, и получить, таким образом, ошибку направления измерения порядка 0,3 %, что не превышает принятого значения ошибки измерения радиальной составляющей.

Дальнейшее снижение погрешности определения скорости КА рассматриваемым способом возможно с использованием глобальных навигационных систем (GPS, ГЛОНАСС ), что позволит получить более точные данные о местоположении абонента и, как следствие, свести к минимуму ошибку, вызванную неточным измерением радиальной составляющей.

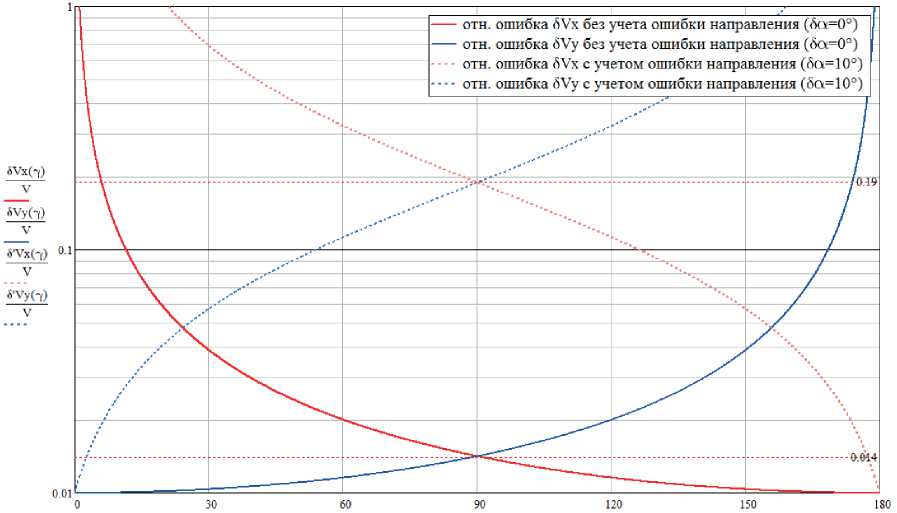
Рис. 4. Зависимость ошибок составляющих вектора скорости от угла между направлениями измерений

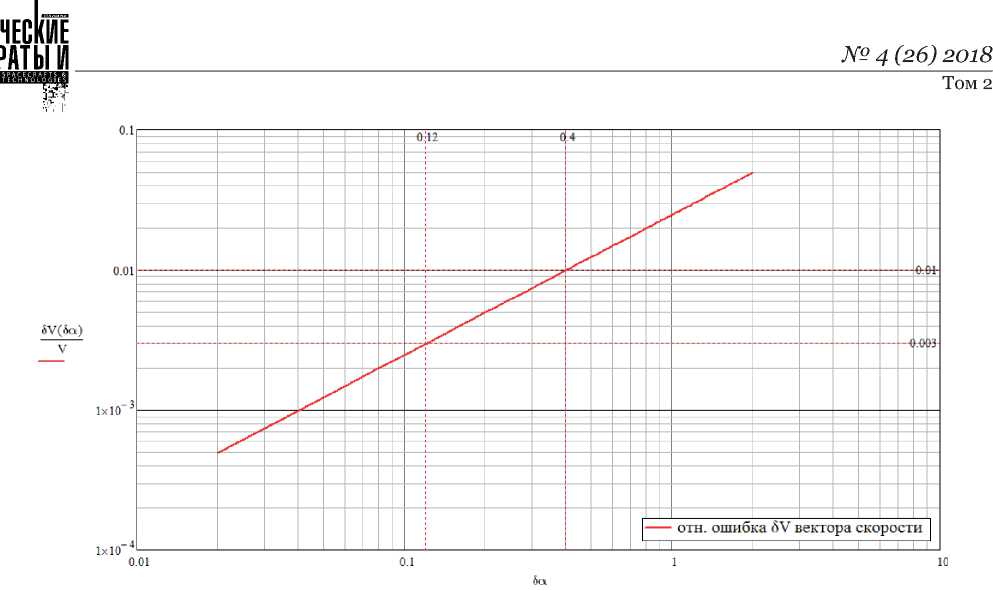
Рис. 5. Зависимость относительной ошибки вектора скорости от неопределенности направления измерения

Заключение

Проведена предварительная оценка достижимой точности определения скорости негеостационарного космического аппарата с использованием многолучевой антенной системы.

С помощью построенных зависимостей показано, что на результирующую точность определения вектора скорости КА преимущественное влияние оказывают ошибки, обусловленные неточным определением направления КА–абонент.

Получены оценки, подтверждающие, что действенной мерой для снижения погрешности, вызванной неопределенностью положения источника излучения доплеровского сигнала, может оказаться использование информации о местоположении абонента.