Определение скоростных параметров космических аппаратов по измерениям в ретрансляционных системах

В космических системах ретрансляции (КСР), наряду с передачей телеметрической, командно-программной и служебной информации, могут проводиться измерения текущих навигационных параметров (ИТНП) космических аппаратов (КА) – абонентов КСР и самих спутников – ретрансляторов. При этом может быть существенно сокращен интервал прогнозирования параметров движения КА-абонентов и соответственно уменьшены погрешности знания данных параметров на момент решения целевых задач или проведения динамических операций [1; 2].

^* Статья подготовлена при финансовой поддержке гранта Президента Российской Федерации, проект № МД-4052.2018.8 «Методы получения и обработки внеатмосферной информации для обнаружения и идентификации космических объектов в широком спектральном диапазоне».

18 в ыпуск 3/2019

Точностные показатели орбитальных определений по ретрансляционным измерениям через один спутник-ретранслятор сопоставимы с получаемыми многопунктным наземным комплексом по многовитковым измерениям непосредственно в зоне видимости КА с наземных пунктов. В случае проведения измерений через два СР, существенно разнесенных по долготе, возможен оперативный контроль динамических операций с КА-або-нентом. Таким образом, контроль параметров движения КА в КСР позволяет получить приемлемую точность без ограничений, присущих наземному измерительному комплексу. Для низкоорбитальных КА, оснащаемых навигационной аппаратурой потребителей космических навигационных систем, ретрансляционные измерения могут использоваться в резервном контуре траекторного контроля [3].

Технически обеспечение траекторного контроля КА-абонентов незначительно усложняет КСР. Ретрансляционные скоростные измерения по доплеровскому смещению несущих частот в радиолиниях вообще не сказываются на информационном обмене с КА. Вследствие относительно высокой информативности скоростных измерений низкоорбитальных КА-абонентов дальномерный режим может рассматриваться как дополнительный, проводимый в основном для уточнения положения СР [4].

Интерпретация доплеровских измерений в космических ретрансляционных системах и определение по этим измерениям скоростных параметров движения КА-абонентов имеет ряд особенностей.

Рассмотрим ретрансляционную измерительную систему (рис.), в которой наземный передающий пункт (н1) в текущий момент времени t _н1 излучает сигнал запроса, спутник-ретранслятор (Р) в момент t _р1 ретранслирует сигнал запроса на космический аппарат (К), принятый на КА сигнал переизлучается в момент t _к (сигнал ответа), сигнал ответа ретранслируется спутником-ретранслятором в момент t _р2 и принимается наземным приемным пунктом (н2) в момент t _н2.

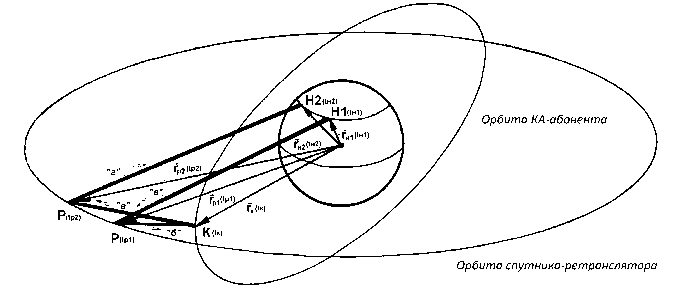
Схема распространения сигнала в радиолиниях космической системы ретрансляции

Положим, что на спутнике-ретрансляторе несущие частоты радиолиний Р → КА и Р → н2 формируются посредством гетеродинирования принимаемых сигналов и сигнала собственного задающего генератора, а несущая сигнала ответа КА когерентна частоте принимаемого КА сигнала. Обозначим частоту излучаемого с н1 сигнала запроса через

Чаплинский В.С. и др. Определение скоростных параметров...    19

ω = а ω . Переизлучаемый спутником-ретранслятором Р в момент t в сторону КА сигнал будет иметь частоту

ωр1(t) = ан1ωонАа(t) – вр1ωор(tр1), где А (t) – обобщенный функционал доплеровского и релятивистского преобразования сигнала в радиолинии «а» (н1 → Р), учитывающий также смещение частоты из-за распространения сигнала в тропосфере и ионосфере;

ω_он и ω_ор – эталонная частота задающего генератора (ЗГ) наземной станции и частота ЗГ спутника-ретранслятора в моменты t _н1 и t _р1 соответственно;

ан1 и вр1 – коэффициенты преобразования частот ЗГ наземной станции и спутника-ретранслятора при формировании несущих сигналов в радиолинии «а» и радиолинии «б» (Р → КА).

Принятый на КА сигнал переизлучается с несущей

ωк(t) = lан1ωон Ааб(t) – lвр1ωор(tр1)Аб(t), где l – коэффициент когерентного преобразования частоты;

А_аб( t ) и А_б( t ) – обобщенный функционал преобразования сигнала в радиолиниях «аб» (н1 → Р → КА) и в радиолинии «б» соответственно принимается спутником-ретранслятором в момент t _р2 и pетpaнслиpуeтся с несущей

ωр2(t) = вр2ωор(tр2) + lан1ωон Аабв(t) – lвр1ωор(tр1)Абв(t), где в – коэффициент преобразования частоты ЗГ ретранслятора при формировании несущей радиолинии «г» (Р → н2);

А_абв( t ) и А_бв( t ) – обобщенный функционал преобразования сигнала в радиолиниях «абв» (н1 → Р → КA → Р) и в радиолиниях «бв» (Р → КA → Р) соответственно.

Наземный приемный пункт будет иметь на входе ретранслированный сигнал ответа с несущей ω_н2/р( t ) = в_р2ω_ор( t _р2)А_г( t ) – l а_н1ω_онА_абвг( t ) + l в_р1ω_ор( t _р1)А_бвг( t ), где А_г( t ), А_абвг( t ) и А ( t ) – обобщенный функционал преобразования сигнала в радиолинии «г», радиолиниях «абвг» (н1 → Р → КA → Р → н2) и радиолиниях «бвг»(Р → КA → Р → н2) соответственно.

На приемном пункте н2 производится измерение смещения частоты принятого сигнала от опорного. Частота опорного сигнала ω_{н2 =} а_н2ω_он, где а_н2 – коэффициент преобразования. Мерный интервал T _н2 формируется от ЗГ наземной станции.

Результат измерения:

t н2н + ^Т н2

N - / tн2н

^ н2 ^ н2/ Р ( t ) d ^тн2 = ^ан2 ^ он Т н2 ( 1 а₂^Аабвг )

—

в р2

а н2 ω он Т н2

t н2н + Т н2

I tн 2 н

^ ор ( t р 2 ) А г ( t ) d Т н2 ^—

в р1 а н2 ω он Т н2

t н2н + Т н2

I tн2н

ω ор ( t р1 )А бвг ( t )dτ н2

где t _н2н – фиксируемый момент начала мерного интервала;

t н2н + ^Т н2

А абвг =             А абвг ( t )d ^тн2

Т н2

Выпуск 3/2019

является функцией отношения частот, несущих навигационную информацию, и, кроме того, содержит неопределенность, обусловленную реальным отличием частоты ЗГ ретранслятора в текущие моменты tр1 и tр2 от частоты ЗГ наземного пункта. Положим, что для ослабления влияния неопределенности частоты задающего генepaтopа спутника-ретранслятора с него излучается пилот-сигнал с частотой Шр(t) = аn«Op(t), где ап -коэффициент преобразования, который принимается наземным пунктом н2. На пункте н2 в общем случае производится измерение отклонения частоты принятого пилот-сиг- нала от опорного, сформированного от задающего генератора наземного пункта, на мерном интервале [ t н2н, t н2н+тн2 ] и мерном интервале [ t н2н - тбв, tн2н - Тбв + Т^ ], где тбв = tр2 - tpl,

t н2н + Т н2

N пс1=  J tн2н

а п ^ он

^ап^шор⁽ t p2^)Ar⁽ t ) d ^тн2 ,

t н2н ^Тбв + ^Тн2

N пс2 = f t н2н — Тбв

апшон

а_пω_ор( t p2K ( t ) | d Т_Н 2 .

Отсчеты N _пс1 и N _пс2 используются совместно с результатами измерений N для определения навигационного параметра. Выразим (1) через навигационные величины. Период колебаний принятого сигнала по собственному времени приемного пункта δτ_н2 и координатному времени δ t _н2 связан формулой

^ ^Т н 1 =^{[ 1   R} h 1 ⁽ t H 1 ) ^] £ t H 1 ,

^1⁽ t н1 ) ^фн1⁽ t н1 )

^где R н1⁽ t н1 ) =     --- 2 .

2 с          с

Момент приема на пункте н2 сигнала ответа t _н2 является функцией момента излучения с пункта н1 сигнала запроса t _н1, так что

δ t н2 = ^{dt н2} δ t н1 . dt _н1

С учетом (5)–(7)

д     _ ^Ыон^Аабвг⁽ t ) _ ^St h1 _ ^1- R н1⁽ t н1 ) ⁸ t H 1

^{А абВ} г        " он        ⁸ Т н2     I - К н2 ( t н2 ) S t H 2 ^.

Производную ^н1 найдем из операционного времени распространения сигнала dt _н2

t н2

—

t н1 = ¹ [ ( L а + L б + L в + L г ) ] ,

где с – скорость распространения радиоволн в свободном пространстве.

Тогда

= 1 — ^ н!

абвг   1 _— r

—

1 — R hi

c

Z L i , i

Чаплинский В.С. и др. Определение скоростных параметров...

где Rн1 и Rн2 – некоторые значения функций Rн1(tн1) и Rн2(tн2), принадлежащие мерному интервалу Tн2:

t h2+T н2

L i = I¹" J ^T_H2.

T н 2          τ н2

t н2н

С погрешностью в определяемой суммарной скорости не более 10–5 м/с для призем- ной области можно принять

А абвг =1 ^- 1 ^[ ( ^L а ^{+ L}6 ^{+ L} в ^{+ L} г ) ] .

Формула (12) дает связь суммарного скоростного навигационного параметра ∑ L_i со значением A абвг , функцией которого является непосредственное измерение. Среднее н а мерном интервале значение суммарного скоростного навигационного параметра ∑ L_i

выражается через приращение суммарной дальности _        t h2 + T „2

i

^ L i = t н2

J dd" L . ( t pl. t Hi ) + L б ( t k ,t pl ) + L . ( t p2 , t k ) + L г ( t н2 , ‘ р2 > d Т н. 13

t н2н

н2

Проведя аналогичные преобразования, получим

А бвг = ¹ - С ^[ L 6 ⁺ L в ⁺ L г ] ;

A _r( t ) = 1 - C L _r( t ).

Получим соотношения связи результатов измерений с навигационным параметром. Используя (10), (13)–(14), запишем (1) в виде

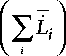
N    _ 1 + ^{1 а}н1 - ^{1 а}н1 1

ан2 ωонTн 2        ан2 ан2 с tн2н +Т н2

--р^Г-   J   wop( tp 1)A rd Th 2H р"1 ^L + ан2“онТн2            ор р2    г Н2 ан2 с I ^ q I

k q 7

tн2н tн2н +Tн2

+Y1 - а -^ РТН1    ^ “оР(tР1)]1 -7L(t)| ^Тн2, н2 он н2

t н2н

• 1    вр1 11Т I

где q = б, в; Y 1 = ан^^ I X 1- q .

• ^н V q 7

Из (3) следует, что t н2н + Тн2

N

J    « ор⁽ t pl)^Ar^{(t)d т}н2 = “ он ^Т н2 а .                   (17)

t н2н

Полученное значение (17) может непосредственно заменить первый интеграл в правой части выражения (16). С учетом (16) интерпретируем отсчет (4):

^ пс2   а п “ он ^Т н2 а п I 2 ,

где	_               t н2н Тбв + Т н2 I 2 = “ ор1 Т н2 - “ ор1 "TL( ^ г); Ь*г = Т^     J      [ L г ( 1 ) ] d Т н2 .      (19) t н2н - Тбв

22 в ыпуск 3/2019

Представим

t н2н + Тн2 где Lг = ТНГ  J tн2н

L г ( t )

l ; = ( L г ) -A L г ,

d ^тн2 ; ^L г — ( L г ) ( L г ) .

Подставим (20) в (19). Тогда

1 2 - ^ ор Т н². Д L г = ^_ор1 Т _Н 2 - „_ор1 Т н^ ( L г ) .

С другой стороны, второй интеграл в правой части выражения (16)

t н2н + ^Тн2 ) t н2н

" ор⁽ t pl ) ! ¹ - 1 [ L г⁽ t ) ] } d ^тн2 =" ор1 ^Т н2 ^- " ор1 Т Т" ( L г )

равен выражению (21). Следовательно,

I 2 ^-

ω ор1 Т н 2 с

^A L г = ( « он ^Т н2 ^-

N

пс2

а

п

)

^р ' "' A L _г. с ^г

Выполнив замены в (16) интегралов через результаты измерения пилот-сигнала (17) и

(22), получим

--N^ = 1 + ^ан- - ^ан111 X Ье |+М —N^--1) + i н2 он н2          н2 н2                   н2 п он н2

i

+ l B pl l [у L |+ ^{1 В}р1     N пс2

^ан2 с I ^X q I ^ан2 ^{( а}п“» ^Т21 \ q 7

^- 1 ) ⁺ Y 1 +Y 1 ,

где γ

l ^вр1 ^ыор1 A t г а н2 ω он    с .

Выделим в (23) определяемые навигационные величины

L 6 ⁺ L в ) ⁺ ТН1 - _; р _Г ⁽ L а ⁺ L г ) = =

l а н1 ^+ан2    , _с ^ВР² (    N пс1    _— 1 \ ,

¹ ( а н1 ^{— В}р1 )      ¹ ( а н1 ^{— В}р1 ) а ^п “ ^{он Т н2}

, с

вр1

а н1 ^{— В}р1

^N пс2

⁽ а п “ он ^Т н2

—

с

N

“ он ^Тн2¹ ( ^ан1 ^{— В}р1 )

,

+— в р¹— A L _г + ^{В р}1 ^Л“ о^Р1 f L_fl ) . ^ан1 ^{— В}р1 г ^ан1 ^{— В}р1 “ он I ^ q I

V q /

Скоростной навигационный параметр

Чаплинский В.С. и др. Определение скоростных параметров... 23

В правой части формулы (24) слагаемое вр1 ALг < вр1 • 0,25 •IO-3 м/с ан1- вр1 г ан1- вр1

^п Р ^и L гмакс ^ ^{40 м/с} и ^т бв = 1 ( L б + L в ) ” ^0,25 с, в зависимости от требований по точности и соотношения частот в радиоли н иях, либо опускается, либо вводится в виде поправки на основе прогноза величины ∆ L _г . Последнее слагаемое, зависящее от относительной разности ДЗЧ задающих генераторов спутника-ретранслятора и наземного пункта, опускается, составляя тем самым пренебрежимую методическую погрешность. Полученный по результатам измерений в ретрансляционной радиолинии суммарно-скоростной навигационный параметр (25) по своей сути является интегральным, характеризующим приращение суммарной дальности на интервале измерения Т_н2.

Заключение

Функциональная задача навигационных измерений несущественно усложняет техническое построение ретрансляционного радиотехнического комплекса, а при определении скоростных параметров по доплеровскому смещению несущих частот радиосигналов не ухудшает энергетический потенциал радиолиний при информационном обмене с КА-абонентами. В то же время достаточно высокая информативность ретрансляционных измерений позволяет осуществлять навигационный контроль КА без ограничений, присущих наземному комплексу управления со средствами непосредственной связи с КА, и тем самым определяет очевидную целесообразность включения задачи навигационных измерений в состав функций ретрансляционных систем информационного обмена с КА.

Проведенная математическая интерпретация измерительной информации иллюстрирует характерную аппаратурную зависимость результатов скоростных измерений, которая должна учитываться при траекторном контроле КА-абонентов космических систем ретрансляции.