Определение средней длины очереди СМО через корреляционные моменты числа заявок на интервалах обслуживания
Автор: Лихтциндер Борис Яковлевич, Макаров Игорь Сергеевич
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии компьютерных систем и сетей
Статья в выпуске: 1 т.9, 2011 года.
Бесплатный доступ
В статье рассматривается стационарный ординарный поток заявок, поступающих на обработку в систему массового обслуживания (СМО). Определяется средняя доля недообслуживания через корреляционные моменты числа заявок на интервалах обслуживания.
Система массового обслуживания, теория массового обслуживания, анализ трафика, взаимная корреляция, полиномиальная аппроксимация, мультиплексирование
Короткий адрес: https://sciup.org/140191452
IDR: 140191452 | УДК: 621.391
Текст научной статьи Определение средней длины очереди СМО через корреляционные моменты числа заявок на интервалах обслуживания
Рассматривается стационарный ординарный поток заявок, поступающих на обработку в СМО.
Допустим, что каждая заявка обрабатывается в течение постоянного времени т .
Разделим весь рассматриваемый интервал времени на N одинаковых промежутков длительностью г . Порядковый номер промежутков обозначим через Z . Вследствие ординарности потоков заявок в течение каждого Z -го промежутка времени поступает целое число заявок WiW (= 0; 1; 2…). Следовательно, число заявок, поступающих в течение времени т , является дискретной случайной величиной с математическим о жида нием m^ , вторым начальным моментом w2 (г) и дисперсией 7)m(r).
В течение каждого z -го промежутка времени в СМО находится Qi^ заявок, ожидающих в очереди. Длина очереди также является дискретной случайной величиной с математическим ожиданием q^ .
Обозначим через Qi-j^ последовательность случайных чисел, сдвинутую относительно Qi^ на j промежутков т .
Взаимныекорреляционные моменты
Определим вторые взаимные начальные моменты последовательностей m,^ и Qi-j^ как математические ожидания произведений их соответствующих элементов:
vq,^4HlTW\ У=0;1;2... (1)
Вторые взаимные центральные моменты указанных последовательностей, называемые корреляционными моментами, или ковариацией, определяются как математические ожидания произведений центрированных значений их элементов:
Pq m M = Vq.-i^ - 7(r)] • [zw;(r) - m^"\, . (2)
j=0;l;2...
Между указанными моментами существует известное соотношение
Vq.-,™, ^ = ^4,-, ^ + Ч^МТ)- (3)
Уравнение баланса
Для любой одноприборной СМО справедливо рекуррентное соотношение, устанавливающее связь между поступающими и обработанными заявками:
qi^-q^^ + m^^-S^Ty, (4)
o, ^(Г) = 1 л
если qj4 (r) = m/ (r) = 0; в противном случае.
Обратим внимание на особенности :
З^З^т);
З^т^т) = т^т); (6)
8i^ = 3i^qi_^ = qi_^Ty
Предпоследнее равенство легко получить, найдя математическое ожидание левой и правой частей (4). Далее выполним следующее преобразование соотношения (4). Умножим его левую и правую части на т^ , а затем найдем математическое ожидание от обеих частей:
q^m^T) = q^^rn^T) + т2 (г) - З^т^т), и с учетом (Г); (3) и (6) получим т2 (г) - ш(г) = /л^ (г) - ц^,, (г). (7)
Соотношение (7) справедливо для любого закона распределения вероятностей числа заявок, поступающих в течение промежутков времени г.
Среднее значение длины очереди
Далее произведем еще одно тождественное преобразование (4), для чего возведем обе части равенства в квадрат и найдем математические ожидания полученных выражений. После соответствующих преобразований получим
—— m2(r)-m(r)
q^=— 2 + уЧм™. ^-
С учетом (7) и (3) после преобразований получим:
— _ ИЧ№ М + Hq^m, (г) Ц\Т) — ----
2[1 - т(г)]
Соотношение (8) обобщает формулу Хинчи-на-Поллачека [1] для стационарных, ординарных потоков заявок и устанавливает зависимость средней длины очереди от вторых взаимных центральных моментов.
Если поток заявок имеет параметр интенсивности X , то при пос тоянн ом времени обслуживания т имеет место т^ = Хт вне зависимости закона распределения потока.
В результате получим
4 2(1 -Хт)
да
/ х ^Qimi ^^ ~*~ ^/-iw< ^^
Обозначим окончательно и тог-
^Т Mqm<^ q^= '
1 -Хт
Зависимость ^qm^ приводится к виду
„ zxMfWi-iOJwdllzZ!^
Обозначим цент рированные значения числа ______ 0
заявок т,(т) - т(т) = т^т) и преобразуем выра жение к виду
Mq,A^ = ^ Wj.j (r) nij (r) - ^ З,. , (г) пт, (r) + m^T^m^r)-З^т^т^т)
mi^ на каждом интервале т и определения значений q.^ по формуле (4). На рис. 1 показаны функции распределения вероятностей интервалов vi между соседними заявками для потоков с Г- распределением.
Все потоки имеют одинаковые значения пара-„ 1 й метра интенсивности X = = , где 9 – математи ческое ожидание интервалов между соседними заявками. Потоки имеют различные значения коэффициентов вариации S^ интервалов между соседними заявками. Для потоков с экспоненциальным распределением интервалов ^s -1 .
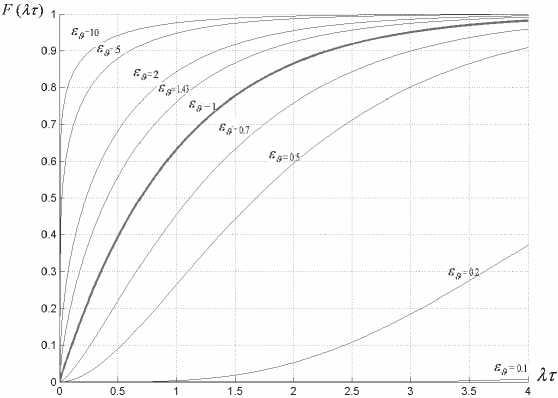
Рис. 1. Функции распределения вероятностей интервалов Vj
Подставив Mqm^ в (10), получим формулу Хинчина-Поллачека для экспоненциальных потоков. Зависимости, показанные на рис. 2, хорошо поддаются полиномиальной аппроксимации. Полученные при этом коэффициенты полностью характеризуют поток заявок с точки зрения средних значений очереди, возникающей при их обработке.
Полиномиальная аппроксимация
Анализ графиков функции Mqm^ показывает, что:
-
- указанная функция не имеет отрицательных значений;
-
- для пуассоновского потока заявок график функции имеет вид параболы;
-
- значение функции MqM для потоков заявок с коэффициентом вариации интервалов между заявками ^,9 > 1 превышает значения этой функции для пуассоновского закона;
-
- для потоков заявок с высокой степенью детерминированности (^<1) в начальном диапазоне изменения Xt функция Pqm^ имеет весьма малые значения.
Поскольку функция «(Г) в соотношении (14) изменяется незначительно, предполагается аппроксимировать функцию Pqm^) полиномом второй степени с ограничениями.
^Xff +(«-l)2r
Mqm^ = <
X
если
О, если Лт<(1-а).
Лт>(1—ск);
На рис. 2 показаны зависимости Mq.A^ для соответствующих потоков заявок. Кривая Mq^ , соответствующая экспоненциальному распределению интервалов (пуассоновский поток), показанная на рис. 2, имеет вид параболы
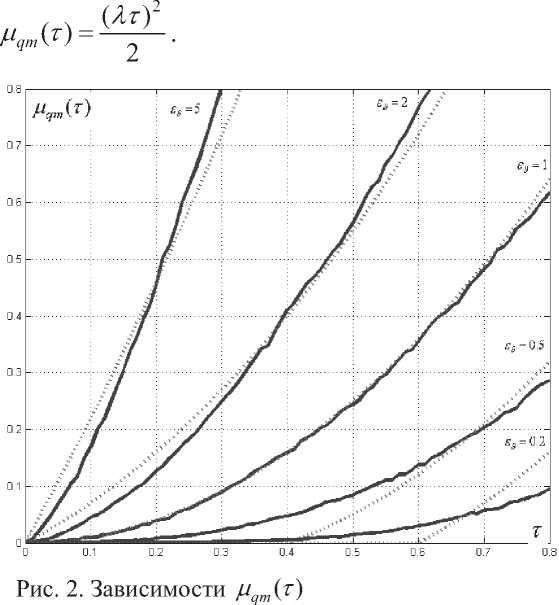
Коэффициент а указывает на степень отличия потоков заявок от пуассоновского. Для пуассоновского потока коэффициент а = 1 . Для потоков с высоким коэффициентом вариации (^>1) интервалов между соседними заявками (пачечные потоки) коэффициент а больше нуля и условие Хт > (1 -а) выполняется во всем диапазоне изменения Хт . Для потоков с высокой степенью детерминированности (£5<1) коэффициент а имеет отрицательные значения (О < а < 1) и функция Mqrn^ равна нулю, в диапазоне изменения Хт от нуля до -^тах ^ 1-«.
На рис. 2 пунктиром показаны графики, аппроксимирующие Mqm<^ , полученные по методу наименьших квадратов. Отрицательные области исключаются в соответствии с ограничениями (15).
Ниже приведена таблица значений коэффициента Ct для соответствующих графиков.
Таблица 1. Значения коэффициента a
|
Ev |
0,2 |
0,5 |
1 |
2 |
5 |
|
а |
3,1 |
1,7 |
1 |
0,6 |
0,3 |
Таким образом, полученный экспериментальным путем коэффициент a совместно с параметром потока X полностью характеризует стационарный поток заявок общего вида с точки зрения средних значений очередей, возникающих в одноканальной СМО с постоянным временем обработки т .
Для потоков заявок с высокой степенью вариации интервалов между соседними заявками во всем диапазоне изменения значений Xt справедливо соотношение, обобщающее формулу Хин-чина-Поллачека:
q<^ = ^^-7-^-7^- ■ (16)
2(1-Яг)
Формула (16) справедлива для СМО с постоянным временем т обслуживания заявок.
Если время обслуживания является случайной величиной, то следует использовать значения ее первого и второго начального моментов :
- Xi r2 + (а -1)Яг q =---------=----
2(1-Яг)
Соотношение (17) определяет среднюю длину очереди в одноприборной СМО с заданным распределением вероятностей времени обслуживания.
Мультиплексирование потоков
Допустим, что рассматриваемый поток заявок состоит из К независимых потоков с номерами к (k = \,K) . Время обработки любой из заявок постоянно и равно т .
Обозначим через mkl^ число заявок k-го по-к тока на интервале i . Очевидно, что т^ - ^mkj .
k=1
Математическое ожидание числа заявок в суммарном потоке т,.(г) = ^тА.(г) = Яг,
^=1
где Я=Е^
– суммарная интенсивность пото- ка. Поскольку составляющие потока взаимно не- зависимы, выполняются соотношения:
Dm W = E Dk»M, k-^ = E ^kmm ^ k=\ k=l где Dkm^ – дисперсия числа заявок на интервале г для k -го потока;
О) о
Mkmm^ = Е^!/^)^-^) – суммарный ко эффициент ковариации для k-го потока.
Из (14) непосредственно следует, что «(г)Яг = Z)„,(r) + 2^mm(r). Подставив значения Dm^ И PmnA^, получаем а<т>Хт = Е VDkm (г) + 2цктт (г)] ,
Dkm <Л) + ^Мктт (^) 4^
По аналогии с (14) обозначим содержимое в квадратных скобках через :
a(r) = Е “к^^Т"- (18)
к=\
Функции «кк^ изменяются незначительно, и во всем диапазоне изменения Хт могут быть заменены их средними значениями ^к . Тогда после подстановки в (16) получим для суммарного потока
CL^y ^ q(r) = ^-----------------. (19) 2(1-ЕЛ^) 4=1 Если различные типы заявок имеют различное время обслуживания ^" к , то для определения среднего значения очереди можно воспользоваться соотношением (17), где Тк „ ’ 7 —/ ,Т к ] ’ 4=1 4=1 Предложенная методика экспериментального исследования случайных потоков заявок позволяет, помимо параметра интенсивности потока Я , определить значение параметра а , характеризующего степень отличия потока от пуассоновского. Указанный параметр может быть использован в обобщенной формуле Хинчина-Поллачека при вычислении средних значений длины в одноприборной СМО.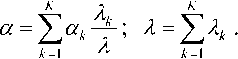
Список литературы Определение средней длины очереди СМО через корреляционные моменты числа заявок на интервалах обслуживания
- Клейнрок Л. Теория массового обслуживания. М.: Машиностроение, 1979. -432 с.


