Определение структуры линейного динамического объекта в задачах непараметрической идентификации

Введение. Одной из основных проблем современной теории идентификации и управления является определение структуры модели исследуемого объекта. На сегодняшний день большинство работ по данной проблеме посвящены методам параметрической идентификации [1–3], где структура процесса постулируется с точность до вектора параметров, исходя из имеющейся априорной информации. Причем выбор структуры модели процесса основывается на накопленном опыте работы с подобными объектами, а также зачастую осуществляется методом перебора различных моделей из заданного класса. Далее следует этап настройки параметров модели с использованием различных математических подходов, таких как, например, метод наименьших квадратов, различные рекуррентные оценки и т. д. В условиях недостатка априорной информации об объекте исследования такие подходы малоэффективны из-за наличия существующего многообразия процессов, их сложности и малоизученности.

В научной литературе по данной проблематике можно выделить несколько подходов. Рассмотрим наиболее известные из них. В работе [4] предлагается метод восстановления модели, в котором сначала следует этап выбора предполагаемой структуры из априорной информации, настройка параметров модели с использованием рекуррентных методов, а далее на основе имеющейся выборки измерений выполняется проверка предложенной модели. В случае получения неудовлетворительных результатов моделирования структура модели подлежит доработке, а параметры модели настраиваются заново. Как отмечалось ранее, подавляющее большинство подходов в задачах выбора параметрической структуры модели основаны на переборных методах, к которым относится, в частности, метод группового учета аргументов [5; 6]. Сущность метода состоит в выборе регрессионных моделей оптимальной сложности, где под сложностью понимается число параметров модели. Таким образом, в рамках данного метода осуществляется перебор многих моделей-претендентов с различным числом параметров по ряду критериев. В результате находится модель оптимальной структуры в виде одного уравнения или системы уравнений [5]. В [7] излагаются методы структурной идентификации динамических систем на основе анализа информационных портретов. Предложена процедура нахождения порядка модели, основанная на минимизации ширины интервала изменения коэффициента структурности [7]. В настоящей статье предполагается новый метод определения структуры линейного динамического объекта, основанный на непараметрической теории идентификации [8–10]. В основу предлагаемого метода ложится правило выделения существенных переменных на основе измерения коэффициента размытости ядерной функции в непараметрической модели. Впервые данная идея была предложена профессором А. В. Медведевым в [11].

Постановка задачи идентификации . Пусть объект представляет собой одномерную динамическую систему и описывается следующим разностным уравнением:

xt = f ( x t - 1 , x t - 2 , -, x t - k , ut ), ⁽¹⁾ где f ( . ) – неизвестный функционал; x_t – выходная переменная процесса; u_t – управляющее воздействие; k – глубина памяти динамического объекта (в терминологии А. А. Фельдбаума) [12]. Если проводить аналогию с описанием исследуемого процесса в непрерывном времени в виде дифференциальных уравнений, то k – порядок старшей производной в соответствующем уравнении. Здесь существенным является то, что вид функционала не определен с точностью до параметров.

Классическая для теории идентификации блок-схема моделирования данного процесса представлена на рис. 1.

На рис. 1 приняты следующие обозначения: x_s ( t ) – выход модели объекта; ( t ) – непрерывное время; индекс t – дискретное время; h_t^u , h_t^x – случайные помехи измерений соответствующих переменных процесса; индекс h у переменных объекта из соображения простоты опущен: u t = u h , x_t = x h ; ^ ( t ) - векторная случайная помеха.

Введем обозначения:

zt =( zi,-, zk+1 ) = ( xt-1,-> xt - k, U), тогда xt = f (zt) ■

При идентификации динамической системы (1) ее параметрическую модель естественно принять в форме xs = fs (Xt-1, —, Xt-k, U,a),( где a - вектор параметров, подлежащий оцениванию на основании обучающей выборки. Таким образом в случае линейной динамической системы определение структуры динамического объекта (1) сводится к определению переменных, входящих в состав модели (4). C учетом переобозначений (2) модель (4) может быть показана на схеме (рис. 2), которая иллюстрирует модель динамической системы в дискретном времени, сведенную к модели статической системы, когда на вход последней поступают не только пере-менныеut, но и xt-1,xt-2, ...,xt-k и т. д.

На рис. 2 ЭЗ - элемент запаздывания [1]. Схема, изображенная на рис. 2, также является близкой к классической схеме, рассматриваемой в теории (рис. 1), так как дискретное уравнение, описывающее объект в данном случае, имеет соответствующий аналог среди дифференциальных уравнений. Как было замечено ранее [13; 14], рассмотрение динамического процесса с помощью данной схемы не является единственным, так как одна из переменных процесса, например x_t _ ₂ , может отсутствовать, а конечное выходное воздействие может зависеть только от переменных x_{t -1} , x_{t -3} и входного воздействия u_t : x_t = f ( x_{t - 1}, x_{t - 3}, u_t ). Таким образом, схема примет вид, изображенный на рис. 3.

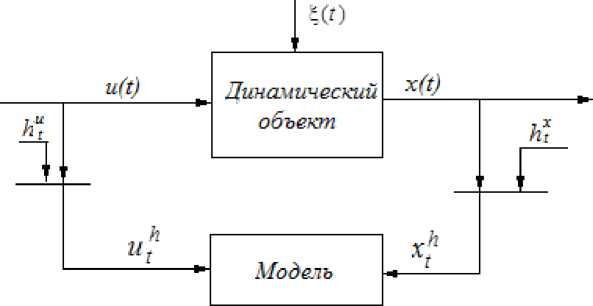
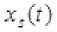
Рис. 1. Классическая схема моделирования одномерного динамического объекта

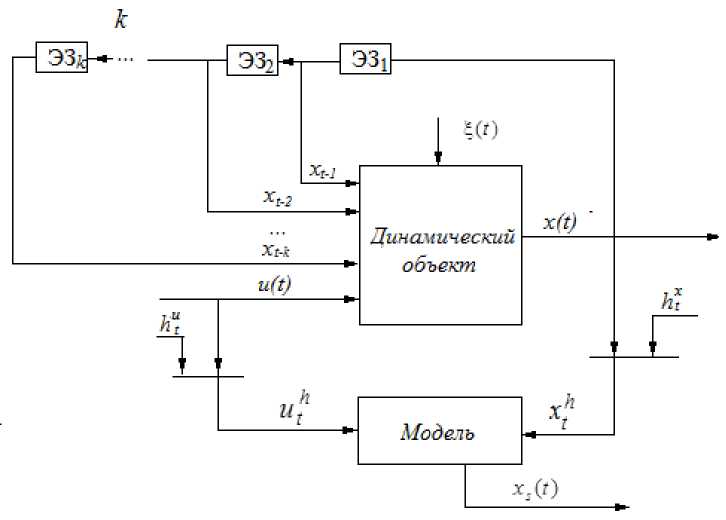
Рис. 2. Блок-схема моделирования объекта с памятью

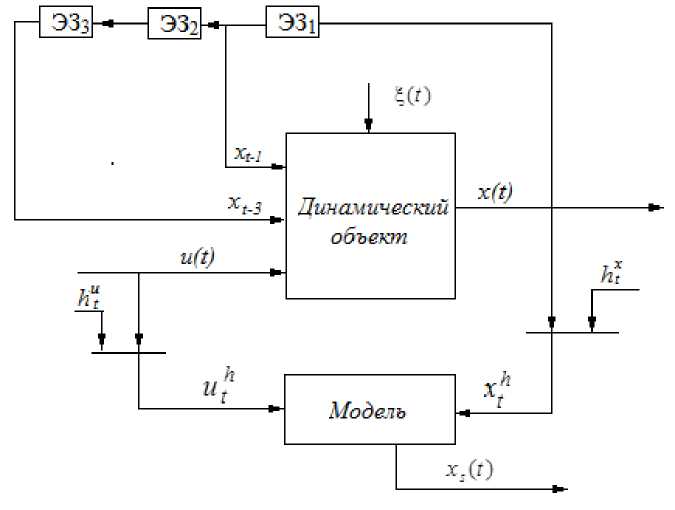
Рис. 3. Блок-схема моделирования объекта с памятью при фиксированных запаздывающих на соответствующие число тактов выходных переменных

В рассматриваемой задаче контроль входных-выходных переменных осуществляется через одинаковые интервалы времени A t. Производя соответствующие измерения, получаем исходную выборку входных-выходных переменных { x i , u i , i = 1, 5 }, где 5 -объем выборки. Задача состоит в определении запаздывающих на определенные такты выходных переменных, которые необходимо учесть в модели (4), что позволит сделать предположение о параметрической структуре модели динамического объекта (4).

Выделение существенных переменных. В классическом случае, изображённом на рис. 2, задача идентификации состоит в оценивании класса операторов на основе выборки {xi, ui, i = 1,5}. Таким образом, в качестве оценки модели объекта может быть принято условное математическое ожидание вида x (t) = M{ x (t)/u (t)}. (5)

-Z V H 5 i = 1

u

^^^^^^в

ui

u cs

■ 4" H сsx

xs^-x-L

X

X

X 4" H с s ^x

( xs-3 xi-3

X

В моделях (6), (7) H ( ■ ) - ядерная колоколообраз-

ная

1          jt функция, с5,с5 , ..., c5

тости ядерной функции, условиям сходимости [15].

- коэффициенты размы-которые удовлетворяют В качестве колоколооб-

В случае, когда динамический объект описывается дифференциальным уравнением при последовательной дискретизации, итоговое разностное уравнение будет содержать последовательно все переменные: x t - 1 , x t _{- 2}, ..., x t - k . Этому соответствует блок-схема моделирования, изображенная на рис. 2. Тогда в качестве непараметрической модели объекта можно использовать модель, в которой все коэффициенты разностного уравнения будут учтены [11]:

разной функции H ( ■ ) могут быть использованы различные ядра [15]. Следует учитывать, что модели вида (6), (7) можно использовать только при равных интервалах измерения A t .

* x ¹ * x ²

Оптимальные параметры размытости с ₅ , с ₅ , ...,

* xk                           -            „      - _ с 5 при наличии обучающей выборки находятся из задачи минимизации показателя соответствия выхода объекта xt и выхода модели x5, основанного на методе скользящего экзамена, когда в моделях (6), (7) по индексу г исключается q-е наблюдение переменной, предъявляемой для экзамена:

¹ *Y²           *Y^k

R ( с 5 , с 5 , ..., с 5

5                ²

) = Z(xq - xq )

xs

=-Z VH ⁵ i = 1

u

^^^^^^»

ui

u cs

k

П - j H j = 1 c x

(           А x5 - j — xi- j

x cs

1 1 х² xx

' 5 , ^С 5

min

,

x ^k

.., с 5

...

q = 1

, q * i ,

Для случая, изображенного на рис. 3, модель может быть принята в виде (7), где учтены только выходные переменные, непосредственно от которых зависит выход процесса:

где индекс i фигурирует в формулах (6), (7).

Существенным в оценках (6), (7) является то, что в соответствие каждой выходной переменной x₅ - 1 , ..., x₅ - _k , запаздывающей на некоторые величины,

ставится свой коэффициент

x1          xk csx, ..., csx

.

размытости ядра

Алгоритм вычисления значимых переменных x_s - j строится по следующей схеме. Сначала задаем

Из представленных выше моделей видно, что степень вклада той или иной выходной переменной из правой части уравнений в итоговое значение оценки зависит от

начальное значение k. Затем строим модель по формуле (6) и считаем относительную ошибку моделирования W ₀ :

1 _H c s ^{x j}

x s - j ^- x i - j

A

ss

-£( x - x ) ²/£ — ( m x - x )², ^stt        / и ^{s - 1}

Выражение (9) состоит из двух частей:

и

H

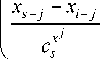
. Что касается первого множителя то

x^j c_s^x

x^j , c s ^x

наблюдается

следующая зависимость: чем

где m_x – математическое ожидание.

Далее на каждой i -й итерации выполняем следующий набор действий:

1 k

• 1.    Для каждого коэффициента c_s^x , ..., c_s^x нахо-

• x1*x1x2*x2

• 2.    Находим из всех полученных значений макси- x^j мальное – c .

дится оптимальное значение: cs = c s , cs = c s , ..., xk     *xk cs = c s .

max_ s

меньше

x^j                                                           1

csx , тем больший вклад значение j вносит x cs

3. Строим модель по формуле (6), исключая мно-

в итоговую оценку. Таким образом, можно построить

житель Н

x.

^- x i

c

'x-

A

при учете, что j – номер

следующую цепочку неравенств:

s

12 k если cs < cs <... < cs

то — > — x1x2 cscs

k . c s ^x

^j при c^x    .

max_ s

Рассмотрим вторую составляющую уравнения (9).

Коэффициенты c x и ядерная функция Н ( ■ ) должны удовлетворять следующему свойству:

c

w

JН

w

wi

's Q ( u )

w cs

¹w = 1,

где w – некоторая переменная. Исходя из данного x1*x1x2*x2         xk условия, при учете, что cs = c s , cs = c s , ..., cs = k

= c _s , можно построить следующую последователь-

4. Считаем относительную ошибку W_i .

Данные действия будут повторяться, пока W ^ W i. i         i - 1

Вычислительный эксперимент . Численное исследование алгоритма непараметрической идентификации осуществлялось методами статистического моделирования. Для вычислительного эксперимента был выбран объект, описываемый уравнением вида

0,5 d-x + 0,5 d-x + 0,8 dx + 1,5 x ( t ) = u ( t ).     (12)

dt ²        dt ² dt

ность неравенств:

В дискретном виде данное уравнение равно xt = 2,69 ■ xt-1 - 2,46 xt-2 + 0,73 xt-3 + 0,015 ut. (13)

*x1      *x2            *xk если c s < c s <... < c s , то

Г           A

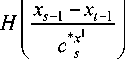
< Н

x s - 2 ^- x t - k

I c s

... <  Н

J

x s - k ^- x t - k

^k c ^* _s ^x

A

J

Приведем пример. Пусть c*sx1 – коэффициент раз- мытости ядра при xs-1, а c s - при xs-2. Если

cs

< ^c s

, то Н

x s - 1 ^- x t - 1

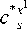
A            A

< Н

x s - 2 ^- x t - k

Зададим начальное значение k = 6. Результаты моделирования с использованием формулы (6) представлены на рис. 5.

Относительная ошибка моделирования W ₀ = 0,017. Далее находим оптимальные коэффициенты с использованием алгоритма покоординатного спуска. Найденные коэффициенты равны: с ** = 0,675 при u_t , с * = 0,131 при x_t _ 1 , с*₂ = 0,186 при x_{t - 2}, с ** = 0,412 при x_t - 3 , с ** = 1,023 при x_t - 4 , с 6 = 1,988 при x_t - 5 ,

V

² c_s^x

J

, и тогда

*

с ₇ = 1,876 при x_{t - 6}. Зависимость между полученны-

выходная переменная x_s - 1 имеет большее влияние

ми коэффициентами и значениями колоколообразной

функции представлены на рис. 6.

на выходную величину, чем x_{s - 2}. Графически это выражается так, как показано на рис. 4.

На рис. 4

На рис. 6

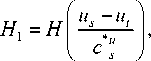
Н 7

= Н

x s - 1 ^- x t - 1

Н 1

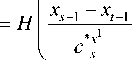
, Н 2 = Н

x s - 2 ^- x t - k

* x ²

V c s

A

x s - 6 ^- xt - 6

J

После выполнения всех этапов алгоритма были исключены переменные x_t - 4 , x_{t - 5}, x_{t - 6}. Таким образом, полученная итоговая структура динамического объекта, описываемого дифференциальным уравнением третьего порядка (12), равна:

xs = а1 xt-1 + а2xt-2 + «3xt-3 + Р ut, что соответствует структуре разностного уравнения объекта (13), а непараметрическая модель имеет вид

xs

x ² с_s

x s - 2 ^- Х - 2

x ² c_s

■ 4 Ф с_s^x

x ³ с_s

x s - 1 ^- Х - 1

x cs

x s - 3 ^- X - 3

V

x ³ c_s

X

Результаты моделирования с использованием формулы (14) представлены на рис. 7.

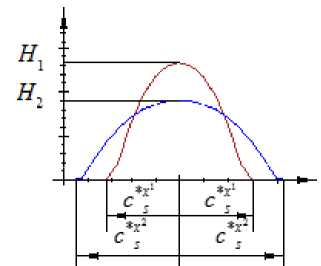
Рис. 4. Зависимость величины значения ядерной колоколообразной функции от величины коэффициента размытости ядра

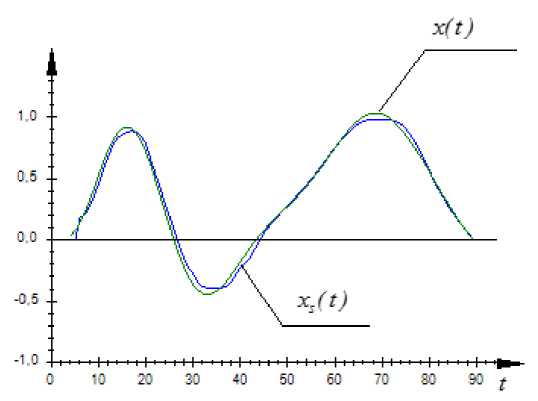
Рис. 5. Результаты моделирования процесса (13) при значении k = 6

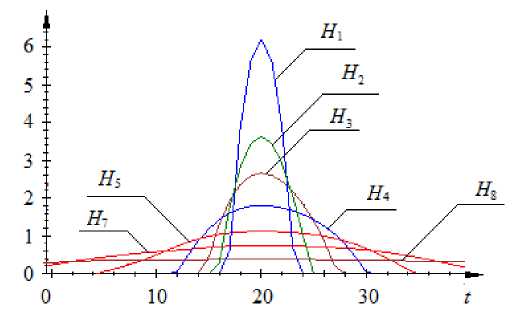
Рис. 6. Зависимость величины значений ядерной колоколообразной функции

* u * x ¹ * x ⁶

от величин полученных оптимальных коэффициентов размытости ядра с ^u _sc_s ^x , ..., c_s ^x

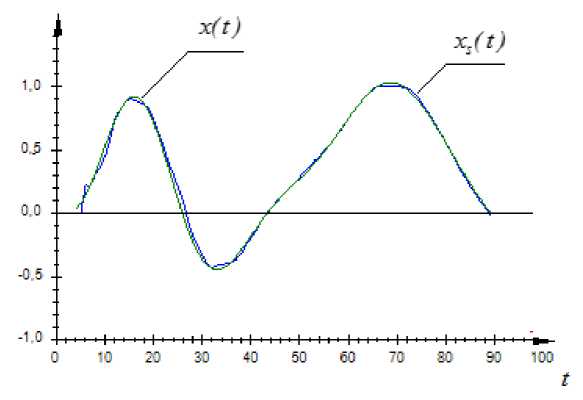
Рис. 7. Результаты моделирования процесса (13) при использовании модели (14)

Относительная ошибка моделирования равна W 3 = 0,005.

Рассмотрим процесс восстановления структуры модели для объекта с памятью. Пусть объект описывается следующим дискретным уравнением:

x t = 0,2 ■ x t - 1 + 0,4 x t _ 3 + 0,5 u t .            (15)

Выберем в качестве начального значения k = 4. Относительная ошибка моделирования, полученная на первой итерации, равна W0 = 0,105. Далее следует этап нахождения оптимальных коэффициентов: с4 = 0,124 при ut, с* = 0,231 при xt_1, с * = 0,393 при xt_2, с3 = 0,129 при xt_3, с5 = 0,425 при xt_4. После исключения переменных xt_2 и xt_4 относительная ошибка моделирования сократилась до W2 = = 0,012, а параметрическая структура была найдена в виде xs =а1 xt-1 +а2xt-3 +в ut, что соответствует структуре дискретного уравнения (15).

Заключение. В статье предложен алгоритм определения параметрической структуры линейного динамического объекта, основанный на применении правила выделения существенных переменных. Данный подход тесно связан с определением оптимальных коэффициентов размытости ядерной функции при использовании непараметрической модели функции регрессии по наблюдениям. В статье предлагается алгоритм, действие которого сводится к определению глубины памяти динамического объекта, которая представляет собой порядок старшей производной в соответствующем дифференциальном уравнении при проведении аналогии с описанием исследуемого процесса в непрерывном времени. Данный алгоритм состоит из нескольких этапов, включающих в себя определение оптимальных коэффициентов размытости, их отбор и построение итоговой модели. Одним из основных преимуществ предложенного алгоритма по сравнению с доминирующими на сегодняшней день методами восстановления параметрической структуры является тот факт, что разработанный непараметрический алгоритм более применим к задачам практики, так как способен работать в условиях малой априорной информации об объекте.

Acknowledgments . I would like to express my gratitude to Prof. A. V. Medvedev for continuous guidance and research assistance.