Определение технологических параметров систем замораживания пород из условия поддержания проектной толщины ледопородного ограждения

Строительство шахтных стволов в обводненных грунтах и породах осуществляется с использованием специальных способов. Одним из наиболее распространенных специальных способов при строительстве стволов калийных рудников является искусственное замораживание пород [1, 2]. Целью искусственного замораживания является формирование вокруг строящегося ствола временного ледопородного ограждения (ЛПО), препятствующего проникновению подземных вод в ствол и повышающего прочность горных пород в окрестности незакреплённых стенок ствола до возведения постоянной крепи [3–5].

Проходка шахтного ствола начинается только после образования замкнутого контура ЛПО с проектной толщиной, которая определяется исходя из условий прочности и ползучести [6, 7]. Расчет ЛПО на прочность и ползучесть, как правило, осуществляется для определенной однородной отрицательной температуры слагающих его горных пород [8]. Поскольку на практике распределение температур в объеме ЛПО неоднородно, то важным вопросом при определении https://mst.misis.ru/

2021;6(3):192–202

толщины ЛПО по рассчитанному полю температур является выбор изотерм, которые соответствуют границам ЛПО. На практике как правило, применяют два типа изотерм [5]:

• 1)    температура фактического замерзания воды в порах (около 0 °С);

• 2)    температура, при которой измерялись прочностные и реологические свойства замораживаемых пород (–4 … –12 °С).

На основании представленной в литературе информации об искусственном замораживании пород [3, 5, 9], можно принять, что оба способа выбора граничных изотерм ЛПО применимы на стадии активного замораживания породного массива, когда температура замораживающего рассола принимает минимальные значения, а расход рассола – максимальные значения. Однако в работе [5] было показано, что на стадии пассивного замораживания с более высокими температурами и более низкими расходами рассола, может происходить временное уменьшение толщин ЛПО до значений, ниже минимально-допустимых из условий прочности и ползучести. В большей степени такое снижение толщины ЛПО характерно для второго способа выбора граничных изотерм ЛПО. Снижение толщины ЛПО наблюдается при пассивном замораживании как в нормальном режиме работы замораживающей станции, так и в аварийном режиме, который может заключаться в выходе из строя одной или нескольких замораживающих колонок [10].

Другой важный вопрос – это выбор расстояния между соседними замораживающими колонками и, как следствие, общего количества замораживающих колонок [11–14]. Вопрос изменения толщины ЛПО на стадии пассивного замораживания, рассчитанной при различных расстояниях между замораживающими колонками, недостаточно исследован в существующей российской и зарубежной литературе. Данный вопрос является актуальным с точки зрения обеспечения надежности ЛПО и безопасности ведения горных работ в строящихся стволах с применением технологии искусственного замораживания.

Настоящая работа продолжает исследования, представленные в статье [5]. Целью как предшествующей, так и настоящей статьи, являлось проведение теплотехнического расчета ЛПО с последующим теоретическим анализом изменения толщины ЛПО при переходе на стадию пассивного замораживания. В предыдущей работе [5] акцент был сделан на проведении сравнительного анализа рассчитанных толщин ЛПО по различным изотермам и зависимости уменьшения толщины ЛПО на стадии пассивного замораживания. В настоящей статье сделана попытка углубить и продолжить сделанный ранее анализ динамики толщины ЛПО на стадии пассивного замораживания. Особое внимание уделено влиянию длительности стадии активного замораживания и расстояния между колонками на состояние ЛПО. Идея исследования заключается в определении этих технологических параметров исходя из условия поддержания проектной толщины ЛПО на стадии пассивного замораживания.

Математическая модель

Рассматривается задача о замораживании породного массива круговым контуром замораживающих коронок по рассольной схеме. Предполагается, что следующие физические процессы играют существенную роль при формировании ЛПО в породном массиве [15]:

• 1)    кондуктивный теплоперенос (теплопроводность);

• 2)    фазовый переход воды в порах массива;

• 3)    теплообмен между породным массивом и рассолом, циркулирующим в колонках.

В результате движения рассола с отрицательной температурой по замораживающим колонкам окружающий породный массив постепенно охлаждается и замораживается. В нем формируется зона льда, где поровая вода считается полностью замерзшей, и зона охлаждения, в которой породный массив не заморожен, но имеет более низкую температуру, чем в естественных условиях на рассматриваемой глубине. Между зоной льда и зоной охлаждения также иногда выделяют так называемую переходную зону (mushy zone), где одновременно присутствуют лед и вода [16, 17].

При моделировании теплопереноса в замораживаемом породном массиве принимается следующий список упрощений:

• 1)    породный массив имеет изотропные и однородные теплофизические свойства в зонах льда и охлаждения;

• 2)    фазовый переход поровой воды происходит полностью в некотором малом заданном интервале температур;

• 3)    вертикальная составляющая тепловых потоков пренебрежимо мала по сравнению с горизонтальной;

• 4)    в начальный момент времени массив полностью водонасыщен;

• 5)    вода в поровом пространстве массива считается неподвижной;

• 6)    локальное тепловое равновесие между твердыми частицами породы, водой и льдом в каждом элементарном объеме обводненного породного массива;

• 7)    центры устьев замораживающих колонок расположены на окружности, а сами колонки ориентированы строго вертикально и удалены друг от друга на одинаковое расстояние.

Третье допущение позволяет перейти от трехмерной задачи к двумерной. Однако данное допущение требует дополнительных комментариев. Оно применимо только в случае, если рассматривать срединное сечение горизонтального слоя пород достаточно большой мощности (более 10 м), а временной интервал моделирования при этом также ограничивать (менее 200 сут). В этом случае влияние вертикальных тепловых потоков будет иметь место изначально только на границах рассматриваемого слоя пород с соседними верхним и нижним слоями. С течением времени это влияние будет распространяться вглубь слоя пород и в определенный момент, достигнув его срединного горизонтального сечения, будет приводить к существенному искажению поля температур по сравнению с чисто двумерным случаем – начиная с этого момента времени третье допущение применять нельзя.

2021;6(3):192–202

Введенные допущения 1, 3, 5 и 7 позволяют сделать заключение о наличии вращательной симметрии в задаче. Это существенно упрощает геометрическую модель и позволяет не рассматривать горизонтальный разрез породного массива целиком, а рассмотреть его отдельный сектор, ограниченный двумя главными плоскостями ЛПО [5]. Геометрическая модель сектора замораживаемого породного массива представлена на рис. 1. Данная модель использовалась далее для проведения численных расчетов.

В геометрической модели слоя породного массива присутствует несколько границ – S , V , B и I . Граница I представляет собой внутреннюю границу расчетной области. Она «отсекает» и убирает из рассмотрения малый объем породного массива вблизи начала координат (центра контура замораживания). Она введена для того, чтобы не строить конечно-элементную сетку около острого угла, касающегося оси вращательной симметрии расчетной области. Это позволяет улучшить качество элементов сетки и повысить устойчивость численного решения. Границу I следует как можно сильнее смещать к оси вращательной симметрии области, чтобы «отсекаемый» объем массива был пренебрежимо мал по сравнению с общим объемом массива, подверженного тепловому воздействию.

V ce ( T ) H

1,

T < T„ sd

( T lq - T )/( T q - T sd ), T sd <  T <  T q ,

0,

T < t lq

где H ₀ – референтная удельная энтальпия пород при температуре I_sd , Дж/м³; c_lq , c_sd – удельные теплоемкости породного массива в зонах охлаждения и льда соответственно, Дж/(кг · °C); ρ _lq , ρ _sd – плотности породного массива в зонах охлаждения и льда соответственно, кг/м³; T_lq – температура начала кристаллизации поровой воды (или температура ликвидуса), °С; T_sd – температура начала плавления порового льда (или температура солидуса), °С; L – удельная теплота кристаллизации поровой воды, Дж/кг; n – пористость массива; ρ _w – плотность воды, кг/м³.

Помимо этого, модель (1)–(4) дополняется гра-

ничными и начальными условиями:

^t ^ -a( T b ( t ) - T ) d N

— 0,

B

T v = T o ,                     (6)

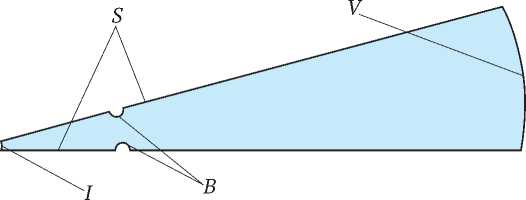
Рис. 1. Расчетная область и ее границы:

S – симметрия; B – стенки замораживающих колонок;

V – внешняя граница, соответствующая непотревоженному породному массиву; I – внутренняя граница

d T dNS

— 0,

Математическая модель породного массива, подверженного тепловому влиянию замораживаемых колонок, основана на уравнении баланса энергии в энтальпийной форме [18, 19]:

dh(t) Г d <„ dt) d f, dt) — л +л d t    [dx ( dx ) dy ( dy )

^{Л —Л} Iq ⁽¹ -^ cce ) ^{+ Л} sd ^ ice ,

где H – удельная энтальпия пород, Дж/м³; x , y – декартовы координаты, м; t – время, с; λ _lq , λ _sd – теплопроводности породного массива в зонах охлаждения и льда соответственно, Вт/(м · °C); λ _ice – льдистость пород, м³/м³.

Уравнение баланса энергии дополняется уравнениями состояния:

P Iq C lq ( T - T q ) + P w nL ,     T q <  T

H ( T ) — H 0 + ^

P w^nL • ⁽1 -V ice ), .P sd C _sd ( T - T_sd ),

T . <  T <  T , sd              lq ,

T < T, sd

d T

IN, - °’ <⁸⁾

^T\_t — 0 — ^T 0 , (9)

где T_fb ( t ) – температура рассола в замораживающих колонках, °С; T ₀ – температура непотревоженного породного массива на удалении от контура замораживания, °С; α – коэффициент теплоотдачи от массива к рассолу через стенку замораживающей колонки, Вт/(м² · °С); N – координата вдоль нормали к рассматриваемой границе расчетной области, м.

Фазовый переход воды из жидкого в твердое состояния и обратно учитывается в модели посредством задания нелинейной функции (3) удельной энтальпии H от температуры Т . В коротком интервале температур [ T_sd , T_lq ] данная функция резко возрастает на величину, равную скрытой теплоте фазового перехода ρ _wnL в единице объема обводненного породного массива. Такой подход к учету фазового перехода называется энтальпийным и находит широкое применение в задачах с фазовыми превращениями в твердых телах [16, 18].

Как и ранее [5, 10], аварийный режим работы системы замораживания связан с отключением (выхода из строя) одной из замораживающих колонок в момент перехода на пассивный режим замораживания. Отключение замораживающей колонки моделируется посредством задания нулевого коэффициента теплоотдачи на временном промежутке, начиная с момента перехода на пассивный режим замораживания.

По мнению авторов, пассивный режим замораживания наиболее опасен с точки зрения возникновения неисправностей и аварий. Это связано с тем,

2021;6(3):192–202

что, во-первых, в начале пассивного режима замораживания происходит изменение режима работы замораживающей станции, что само по себе повышает риск выхода из строя отдельных элементов системы замораживания. Во-вторых, проходка и крепление шахтного ствола осуществляются именно на стадии пассивного замораживания. В практике строительства шахтных стволов многократно возникали случаи, когда замораживающие колонки выходили из строя по причине сильного деформирования породы до возведения передовой бетонной крепи [2, 20, 21]. Помимо этого, отключение части замораживающих колонок является одним из возможных мероприятий по снижению количества отбираемой теплоты из породного массива на стадии пассивного замораживания [14, 22].

Также в конце стадии активного замораживания на строящихся стволах часто проводятся дополнительные измерительные процедуры, направленные на проверку достижения сплошного ЛПО заданной толщины [23, 24]. Эти измерения могут проводиться как в контрольных, так и в замораживающих скважинах (например, ультразвуковой контроль или термометрические измерения). Это также повышает риск повреждения замораживающих колонок.

Методика численного моделирования

Численное решение задачи (1)–(9) искалось с помощью метода конечных элементов в программном комплексе ANSYS (модуль Thermal Transient). Реше- ние строилось на сетке, состоящей из прямоугольных элементов (см. рис. 2, а). Размер элементов сетки в расчетной области и параметры сгущения сетки вблизи замораживающих колонок подбирались на основании предварительного моделирования таким образом, чтобы обеспечить независимость решения от способа дискретизации.

В качестве параметров для проведения численных расчетов взяты исходные данные для проекта по замораживанию пород для условий строящихся стволов одного калийного рудника в республике Беларусь. Исследовался слой глины как один из наиболее теплопроводных слоев в интервале замораживаемых пород. Основные теплофизические свойства рассматриваемого слоя пород представлены в табл. 1. Плотность пород в зоне льда принималась равной плотности пород в зоне охлаждения. Представленные в таблице теплопроводности в зонах льда и охлаждения являются нетипичными для рассматриваемого слоя глины. Это связано с несколькими факторами: наличие в глине прослоев песка, высокое давление в естественном залегании (около 1 МПа), низкая пористость. Помимо этого, следует отметить, что указанные в табл. 1 теплопроводности и влажность пород были немного (в пределах 15 %) скорректированы по сравнению со своими начальными значениями в процессе настройки теплофизической модели по данным измерений температуры в контрольно-термических скважинах на строящемся объекте.

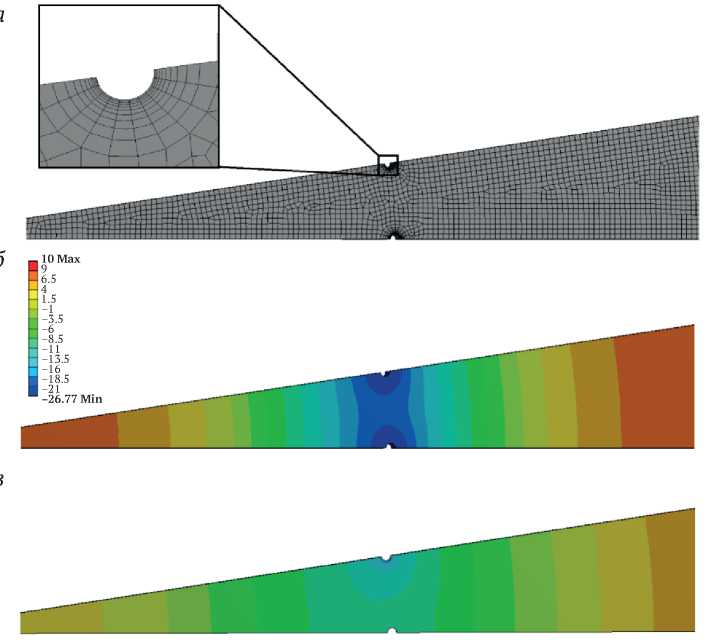
Рис. 2. Конечно-элементная модель слоя породного массива ( а ), рассчитанное распределение температуры в нем на стадии активного замораживания ( б ) и на стадии пассивного замораживания при аварийном отключении одной из колонок ( в )

2021;6(3):192–202

Таблица 1

Теплофизические свойства слоя глины

Свойство	Значение
Теплопроводность (зона льда), Вт/(м · °С)	4,30
Теплопроводность (зона охлаждения), Вт/(м · °С)	2,64
Теплоемкость (зона льда), Дж/(кг · °С)	900
Теплоемкость (зона охлаждения), Дж/(кг · °С)	1712
Начальная температура пород, °С	10
Температура ликвидуса, °С	–0,4
Температура солидуса, °С	–0,9
Плотность, кг/м3	1840
Пористость, доли единицы	0,158

На стадии активного замораживания по колонкам движется замораживающий рассол с постоянной температурой, равной –30,4 °С. При переходе на стадию пассивного замораживания, температура рассола в течение 5 сут равномерно поднимается до величины –20 °С. Расход замораживающего рассола на стадиях активного и пассивного замораживания постоянен и равен 240 м³/ч. Коэффициент теплоотдачи, рассчитанный по методике, приведенной в [5], равен 62,5 Вт/(м² · °С). Внешние границы ЛПО определялись по изотерме T_d = –8 °С, при которой рассчитывалась проектная толщина ЛПО по условиям прочности и ползучести.

Радиус внешней границы расчетной области равен 40 м, а радиус внутренней границы (отсекаемой зоны) – 0,25 м. Контур замораживающих колонок имеет радиус 8 м. Замораживающие колонки имеют внешний диаметр 0,146 м и внутренний диаметр 0,136 м. Расстояние между центрами соседних замораживающих колонок принято равным около 1,2 м (случай 42 замораживающих колонок, удаленных друг от друга на одинаковое расстояние).

На рис. 2, б представлено рассчитанное распределение температуры в рассматриваемом секторе для момента времени 50 сут (стадия активного замораживания). Наименьшее значение толщины ЛПО на стадии активного замораживания наблюдается вдоль замковой плоскости ЛПО, в то время как на стадии пассивного при аварийном отключении одной из замораживающих колонок (см. рис, 2, в , момент времени 100 сут) – вдоль главной плоскости ЛПО. По этой причине в качестве толщины ЛПО бралось минимальное из двух значений толщин, рассчитанных вдоль главной и замковой плоскостей ЛПО.

Влияние времени активного замораживания на состояние ЛПО

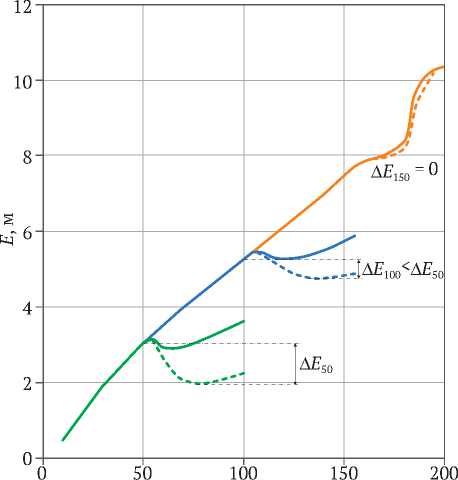
Рассчитаны временные зависимости толщины ЛПО для нескольких различных вариантов перехода на пассивное замораживание: спустя 50, 100 и 150 сут (рис. 3). Штриховой линией представлены кривые, соответствующие аварийному отключению одной из замораживающих колонок, а сплошной линией – безаварийному переходу на стадию пассивного замораживания.

Анализируя рис. 3, можно заключить, что при переходе на пассивное замораживание как в аварийном, так и в безаварийном режиме происходит кратковременное уменьшение толщины ЛПО. Об этом свидетельствуют характерные «ямы» на кривых динамики толщины ЛПО. Они особенно характерны для случая, когда длительность стадии активного замораживания минимальна и составляет 50 сут. По мере увеличения длительности активного замораживания глубина этих «ям» уменьшается и в конечном счете, начиная с некоторого момента времени, уменьшение толщины ЛПО на стадии пассивного замораживания прекращается. В рассматриваемом случае этот момент времени находится между 100 и 150 сут.

t , суток

150 суток нормальный режим

100 суток нормальный режим

50 суток нормальный режим

150 суток аварийный режим

100 суток аварийный режим 50 суток аварийный режим

Рис. 3. Динамика толщины ЛПО Е при переходе на пассивное замораживание

Оценить глубину «ям» на кривых временной динамики ЛПО на рис. 3 можно, введя следующий количественный критерий – максимальное уменьшение толщины ЛПО ∆ E [5]:

^ E = max(0; E_a - E n ),           (10)

где E_П – проектная (минимально-допустимая) толщина ЛПО, которая была достигнута на конец стадии активного замораживания, м; E_a – минимальная толщина на стадии пассивного замораживания, м.

В работе [5] произведен подробный количественный анализ данного критерия для двух слоев пород – глины и мела. В результате получено, что при небольших длительностях активного замораживания массива (менее 100 сут) уменьшение толщины ЛПО ∆ E существенно нелинейно зависит от длительности активного замораживания, что связано с особенностями теплопереноса вблизи внутреннего и внешнего фронтов ЛПО.

2021;6(3):192–202

В настоящей работе мы сосредоточим внимание на другом интересном факте о критерии (10). При больших длительностях активного замораживания массива (более 100 сут) величина ∆ E уменьшается с ростом длительности стадии активного замораживания пород и в конечном счете обращается в нуль – как для случая безаварийной работы системы замораживания, так и в аварийном случае при поломке одной из замораживающих колонок. Физически данный вывод закономерен с учетом того, что чем дольше длится стадия активного замораживания, тем глубже успевает охладиться и замерзнуть породный массив и, следовательно, тем выше «инерционность» тепловых потоков в нем. Под инерционностью в данном случае понимается способность замороженного породного массива сохранять отрицательные температуры длительное время после того, как холодильная мощность замораживающей станции была снижена.

С учетом данного вывода целесообразным является выбор длительности активного замораживания пород исходя из условия ∆ E = 0. Данное условие, по сути, означает, что на стадии пассивного замораживания толщина ЛПО не должна уменьшаться до величин ниже проектных. Для рассматриваемого слоя пород минимальная длительность стадии активного замораживания пород, при которой выполняется ∆ E = 0, составляет около 130 сут или примерно 4,3 мес.

Влияние расстояния между колонками на формирование ЛПО

Представляет интерес исследование зависимости критерия ∆ E от расстояния между двумя соседними замораживающими колонками. В настоящей работе проведен такой анализ для слоя глины. На рис. 4 представлены полученные в результате численного моделирования зависимости критерия ∆ E от расстояния а между соседними замораживающими колонками длительностей активного замораживания 50, 100, 120, 130 и 150 сут и для ситуации аварийного отключения одной из замораживающих колонок. Рассмотрены пять различных расстояний между замораживающими колонками: 0,72, 0,96, 1,2, 1,44 и 1,68 м. Анализ расстояний между замораживающими колонками 0,7 м и меньше не имеет смысла вследствие сложности или невозможности реализации таких расстояний на практике с учетом закладываемых по проекту отклонений положений замораживающих колонок от вертикали.

Из рис. 4 следует вполне закономерный факт: критерий ∆ E является монотонно возрастающей функцией расстояния между соседними замораживающими колонками. Чем больше время активного замораживания, тем сильнее успевает охладиться и заморозиться породный массив и тем меньше значение критерия (10) и меньше отрицательный эффект от внезапного выхода из строя замораживающей колонки. В целом функциональный вид критерия ∆ E ( a ) существенно нелинейный.

Для 50 сут активного замораживания при всех рассмотренных расстояниях между замораживающими колонками наблюдались ненулевые уменьшения толщины ЛПО. При этом для 150 сут активного замо- раживания критерий (10) обратился в нуль для всех рассмотренных расстояний, кроме 1,68 м. Для наиболее распространенных на практике расстояний между замораживающими колонками (от 1,1 до 1,3 м) толщина ЛПО будет уменьшаться, если время активного замораживания составляет менее 130 сут.

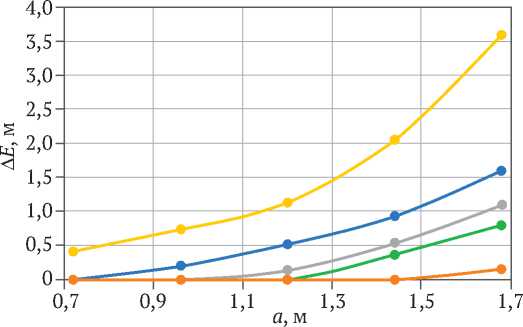
-е- 50 суток -•- 100 суток    —•-120 суток

-•-130 суток    -•-150 суток

Рис. 4. Максимальное уменьшение толщины ЛПО как функция расстояния между двумя соседними замораживающими колонками

Как отмечалось в работе [5], толщина ЛПО по изотерме фактического замерзания воды (около 0 °С) не уменьшается и сохраняет положительную скорость роста на протяжении всего периода пассивного замораживания, независимо от длительности активного замораживания. При этом, как видно из полученных здесь расчетов, уменьшение толщины ЛПО по изотерме –8 °С существенно, а значит существенно и снижение средней температуры ЛПО, если последнее считается по изотерме фактического замерзания воды. Это указывает на мнимую надежность ЛПО, толщина которого определена по изотерме фактического замерзания воды.

Безопасное расстояние а между замораживающими колонками, при котором не произойдет существенного уменьшения толщины ЛПО, зависит от проектного времени активного замораживания породного массива. Большее время активного замораживания является более предпочтительным, т. к. в этом случае удается снизить уменьшение толщины ЛПО, вызванное переходом на пассивный режим замораживания и выходом из строя одной из замораживающих колонок. Если принять в качестве критерия безопасности при выборе расстояния а условие ∆ E = 0 м, то для 100 сут активного замораживания величина а составляет примерно 0,7 м, в то время как для 150 сут активного замораживания – уже около 1,5 м. С учетом того, что на практике расстояния между соседними замораживающими колонками обычно находятся в интервале от 1,1 до 1,3 м, достаточно потребовать, чтобы время активного замораживания породного массива составляло не менее 130 сут (около 4,3 мес). Полученное безопасное время активного замораживания справедливо только для рассмотренного слоя глины.

2021;6(3):192–202

При больших значениях расстояния а время активного замораживания следует выбирать на основании рис. 4 или аналогичных количественных оценок с использованием критерия (10) или подобных ему критериев. Естественно, выбор времени активного замораживания пород должен основываться также на ряде других критериев, например, минимальном времени замораживания пород до проектных толщин. Данный критерий совместно с предложенным критерием по ∆ E позволит определить оптимальный режим работы замораживающей станции на стадиях активного и пассивного замораживания.

Важно отметить, что полученные в статье результаты соответствуют случаю достаточно резкого увеличения температуры рассола при переходе на пассивное замораживание и дальнейшему поддержанию данного значения с течением времени на протяжении всей стадии пассивного замораживания. Существует также и альтернативный подход к обеспечению заданной толщины ЛПО на стадии пассивного замораживания, связанный с плавным изменением температуры (и при необходимости расхода) рассола на длительном временном интервале. Однако этот альтернативный подход оказывается не всегда применим из-за ограниченных технических возможностей: зачастую применяемое при строительстве стволов холодильное оборудование не позволяет осуществлять гибкое управление холодильной мощностью [25].

Заключение

Проведено теоретическое исследование изменения толщины ледопородного ограждения (ЛПО) на стадии пассивного замораживания в нормальном и аварийном режимах работы замораживающей станции. В качестве примера рассмотрен слой глины из интервала замораживаемых пород для строившихся стволов одного калийного рудника в республике Беларусь. Ниже приведены основные результаты, полученные в работе:

• 1.    При выборе длительности стадии активного замораживания пород необходимо учитывать условие поддержания проектной толщины ЛПО на стадии пассивного замораживания. Выполнение этого условия сильно зависит от того, насколько породный массив успел охладиться вглубь. Для рассматриваемого слоя глины получено, что минимальная длительность стадии активного замораживания пород, обеспечивающая проектную толщину ЛПО при пассивном замораживании, составляет примерно 4,3 мес.

• 2.    При анализе изменения толщины ЛПО при различных расстояниях между замораживающими колонками получено, что для наиболее распространенных расстояний между колонками в интервале от 1,1 до 1,3 м требуется соблюдать ограничения по длительности активного замораживания для предотвращения критического уменьшения толщины ЛПО на стадии пассивного замораживания либо уменьшать расстояние между замораживающими колонками. В этом случае будет обеспечено сохранение положительной динамики роста толщины ЛПО. Для рассмотренного в работе слоя глины и расстояний между колонками от 1,1 до 1,3 м минимальное время активного замораживания также составляет около 4,3 мес.

Представленные выше выводы важны ввиду имеющегося в настоящее время тренда на уменьшение времени активного замораживания пород с целью ускорения строительства шахтных стволов. Так, например, для условий строящихся стволов нескольких калийных рудников в России и Беларуси проектное время активного замораживания составляет от 3 до 4 мес. Здесь следует помнить, что снижение времени активного замораживания может оказаться небезопасным из-за потенциального снижения толщины ЛПО и потери его сплошности при переходе на пассивное замораживание при возможном выходе из строя одной или нескольких замораживающих колонок.

2021;6(3):192–202

2021;6(3):192–202

2021;6(3):192–202