Определение токов утечки при отсутствии контакта человека с грунтом
Автор: Калинина Алиса Сергеевна, Непопалов Валерий Николаевич, Сидоров Александр Иванович
Журнал: Вестник Южно-Уральского государственного университета. Серия: Энергетика @vestnik-susu-power
Рубрика: Электроэнергетика
Статья в выпуске: 11 (111), 2008 года.
Бесплатный доступ
В статье получены аналитические зависимости емкости цилиндрической фигуры относительно земли и заземленной проводящей поверхности. На основании полученных зависимостей показан характер распределения полного тока утечки при емкостной связи цилиндрической поверхности с землей и заземленной металлоконструкцией.
Короткий адрес: https://sciup.org/147158038
IDR: 147158038 | УДК: 658.382
Текст научной статьи Определение токов утечки при отсутствии контакта человека с грунтом
В соответствии с формулами, полученными в [1], вычислим значения тока утечки (рис. 1), протекающего через тело человека, находящегося под трехфазной линией электропередачи на расстоянии х от проекции средней фазы, при условии гальванической связи человека с землей и в удалении от металлоконструкций.
В производственных условиях подобная ситуация практически невозможна. Персонал, занятый обслуживанием ЭУ СВН, обут в специальную обувь и имеет емкостную связь с землей. Кроме того, изменение величины тока, протекающего через тело человека по сравнению с «идеализированной ситуацией» происходит за счет наличия на территории ОРУ заземленных металлоконструкций, в результате чего появляются емкостные связи человек-металлоконструкция. Вследствие этого, при расчете тока утечки необходимо учитывать емкостную связь человека, как с землей, так и с металлоконструкциями.
Поскольку расчет емкости тела человека относительно земли и относительно заземленной металлоконструкции вызывает определенные трудности, ток, протекающий через тело человека, определяется площадью его поверхности, тело человека заменим цилиндром высотой I = 1,8 м и радиусом го = 0,25 м, а заземленную металлоконструкцию - однородной проводящей поверхностью.
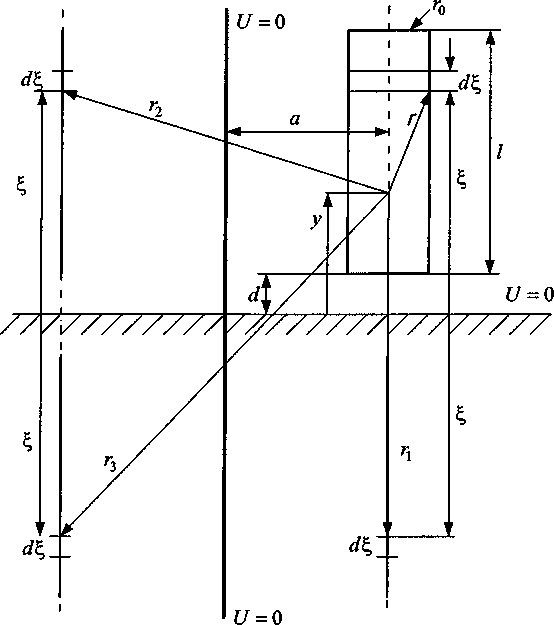
Определим емкость боковой поверхности указанного цилиндра, относительно плоскости земли. Фигура расположена на расстоянии d от земли (рис. 2).
Для расчета емкости сложных систем широко используется приближенный метод, предложенный Хоу [2].
Введем отображение цилиндрической поверхности в плоскости земли. При вычислении потенциала примем, что заряды отображенной поверхности распределены с одинаковой линейной плотностью на её оси.
Потенциал в точке у на оси фигуры I от заряда q — dq равен:
du — у 4ле0/г
Потенциал в той же точке у от заряда на элементе d^ зеркального отображения равен:
у2 4ns0Z/i
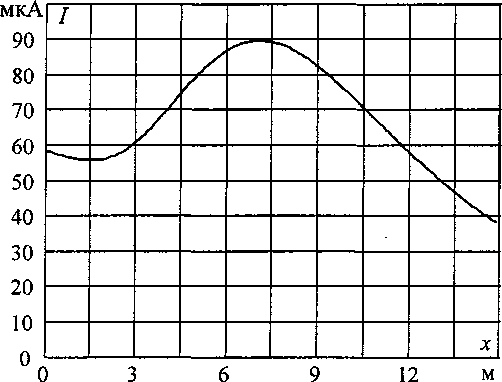
Рис. 1. Зависимость тока утечки на землю через тело человека, находящегося под трехфазной линией электропередачи
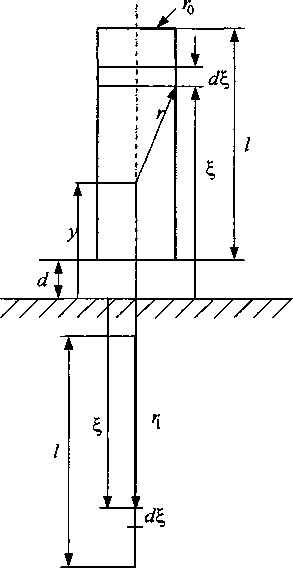
Рис. 2. Расчетная схема для вычисления емкости цилиндрической фигуры относительно земли
Полный элементарный потенциал в рассматриваемой точке равен:
Находим
dUy
q
4та01
1 1
Отсюда получаем
d+W
+< f 1 11
J ---^. dV ri)
d y 4ле0/
Расстояния
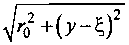
Обозначим:
и ri соответственно равны
d+i dE
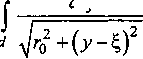
d1 dE
d
В интеграле Л делаем замену г = у - £ , следовательно dz = -dE,, z = у-d ; ^ = d + l, z = y-d-l.
переменной: при ^ = d,
Находим y-d-l
у-d
-dz 2 2
n + Z
= Arsh —
= Arsh [ -—-I r0
-Arsh
W V y-d-l y-d-lA
r0
В интеграле Л делаем замену переменной z = у + ^ , следовательно dz = dE,, при ^ = d, z = y + d; ^ = d + 1, z = у + d + l.
dz y + d + l л z У + d y+d z
Подставляя (5), (6) в формулу (4) получаем потенциал
y 4ле0/
-Arsh
Arsh
y-d
y-d-l
г0
y + d + l
— In—------ y + d
Среднее значение потенциала определяется по формуле:
. d*l
1 d
q 4ks0Z2
l+d '
- J Arsh
l+d f
- J Arsh d V
Интеграл
l+d (
J Arsh d < тогда ' l+d (
y-d-l
У-d r0
• J Arsh
г0
d V l+d
d
dy= - J Arsh
У-d г0
l+d Г
= 2 | Arsh d I
d
У-d r0
^» .(8) y + d
y-d-l
l+d Г dy - J Arsh d <
У-d r0
г0
dy, (9)
y-d-l
r0
Электроэнергетика
Следовательно
U = —-—
СР 4ле0/2
l+d
d
Интеграл l+d Г
2 j Arsh d I
y + d + l y + d
(И)
у-d 'о
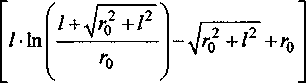
не зависит от d. Интеграл
l+d
JIn
d
у 4- d +1 y + d
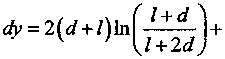
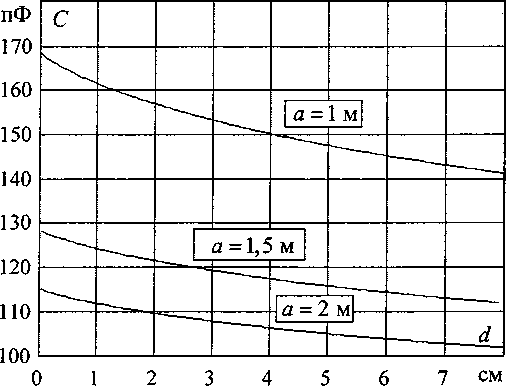
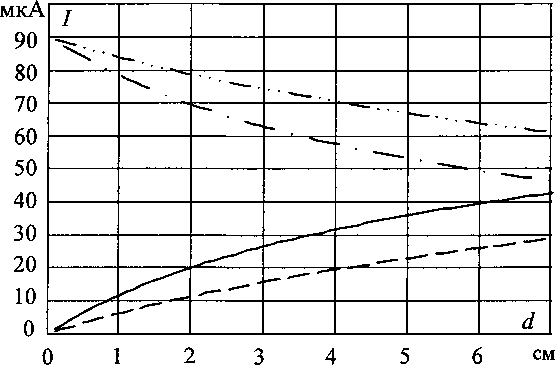
+2ь(у~у+ 2(2 Для упрощения обозначим: (j Г Z+tZ ] d ( «12 - 2 , (15) Емкость боковой поверхности цилиндрической фигуры относительно плоскости земли определяется по выражению C^d^q^, (17) следовательно «п — а12 Подставляя в формулу (18) с учетом (14) и (15) длину Z цилиндрической поверхности, равной высоте роста среднего человека h = 1,8 м и радиусом г0 = 0,25 м, получаем зависимость C^d^ (рис. 3). В данном случае расстояние до земли d Ф 0. Чтобы учесть возникающую емкостную связь с металлоконструкцией, определяем емкость боковой поверхности цилиндрической фигуры длиной Z, радиусом г0, относительно плоскости земли. Как и в первом случае, цилиндрическая фигура расположена на расстоянии d от земли, но на расстоянии а от оси фигуры расположена заземленная проводящая поверхность (рис. 4). Полагается также, что суммарный заряд q распределен по длине фигуры Z равномерно. Введем отображения цилиндрической поверхности. При вычислении потенциала примем, что заряды отображающих поверхностей распределены с одинаковой линейной плотностью на их осях. Потенциал в точке у на оси фигуры Z от заряда "dt, равен: dUyU"4TOoIr Потенциалы в той же точке у от заряда у dl, получим ^ср = («11-“12)^-- (16) ZTCEq зеркальных отображений соответственно равны: “^12 ~ ' 4ле0‘,1 Рис. 3. Зависимость емкости боковой поверхности цилиндра относительно земли от расстояния до земли d Рис. 4. Расчетная схема для вычисления емкости цилиндрической фигуры относительно земли с учетом заземленной проводящей поверхности ятт qd^ ■ dU =--: у 4Л£0/г2 у3 4ле0/г3 Расстояния г, гь г2 и г3 соответственно равны Полный элементарный потенциал в рассматриваемой точке равен: dU=-^- у 4ле0/^г Отсюда получаем d+lf . и =-9— J -4ле0/ Иг г2 г3; Среднее значение потенциала определяется по формуле . d*i UC¥=-^Uydy=- \ (UyX-Uy2+Uy3^. (25) 1 d Вклад в среднее значение от потенциала UyX определенный по формуле (7): . d+l ^ср. =7 J ^1^ = [“И -«12 (^)]^- ■ / d2Л8 Интеграл d+l Г з d+l1 J2 = J - ^ = J . э э d^, (27) 1 1 1 Lr ---+— d^ = rl r2 r3 J после замены 2а на г0 приводим к интегралу Jx, следовательно z q 4ле0/ d+u i > — f1 4ле0/ Дг2; d+lf • T4 1 1 ( 1-1 ^- dV м d+l f q r 4ле07 j = иуХ - иу2 +иу3, где UyX- вклад в среднее значение от dUyU и ^>12 • ^ • (28) 2а ) ср2 4Л8О7 d Электроэнергетика d+/ Для упрощения обозначим а13=2^-------у----------, (30) q 4ле072 Z-ln 2 получим =(31) ZTISq В интеграле dту d+/»у г d^ гdL J3 = I — = I —,===?= делаем за мену переменной z = у + E. Теперь dz = d^, при E, = d, z = y + d; E, = d+ I, z=y + d +1, следовательно Z + V l + ^af+l2 Для упрощения обозначим найдем ^-q. 2ле0 , , (y + d + lA , . fy + dA = Arsh ------- - Arsh ----- . (32) v 2a ) I 2ti J Среднее значение потенциала Емкость боковой поверхности цилиндрической фигуры относительно плоскости земли с учетом влияния проводящей поверхности равна d+i q 2ле0/2 -^a2*^*!)2 -(2d+ 7) Arsh [ ^^ +J4^+(2J + /7+ v Va) Учитывая, что расстояние до земли много меньше расстояния до проводящей поверхности d « а, после преобразований получим “11 -“12 "“13 + “14 По формуле (37) с учетом (14), (15), (30) и (35) вычислим зависимости емкости боковой поверхности цилиндрической фигуры C^d^ длиной Z = 1,8 м, радиусом г0= 0,25 м, относительно плоскости земли (рис. 5), задавая расстояния до заземленной проводящей поверхности равными а = 1 м, 1,5 м и 2 м соответственно. На рис. 1 максимальное значение тока, протекающего через тело человека, находящегося под трехфазной линией электропередачи, составляет 90 мкА. На примере данной величины тока утечки вычислим составляющие величины тока при наличии емкостной связи цилиндрической Рис. 5. Зависимости емкости боковой поверхности цилиндра относительно земли от расстояния до земли d для различных расстояний до проводящей поверхности а Рис. 6. Величина тока утечки при емкостной связи цилиндрической поверхности относительно земли и заземленной металлоконструкции от расстояния d — .. — составляющая тока утечки, протекающего через дно цилиндра с учетом при отсутствии заземленной металлоконструкции; —---составляющая тока утечки, протекающего через дно цилиндра с учетом заземленной металлоконструкции; составляющая тока утечки, протекающего через боковую поверхность цилиндра с учетом заземленной металлоконструкции; ____составляющая тока утечки, протекающего через боковую поверхность цилиндра при отсутствии заземленной металлоконструкции поверхности с землей и заземленной металлоконструкцией (рис. 6). Принимая, что полное значение емкостного тока утечки остается неизменным [3]. Выводы 1. Получены формулы для расчета тока утечки через тело человека при наличии и отсутствии гальванической связи между телом человека и землей. 2. На основании полученных формул проведены расчеты для разных условий контакта с грунтом. Сопоставление полученных данных с результатами экспериментальных исследований показывают хорошую сходимость.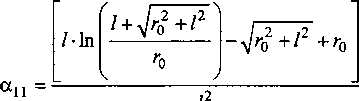
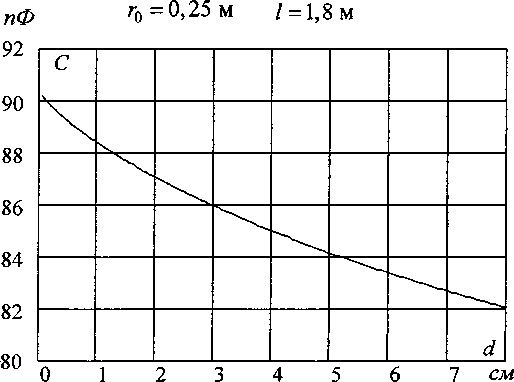
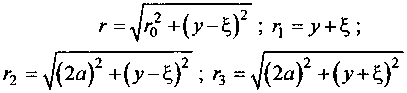
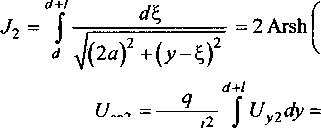
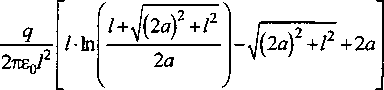
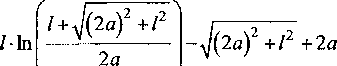
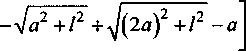
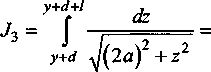
Список литературы Определение токов утечки при отсутствии контакта человека с грунтом
- Калинина А.С. Аналитическое исследование плотности тока электрического смещения и распределения напряженности электрического поля под линией электропередач/А.С. Калинина, В.Н. Непопалов, А.И. Сидоров//Электробезопасность. 2005. № 3-4. С. 60-67.
- Нейман Л.Р. Теоретические основы электротехники/Л.Р. Нейман, К.С. Демирчян, Н.В. Коровкин, В.Л. Чечурин. СПб.: Питер, 2003. 462 с.
- Долин П.А. Основы техники безопасности в электроустановках/П.А. Долин. М.: Энергия, 1979. С. 306-320.