Определение уровня заряда литий-ионного аккумулятора на основе алгоритма расширенного фильтра Калмана
Автор: Сяоган У, Ли Сюефэн, Щуров Н.И., Штанг А.А., Ярославцев М.В., Дедов С.И.
Журнал: Журнал Сибирского федерального университета. Серия: Техника и технологии @technologies-sfu
Статья в выпуске: 4 т.13, 2020 года.
Бесплатный доступ
При определении уровня заряда (УЗ) накопителя энергии электрического транспортного средства (ЭТС) на основе схемы замещения литий-ионного аккумулятора (ЛИА) возникают значительные трудности. Так, для оценки УЗ использован расширенный фильтр Калмана (EKF, Extended Kalman filter). Моделирование и экспериментальные результаты показывают, что оценка УЗ может быть выполнена с использованием алгоритма EKF для дорожных условий по циклу движения в Китае (Chinacar) и новому европейскому циклу (NEDC). По сравнению с кулонометрическим методом средняя ошибка оценки УЗ - 1,042 и 1,138 % для циклов соответственно, максимальная ошибка не превышает 4 %. Применение алгоритма для определения УЗ имеет достаточную устойчивость и сходимость.
Литий-ионный аккумулятор, электротранспорт, оценка уровня заряда, фильтр калмана, дорожные условия
Короткий адрес: https://sciup.org/146281629
IDR: 146281629 | УДК: 621.355 | DOI: 10.17516/1999-494X-0242
Текст научной статьи Определение уровня заряда литий-ионного аккумулятора на основе алгоритма расширенного фильтра Калмана
ЛИА, являясь одним из основных узлов электромобиля, предполагает использование совместно с методами эффективного управления с целью продления срока службы, а также повышения надежности и безопасности. Точная оценка УЗ батареи позволяет предотвратить перезаряд и разряд сверх рабочего диапазона, уменьшить возможные повреждения и повысить производительность [1].
В научных работах определение УЗ батареи в основном сосредоточено на построении модели батареи и разработки алгоритма. В работе А.В. Борисевича [2] дан краткий обзор двух основных классов моделей ЛИА для систем управления батареями: эмпирических и физических. А.А. Андреев [3] провел моделирование работы литий-железофосфатного аккумулятора в условиях работы при низких температурах. В предложенной модели батареи Hongwen He и др. [4] обобщили различные эквивалентные схемы, в том числе модели Rint, Тевенина, RC, PNGV и DP, а также провели сравнение и анализ пяти эквивалентных схем замещения. Rui Xiong [5] использовал модель электрохимической поляризации Нернста для определения параметров и оценки УЗ батареи, используемой в подзаряжаемых гибридных транспортных средствах. Wei He [6] предложена модель нейронной сети для определения УЗ батареи, а Yong Tian [7] – мо- дифицированной эквивалентной схемы замещения, которая увеличивает точность расчета и снижает расход заряда батареи.
В.В. Печенко [8] привел описание модели с единственным состоянием поведения ячейки аккумуляторной батареи, которая рассмотрена как нелинейная динамическая система, представленная в форме дискретных по времени состояний. В работе Л.А. Скрипко [9] рассмотрены проблемы определения степени износа литий-ионного аккумулятора в процессе эксплуатации электромобиля или гибридного автомобиля. Cheng Lin [10] и Yongzhi Zhang [11] получили модель эквивалентной RC-схемы третьего порядка и модель ЛИА на основе гауссовой функции, однако обе модели являются относительно сложными, как и осуществление расчета по ним. В исследовании Li [12] используется метод определения УЗ с начальной коррекцией кулонометрическим методом для устранения накапливающейся ошибки. Michael A. Roscher [13] использовал метод измерения напряжения разомкнутой цепи для оценки УЗ, и в конечном итоге ошибка оценки составила не более 2 %. Hongwen He [14] выполнил мониторинг УЗ батареи в реальном времени с использованием алгоритма сигма-точечного фильтра Калмана (UKF) и адаптивного расширенного фильтра Калмана (AEKF). Кроме того, для оценки заряда УЗ используют алгоритмы интеллектуального анализа. Так, A. Zenati [15] применил алгоритм нечеткой логики для оценки УЗ ЛИА.
Таким образом, оценка УЗ в основном сосредоточена на применении кулонометрического метода, измерения напряжения разомкнутой цепи, алгоритмов фильтра Калмана, а также интеллектуальных алгоритмов. Однако кулонометрический метод является прямым методом измерения УЗ, который требует начального значения и высокоточного измерения тока, также возникает проблема накопления ошибки [16]. Метод измерения напряжения разомкнутой цепи достаточно длителен и не применим к оценке УЗ в реальном времени [17]. Алгоритмы интеллектуального анализа требуют предварительного сбора статистического материала, что ограничивает их широкое применение [18]. Метод фильтра Калмана применялся в оценке УЗ систем управления батареями, однако традиционный фильтр Калмана не применим к нелинейным системам. Для нелинейной модели батареи этап линеаризации можно добавить при выводе уравнения фильтрации, что может быть эффективным решением применения фильтра Калмана в нелинейных системах [19]. В работе для оценки УЗ батареи используется расширенный алгоритм фильтра Калмана (EKF), а определение параметров и УЗ батареи при работе выполняется согласно циклам Chinacar и NEDC. Затем для проверки эффективности алгоритма результаты сравнивали с данными, полученными кулонометрическим методом.
Модель аккумулятора и определение его параметров
Создание эквивалентной схемы. В настоящее время модели аккумуляторов, используемые для оценки УЗ, в основном делятся на три типа: электрохимические модели, модели нейронной сети и эквивалентные схемы. Эквивалентная схема включает в себя сопротивления, емкости, источник постоянного напряжения и другие компоненты, которые могут имитировать динамические характеристики батареи. По сравнению с электрохимической моделью и моделью нейронной сети преимущество эквивалентной схемы в простоте математического описания, легкости идентифицируемых параметров модели и возможности определения любого УЗ батареи [20]. Эквивалентные схемы разделяют на модель Rint, Тевенина, PNGV и GNL. Модель – 422 –
Тевенина является эквивалентной схемой полимерной ЛИА, имеющей умеренную сложность расчета и высокую точность. В статье в качестве эквивалентной схемы выбрана модель Теве-нина [21, 22]. Эквивалентная схема показана на рис. 1, где UOC представляет собой напряжение разомкнутой цепи батареи ( V ), R 0 – сопротивление батареи, R P – сопротивление поляризации, CP – поляризационная емкость, UP – напряжение поляризации, IL – ток нагрузки, UL – напряжение на клеммах. Математическая модель схемы описывается системой уравнений (1).
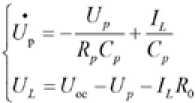
.
Определение параметров батареи. В модели эквивалентной схемы Тевенина из-за напряжения U OC аккумуляторной батареи сопротивление резистора батареи R 0 , сопротивление поляризации RP и поляризационная емкость CP изменяются вместе с УЗ, поэтому необходимо определять параметры при различных состояниях системы. Определение напряжений разомкнутой цепи рассмотрены в статье Hu, X., S. Li и H. Peng [23]. Результаты испытаний отражены на рис. 2.
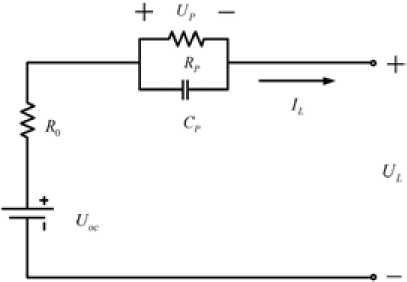
Рис. 1. Эквивалентная схема замещения Тевенина
Fig. 1. Thevenin equivalent circuit model
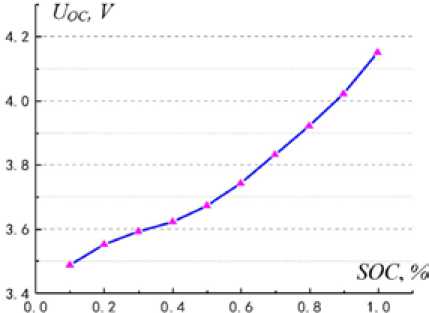
Рис. 2. Связь между напряжением разомкнутой цепи и УЗ
Fig. 2. Relationship between open circuit voltage and SOC
Как видно на рис. 2, напряжение UOC разомкнутой цепи батареи имеет зависимость от УЗ, как показано в соотношении (2):
or(S,YX') = 10,0366- SOC* -30,29.; SOC* i 34.3393 SIX'' - -17,2678 S(X': 4 4.I212-WX4 3.2I57.
Чтобы получить параметры батареи при различных состояниях УЗ, проведен гибридный импульсный характеристический тест (тест HPPC) при 25 °С. Параметры определены с помощью метода наименьших квадратов при разных начальных состояниях УЗ [24]. Результаты испытаний показаны на рис. 3.
На рис. 3 видно, что в середине двух стадий разряда постоянного тока происходит 60-секундный импульсный процесс заряда и разряда (1 С ). Он может быть использован для определения внутренних параметров каждой стадии УЗ.
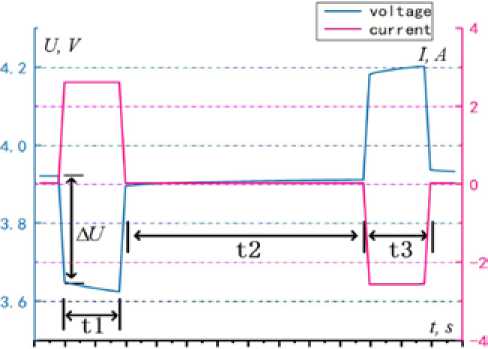
В качестве примера принят УЗ = 0.8, кривые тока и напряжения 60-секундного импульс -ного эксперимента изображены на рис. 4.
Как видно на рис. 4, процесс делится на четыре этапа: фаза разряда, пауза для разгрузки разряда, этап зарядки, пауза для разгрузки заряда. Резкое падение напряжения в фазе разряда батареи вызвано в основном сопротивлением аккумуляторной батареи R 0, так как напряжение на RC -контуре не изменяется мгновенно. Процесс разряда в промежуток времени 1 1 в основном вызван за счет изменений напряжения RC -звена U P . Тогда промежуток времени 1 1 может рассматриваться как начальное состояние RC -звена, уравнение напряжения (3)
и^кДх-е ,/R'c')
и АЛ=и, ^soc)-up (/) - //ysoc)
На этапе разгрузки разряда, а именно в момент времени t 2, ток нагрузки равен нулю, напряжение изменяется медленно, в основном на конденсаторе поляризации C P и поляризационном сопротивлении RP RC -звена. Тогда промежуток времени 1 2 можно рассматривать как нулевой входной сигнал RC -звена, уравнение напряжения (4)
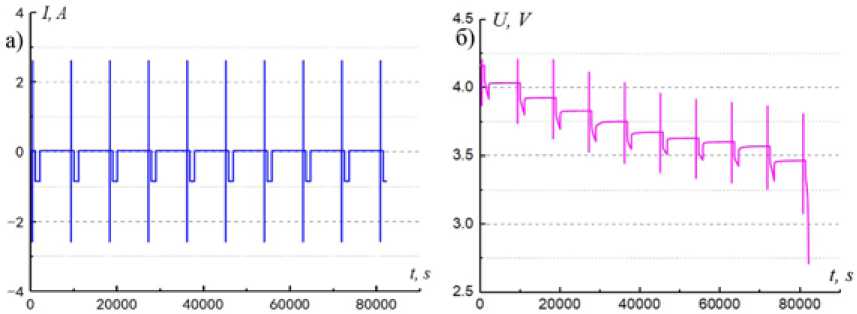
Рис. 3. Кривые тестирования HPPC: a – кривая тока; б – кривая напряжения
Fig. 3. Hybrid Pulse Power Characterization test curves: a – the current curve; б – the voltage curve
О 5 10 1 5 20 25 30 35 40 45 50 55 60 65 70
Рис. 4. Импульсное тестовое напряжение и кривые тока при УЗ = 0,8
Fig. 4. SOC = 0.8, the pulse test voltage and current curves
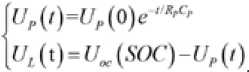
Объединив уравнения (3) и (4), используя метод наименьших квадратов, получим сопротивление поляризации RP и поляризационную емкость CP . Процесс определения параметров омического сопротивления и сопротивления поляризации показан на рис. 5. Результаты определения параметров омического сопротивления и сопротивления поляризации представлены в табл. 1.
Проверка модели. Чтобы проверить точность модели эквивалентной схемы батареи, модель эквивалентной схемы Тевенина получена с помощью программного обеспечения MATLAB
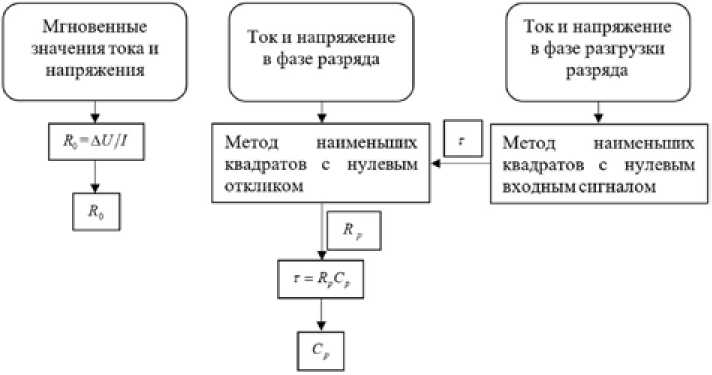
Рис. 5. Процесс определения параметров
Fig. 5. The identification process of parameters
Таблица 1. Полученные результаты теста
Table 1. Identification results of the parameters
|
УЗ |
R 0 (Ω) |
R P (Ω) |
C P ( F ) |
|
0.2 |
0.08900 |
0.04424 |
1633.9 |
|
0.4 |
0.08588 |
0.02499 |
1403 |
|
0.6 |
0.08675 |
0.02767 |
1096.5 |
|
0.8 |
0.08558 |
0.06476 |
754.4 |
|
1 |
0.08534 |
0.02302 |
1563.9 |
, , , I, s
О 20000 40000 80000 80000 01°0 ,0000 40000 60000 80000
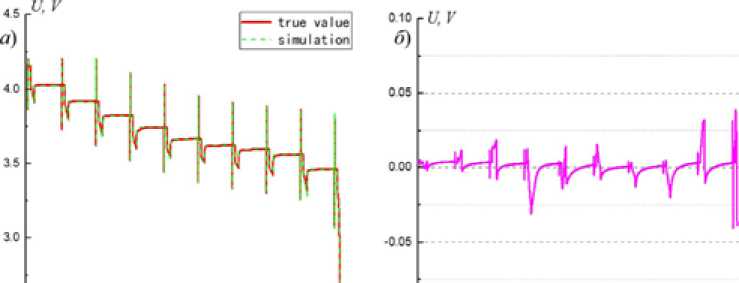
Рис. 6. Кривая напряжения и кривые ошибок: a – сравнение кривых напряжения; б – ошибка по определению напряжения
Fig. 6. Voltage contrast curve and error curves: а – the comparison curves of voltage; б – voltage error
Simulink, а проверка объективности модели проводилась в сравнении с данными импульсного теста. Результаты моделирования и фактические кривые напряжения и кривые ошибок показаны на рис. 6. Видно, что в данных HPPC расчетное значение напряжения модели в основном согласуется с результатом теста, а максимальное значение ошибки составляет 0,04874 В, среднее значение – 0,005653 В, а стандартное отклонение – 0,006269 В. Результаты показывают, что модель эквивалентной схемы Тевенина может точно отражать рабочее состояние батареи и оценку УЗ можно выполнять на этой основе.
Оценка заряда батареи
Стандартный фильтр Калмана – это алгоритм фильтрации, основанный на минимальной среднеквадратичной дисперсии, которая применима к измерению состояния линейных систем, а ошибка соответствует распределению Гаусса. Однако на практике многие системы имеют некоторую нелинейность, которая проявляется в нелинейности уравнения состояния или уравнения измерения, и стандартный алгоритм фильтра Калмана не дает удовлетворительных результатов. В этом случае решение состоит в линейной аппроксимации нелинейного соотношения, т.е. преобразования нелинейной задачи в линейную.
Алгоритм расширенного фильтра Калмана. Дискретные нелинейные динамические уравнения могут описываться уравнениями состояния и наблюдения, как показано в уравнениях (5) и (6):
хы=ДхкА^^к , (5)
U4
где xk – переменная состояния; uk – управляющая переменная; yk – наблюдаемая переменная; f ( x k , u k ) - нелинейное уравнение состояния; g ( x k , u k ) - нелинейное уравнение наблюдения; w k -системный шум; vk – наблюдаемый шум, предполагая, что wk и vk – гауссовский белый шум, и они независимы друг от друга, а их ковариация – Q и R соответственно. Здесь является априорной оценкой, x k , ■ - апостериорная оценка x k . Использование расширения Тэйлора для уточнения нелинейной модели системы в каждой точке состояния ( x k , u k ) для получения уравнений (7) и (8)
/ ( Хк , Кк ) = f(Xk , и к) + Л (хк - X^ ), К ( Хк .«4 ) * К<Хк . «4 ) + С 4 ( ^4 - Хк )
Предположим, что
, = ^А) с = ^U^J
<Х т. * * 8хм е^
Тогда уравнение (5) можно записать в виде
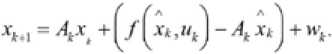
Уравнение (6) можно записать как
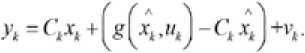
Оценка УЗ на основе алгоритма расширенного фильтра Калмана. Выражение УЗ показано в уравнении (11) [26]:
f ' n l.dt
(||)
В формуле η – эффективность процесса заряда-разряда, IL – ток в реальном времени (при разряде, I L > 0, заряд, I L < 0), C - номинальная емкость батареи.
Уравнение (11) дискретизируется, время выборки равно Δ t для получения уравнения (12). Здесь A t = 1 5 ,
Согласно определению УЗ и схемному уравнению модели батареи, получим уравнение дискретного пространственного состояния модели батареи:
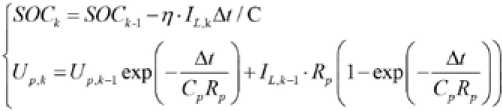
-
Переменная состояния определяется как
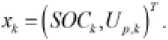
Уравнение наблюдения:
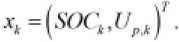
Наблюдаемая переменная определяется как
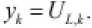
Тогда:
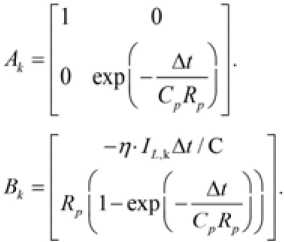
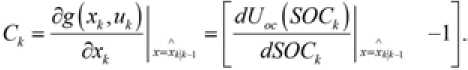
Таким образом, процесс оценки УЗ, основанный на алгоритме EKF, может быть представлен, как показано на рис. 7. Начальными входными значениями являются SOC (0), напряжение поляризации U P (0), начальная ковариация ошибок P (0), дисперсия системного шума Q и измеренная дисперсия шума R . До запуска алгоритма EKF определяют параметры эквивалентной схемы и УЗ. Когда УЗ оценивается согласно EKF, параметры модели определяют в соответствии с начальным значением УЗ. Параметры модели, рабочий ток и напряжение подставляют в рекурсивное уравнение EKF, и затем параметры модели обновляются в реальном времени в соответствии со значением измененного УЗ.
Анализ результатов моделирования и эксперимента
Чтобы проверить правильность алгоритма EKF для оценки УЗ, в работе выбран цикл дви- жения ТС в Китае и согласно NEDC. В качестве объекта исследования принят полимерный ЛИА. Для сравнения УЗ, полученного алгоритмом EKF, с реальным изменением УЗ параметры алгоритма EKF определяются, как показано в уравнении (21):
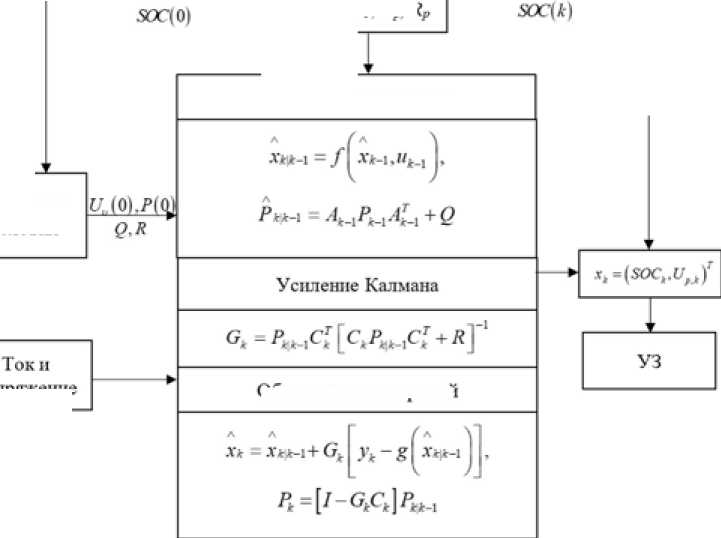
напряжение
Рис. 7. Схема алгоритма оценки алгоритма на основе EKF
Обновление времени
Начальные условия
Обновление измерении
Fig. 7. EKF-based SOC estimation algorithm flow chart
Условия зарядки и разряда батареи по выбору и расчету. Для оценки УЗ с использованием алгоритма EKF в работе выбраны циклы движения в Китае и NEDC, изображенные на рис. 8.
Согласно исследованию [29], принято, что 25 % энергии торможения пассажирского автомобиля поступает в аккумулятор. Параметры расчета электрических пассажирских транс-
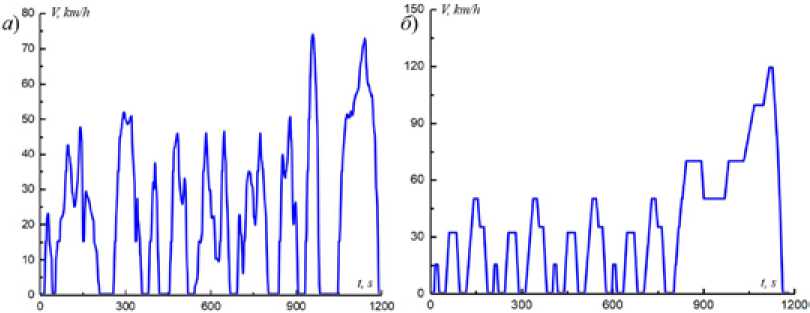
Рис. 8. Цикл движения ТС: a – в Китае; б – NEDC
Fig. 8. Road condition: a – in China; б – NEDC
Таблица 2. Параметры легкового автомобиля
Сопротиежние качению Fr- 0.0076 4 0.000056u,
Сопротивление ВОПуХ)’ /С-^СИ^
Сопротивление ОТ уклона F. -mgsncr
Сопротивление ускорению Fj - Sma
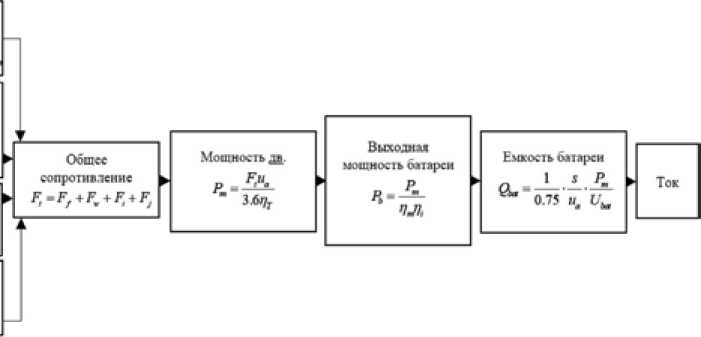
Рис. 9. Блок-схема расчета тока нагрузки в ячейке
Table 2. The parameters of the passenger car
|
Параметр |
Размерность |
Величина |
|
Масса ТС |
кг |
1500 |
|
Коэффициент сопротивления воздуха |
0.4 |
|
|
Площадь передней части |
м2 |
2 |
|
Плотность воздуха |
кг/м3 |
1.2258 |
|
КПД трансмиссии η T |
0.96 |
|
|
Коэффициент сопротивления качению |
0.0076+0.000056u a |
Fig. 9. Single cell battery load current calculation flow chart портных средств приведены в табл. 2. Чтобы получить ток нагрузки на одну ячейку, здесь использован метод расчета, показанный на рис. 9.
В соответствии с моделью выходная мощность двигателя электропривода определяется следующим уравнением:
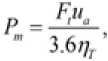
где F t – полное сопротивление транспортного средства, которое состоит из сопротивления качению F f , сопротивления воздуха Fw , сопротивления уклона Fi и сопротивления ускорения F j ; u a – скорость транспортного средства, км/ч.
В соответствии с выходной мощностью Pm двигателя привода выходная мощность Pb аккумулятора может быть получена с учетом КПД двигателя η m и КПД преобразователя DC/DC η i как
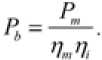
Здесь среднее КПД двигателя η m принято 85 %, среднее КПД преобразователя η i 85 % [29]. Постоянное напряжение составляет 320 В. Для удовлетворительной динамики и дальности пробега ЭТС рассчитана мощность аккумуляторной батареи. В статье рассчитана энергоемкость аккумуляторной батареи при движении на расстояние 200 км. Полезная емкость, рассчитанная как 75 % от общей емкости аккумулятора, определяется выражением
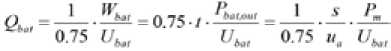
,
где ua – эквивалентная скорость транспортного средства; s – дальность хода; Pm – мощность потребления тягового двигателя ( W ); P bat,out – выходная мощность батареи; U bat – напряжение на клеммах аккумулятора; Wbat – энергоемкость аккумулятора; Qbat – емкость аккумулятора.
Согласно уравнению (24), с учетом того, что максимальный разрядный ток полимерного ЛИА не может превышать 2 C (5,2 А), требуемая емкость аккумулятора составила 88,4 А·ч. В комбинации с выбранными параметрами батареи, показанными в табл. 3, рассчитана структура батареи – 89 последовательных, 34 параллельных батареи. Ток в одиночной ячейке согласно условиям Китая и NEDC представлен на рис. 10.
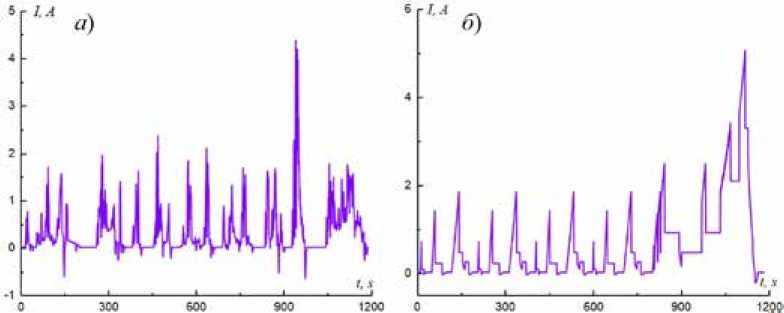
Рис. 10. Ток в одиночной ячейке: а – в Китае; б – NEDC
Fig. 10. Single cell load current of а – сhinacar, б – NEDC
Таблица 3. Параметры одиночной ячейки NCR 18650
Table 3. Single battery NCR 18650 parameters
|
Параметры |
Размерность |
Значение |
|
Номинальная емкость |
мА·ч |
2600 |
|
Номинальное напряжение |
В |
3.6 |
|
Максимальное напряжение |
В |
4.2 |
|
Минимальное напряжение |
В |
2.75 |
|
Вес |
г |
45 |
|
Диапазон рабочих температур |
ºС |
-20…+60 |
Анализ результатов. Используя алгоритм EKF в оценке заряда батареи, упомянутый в статье, получили экспериментальное и наблюдаемое значение напряжения на клеммах аккумулятора, показанные на рис. 11, при условии движения в Китае.
При сравнении наблюдаемого и экспериментального напряжений, изображенных на рис. 11, максимальная погрешность составила 0,18 В, средняя ошибка 0,01396 В. Таким образом, применяя эквивалентную схему Тевенина в условиях дороги Chinacar, алгоритм EKF может обеспечить более точное вычисление предельного напряжения.
В NEDC напряжение на клеммах аккумулятора, полученное в эксперименте и в результате наблюдения, показано на рис. 12. При сравнении наблюдаемого и экспериментального напряжения максимальная погрешность составила 0,185 В, средняя ошибка 0,01767 В. Можно видеть, что при использовании эквивалентной схемы Тевенина в NEDC применение алгоритма EKF может обеспечить более точное вычисление предельного напряжения.
Чтобы проверить правильность предложенного алгоритма EKF, проведено сравнение результатов оценки УЗ, полученных алгоритмом, с результатами кулонометрического метода в дорожных условиях Китая, как показано на рис. 13, из которого видно, что при дорожных условиях в Китае оценка УЗ батареи практически совпадает с реальным изменением. Макси-
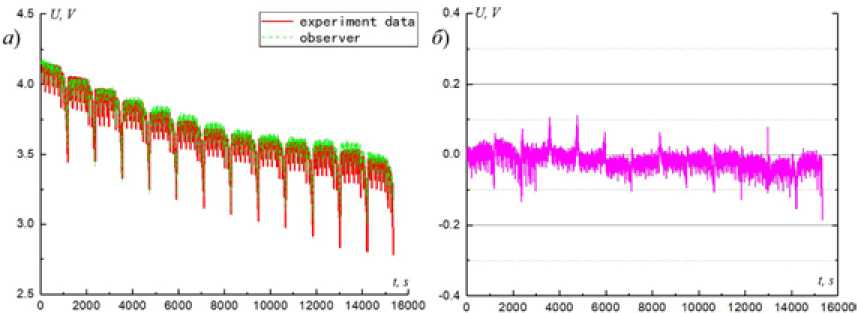
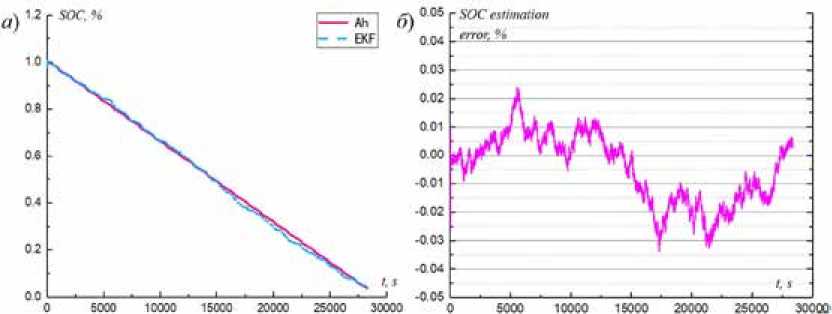
Рис. 12. Сравнение кривых напряжения а ) и ошибки б ) в NEDC
Fig. 12. The comparison curves of a) terminal voltage and б) error in NEDC мальная ошибка УЗ составляет 3,38 %, а средняя ошибка 1,042 %. В NEDC результат оценки УЗ, полученный алгоритмом, сравнивается с результатами, полученными кулонометрическим методом, как показано на рис. 14.
Как видно на рис. 14, для NEDC с применением алгоритма EKF оценка УЗ батареи практически совпадает с реальным изменением. Максимальная ошибка определения заряда составляет 3,138 %, средняя ошибка 1,138 %. Здесь алгоритм EKF используется в дорожных условиях Китая и NEDC. Результаты оценки состояния заряда показывают, что максимальная ошибка оценки УЗ составляет не более 4 %, а средняя ошибка – 2 %. Для проверки надежности предложенного алгоритма изменено начальное значение УЗ в алгоритме EKF в двух условиях и установлено начальное значение УЗ 0,9, 0,8 и 0,6 соответственно. Фактическое начальное значение УЗ батареи равно единице, тогда начальные абсолютные погрешности будут равны 0,1, 0,2 и 0,4 соответственно. В дорожных условиях Китая с EKF рассчитанные и реальные УЗ показаны на рис. 15.
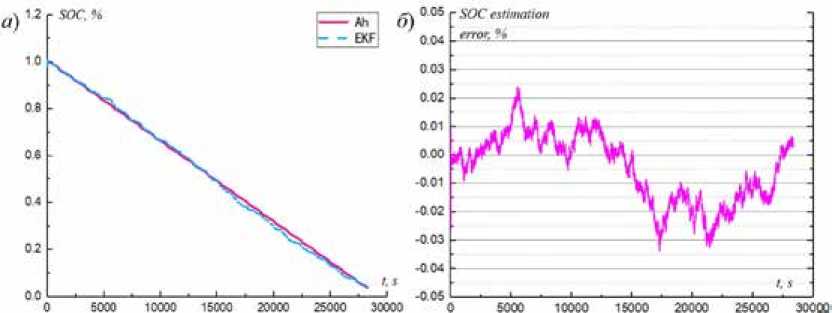
Рис. 13. Сравнение и оценка кривых УЗ в Китае: а – кривая изменения УЗ; б – ошибка по определению УЗ
Fig. 13. The SOC estimation comparison and error curves in Chinacar: а – the SOC estimation comparison; б – error curves
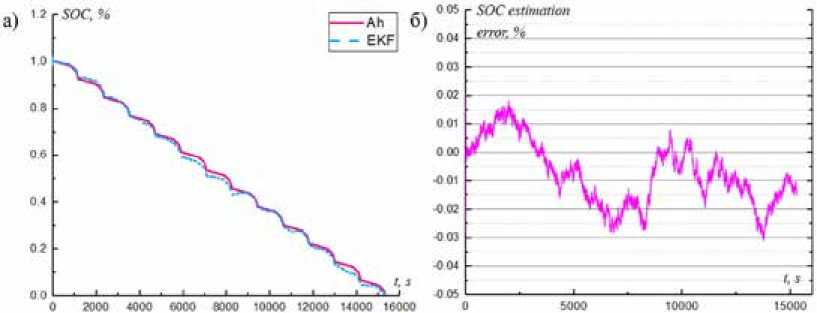
Рис. 14. Сравнение и оценка кривых УЗ в NEDC: а – кривая изменения УЗ; б – ошибка по определению УЗ
Fig. 14. The SOC estimation comparison and error curves in NEDC: a – the SOC estimation comparison; б – error curves
Из зависимостей, представленных на рис. 15, видно, что в начале значения УЗ при различных условиях имеют высокое отклонение, однако после 200 с они сходятся к реальному значению, что указывает на сильную устойчивость алгоритма EKF, способности устранить начальную ошибку и более быструю сходимость к истинному значению при значительном отклонении. Результаты расчета УЗ в NEDC алгоритмом EKF и реальные изменения УЗ отражены на рис. 16. Видно, что в начале значения УЗ разных начальных положений имеют большое отклонение, однако после 100 с они сходятся к реальному значению, что указывает на сильную устойчивость алгоритма EKF, способность устранить начальную ошибку и более быструю сходимость к истинному значению при значительном отклонении. Результаты оценки УЗ показывают, что начальная ошибка будет большой, но в случае начального состояния через 100 с быстро сходится к истинному значению, что отражает хорошую сходимость и стабильность. Из этого следует, что применение алгоритма EKF для оценки УЗ имеет достаточную защиту от шумов.
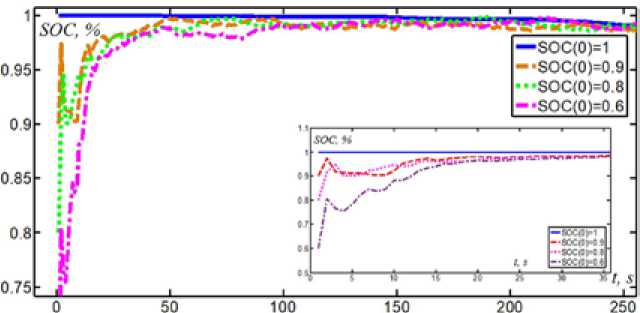
Рис. 15. Устойчивость EKF для разных исходных значений УЗ в дорожном цикле Китая
Fig. 15. The robustness of EKF for different SOC initial values in Chinacar
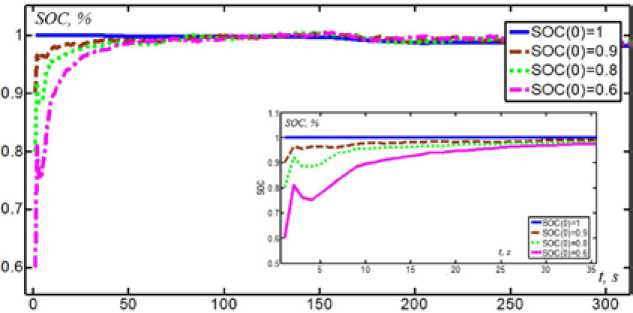
Рис. 16. Устойчивость алгоритма EKF для разных начальных значений УЗ в NEDC
Fig. 16. The robustness of EKF for different SOC initial values in NEDC
Заключение
В работе проведен анализ различных методов определения заряда химических накопителей энергии, установленных на электротранспортном средстве, в частности: на основе поляризации Нернста; на основе нейронной сети, модифицированной эквивалентной схемы замещения; в форме дискретных по времени состояний; на основе модели эквивалентной RC-схемы третьего порядка и ряда других. Показано, что применение алгоритма расширенного фильтра Калмана для определения уровня напряжения аккумуляторной батареи и последующего расчета величины заряда аккумулятора на основе схемы Тевенина позволяет получить ряд преимуществ: в производительности вычислений и быстроте сходимости. Предложенная методика расчета степени заряженности аккумуляторной батареи апробирована для двух циклов движения транспортного средства: экспериментального цикла, характерного для Китая, и цикла NEDC. Расчетные значения напряжения аккумуляторной батареи сопоставлены с результатами реальных измерений и получены следующие основные выводы:
-
1. Показано, что оценка напряжения с использованием предложенной методики отличается от реально измеренного значения в среднем на 0,1 В.
-
2. Апробация методики оценки степени заряженности аккумуляторной батареи для двух циклов движения показала удовлетворительную сходимость: среднее значение ошибки составило 2 % при максимальной погрешности не более 4 %.
-
3. Доказано, что предложенный алгоритм расчета напряжения аккумуляторной батареи на основе модифицированного фильтра Калмана обладает преимуществом по производительности и скорости сходимости, а также значительной стойкостью к помехам.
Благодарность / Acknowledgement
Исследование выполнено при финансовой поддержке РФФИ и ГФЕН Китая в рамках научного проекта № 20-58-53055 «Исследование влияния форсированных и тяжелых циклических режимов заряда и разряда на физико-химические характеристики функциональных материалов и ресурса литиевых аккумуляторов».
The study was sponsored by RFBR and NSFC in China as part of a research project № 20-5853055 «Investigation of the effect of the forced and heavy cyclic charge and discharge modes for the physicochemical characteristics of functional materials and the life of lithium batteries».
Список литературы Определение уровня заряда литий-ионного аккумулятора на основе алгоритма расширенного фильтра Калмана
- Dubarry, M., N. Vuillaume and B.Y. Liaw, From single cell model to battery pack simulation for Li-ion batteries. Journal of Power Sources, 2009. 186(2): p. 500-507.
- Борисевич А.В., Моделирование литий-ионных аккумуляторов для систем управления батареями: обзор текущего состояния. Научно-практический журнал Современная техника и технологии, 2014, 5(33) - Режим доступа: http://technology.snauka.ru/2014/05/3542 - Заглавие с экрана. - Access: http://technology.snauka.ru/2014/05/354
- Андреев А.А., Возмилов А.Г., Калмаков В.А. Моделирование работы литий-ионного аккумулятора в суровых климатических условиях. Труды научно-технической конференции Пром-Инжиниринг, 2015, c. 181-184..
- He, H., R. Xiong and J. Fan, Evaluation of Lithium-Ion Battery Equivalent Circuit Models for State of Charge Estimation by an Experimental Approach. Energies, 2011, 4(12): p. 582-598.
- Xiong, R., et al., Model-based state of charge and peak power capability joint estimation of lithium-ion battery in plug-in hybrid electric vehicles. Journal of Power Sources, 2013. 229: p. 159-169.
- He, W., et al., State of charge estimation for Li-ion batteries using neural network modeling and unscented Kalman filter-based error cancellation. International Journal of Electrical Power & Energy Systems, 2014. 62: p. 783-791.
- Tian, Y., et al., A modified model based state of charge estimation of power lithium-ion batteries using unscented Kalman filter. Journal of Power Sources, 2014. 270: p. 619-626.
- Печенко В.В. Динамическая модель ячейки аккумуляторной батареи с единственным состоянием. Радиотехника, 2015. 4: 58-60.
- Скрипко Л.А. Расчет степени износа литийионных аккумуляторов, используемых в батарейных системах электромобилей гибридных автомобилей, 2017. 3: 2-4.
- Mu, H., R. Xiong and F. Sun, A Novel Multi-model Probability Based Battery State-of-charge Fusion Estimation Approach. Energy Procedia, 2016. 88: p. 840-846.
- Zhang, Y., R. Xiong and H. He, Evaluation of the Model-based State-of-Charge Estimation Methods for Lithium-ion Batteries. IEEE Transportation Electrification Conference and Expo (ITEC), 2016: p. 1-8.
- LI Zhe, LU Languang, OUYANG Minggao, Comparison of methods for improving SOC estimation accuracy through an ampere-hour integeration approach. J Tsinghua Univ(Sci&Tech), 2010(08): p.1293-1296+1301.
- Roscher, M.A. and D.U. Sauer, Dynamic electric behavior and open-circuit-voltage modeling of LiFePO4-based lithium ion secondary batteries. Journal of Power Sources, 2011. 196(1): p. 331-336.
- He, H., et al., State-of-Charge Estimation of the Lithium-Ion Battery Using an Adaptive Extended Kalman Filter Based on an Improved Thevenin Model. IEEE Transactions on Industrial Electronics, 2011: p. 1461-1469.
- A. Zenati, P.D.A.H., Estimation of the SOC and the SOH of Li-ion Batteries, by combining Impedance Measurements with the Fuzzy Logic Inference. Proc. 36th Annu. Conf. IEEE Ind. Electron. Soc, 2010: p. 1773-1778.
- Ng, K.S., et al., Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Applied Energy, 2009. 86(9): p. 1506-1511.
- Chiang, Y., W. Sean and J. Ke, Online estimation of internal resistance and open-circuit voltage of lithium-ion batteries in electric vehicles. Journal of Power Sources, 2011. 196(8): p. 3921-3932.
- Bernd, T., M. Kleutges and A. Kroll, Nonlinear Black Box Modelling - Fuzzy Networks versus Neural Networks. Neural Computing & Applications, 1999. 8(2): p. 151 - 162.
- Auger, F., et al., Industrial Applications of the Kalman Filter: A Review. IEEE Transactions on Industrial Electronics, 2013. 60(12): p. 5458-5471.
- Lin Chengtao, Qiu Bin&Chen Quanshi, A Comparative Study on Power Input Equivalent Circuit Model for Electric Vehicle Battery. Automotive Engineering, 2006: p.229-234.
- Kim, J. and B.H. Cho, State-of-Charge Estimation and State-of-Health Prediction of a Li-Ion Degraded Battery Based on an EKF Combined With a Per-Unit System. IEEE Transactions on Vehicular Technology, 2011. 60(9): p. 4249-4260.
- Hu, X., S. Li and H. Peng, A comparative study of equivalent circuit models for Li-ion batteries. Journal of Power Sources, 2012. 198: p. 359-367.
- State-of-Charge Estimation of the Lithium-Ion Battery Using an Adaptive Extended Kalman Filter Based on an Improved Thevenin Model.
- WEI Xuezhe, SUN Zechang, TIANJiaqing, Parameter Identification and State Estimation of Li-ion Power Battery in Hybrid Electric Vehicle. JOURNAL OF TONGJI UNIVERSITY (NATURAL SCIENCE), 2008: p.231-235.
- Plett, G.L., Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs. Journal of Power Sources, 2004. 134(2): p. 252-261.
- Plett, G.L., Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs. Journal of Power Sources, 2004. 134(2): p. 262-276.
- Plett, G.L., Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs. Journal of Power Sources, 2004. 134(2): p. 277-292.
- Yuan, S., H. Wu and C. Yin, State of Charge Estimation Using the Extended Kalman Filter for Battery Management Systems Based on the ARX Battery Model. Energies, 2013. 6(1): p. 444-470.
- Tourani, A., P. White and P. Ivey, Analysis of electric and thermal behaviour of lithium-ion cells in realistic driving cycles. Journal of Power Sources, 2014. 268: p. 301-314.
- Xu, L., et al., Optimal sizing of plug-in fuel cell electric vehicles using models of vehicle performance and system cost. Applied Energy, 2013. 103: p. 477-487.
- Song, Z., et al., Optimization for a hybrid energy storage system in electric vehicles using dynamic programing approach. Applied Energy, 2015. 139: p. 151-162.


