Определение усилий в стрежнях фермы в процессе колебаний

Предлагается алгоритм динамического расчета статически неопределимой плоской стальной фермы в процессе её колебаний, вызванных нестационарной нагрузкой. При этом рассматриваются колебаний неповрежденной и поврежденной конструкции.

Алгоритм решения задачи реализуется с помощью метода временного анализа конструкций (МВА), основанного на непосредственном решении обыкновенного дифференциального уравнения (ОДУ) движения дискретной диссипативной системы[1]:

MY( t ) + CY ( t ) + KY ( t ) = P ( t ), (1) где M = diag( m 1 , ..., m „ ), C = C ^T = ( с Д K = ( r_M ) e M n ( R ) -матрицы масс, демпфирования и жесткости; Y ( t ), P ( t ) e M n ,1 ( R ) - векторы перемещений и внешних воздействий.

В результате интегрирования ОДУ (1) определяются кинематические параметры реакции: перемещения, скорости и ускорения (соответственно векторы Y ( t ), Y ( t ), Y ( t ) ).На их основе можно получить силовые параметры реакции - инерционные I , диссипативные F и восстанавливающие R силы:

I ( t ) = - MY ( t ), F ( t ) = CY ( t ), R ( t ) = KY ( t ). (2) Эти кинематические и силовые параметры реакции будут возникать в дискретных точках - в узлах конструкции, связанных со степенями свободы. В этих же узлах собраны массы m i .

На практике возникает необходимость знать не только параметры реакции, но и усилия, и напряжения, возникающие в элементах конструкции, поэтому необходимо перейти от перемещений узлов к усилиям.

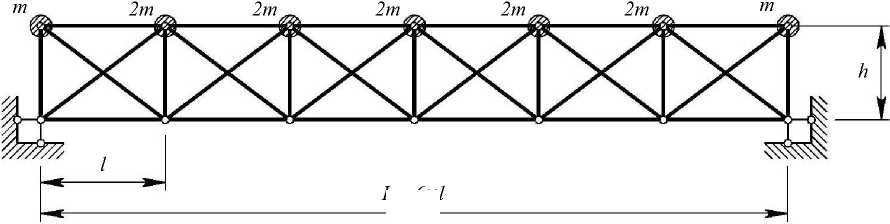
Рассмотрим вначале алгоритм решения задачи на примере неповрежденной плоской стальной фермы (рис. 1).

Для удобства расчетов выразим все размеры фермы через длину панели 1 : h = 0,75 1 , длина раскоса 1 1 = 1,25 1 ; жесткости элементов - через жесткость стоек EA : жесткость поясов EA 1 = k 1 - EA , жесткость раскосов EA ₂ = k ₂- EA .

Более подробно параметры фермы описаны в работе [3].

В соответствии с расчетной схемой степень статической неопределимости фермы q = 7. Для решения задачи воспользуемся методом сил, основная (ОС) и эквивалентная (ЭС) системы для которого изображены на рис. 2.

Каноническое уравнение метода сил в матричной форме имеет вид L • X + A p = 0, где L - матрица податливости, связанная с матрицей жесткости K соотношением L = K "¹; A p - вектор свободных членов. Соответственно вектор усилий в лишних связях X из этого уравнения равен:

X = — L • A p = — K • A p . (3)

L = 6× l

Рис. 1. Расчетная схема плоской стальной фермы

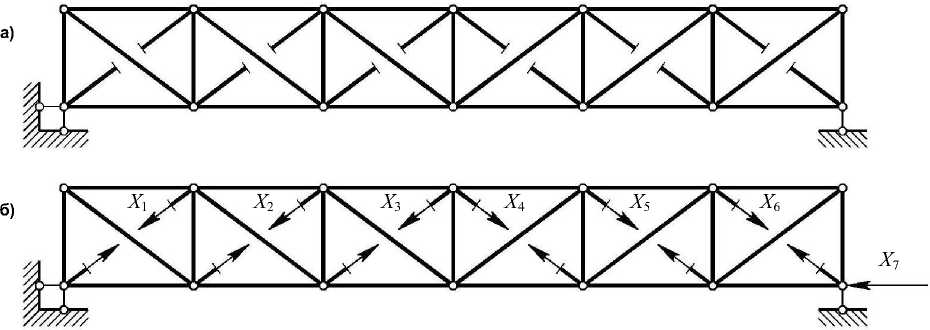
Рис. 2. Основная (а) и эквивалентная (б) системы метода сил

Для          получения          матрицы

L = ( b y ) ( i , j = 1,..., q ) необходимо построить единичные эпюры продольных сил N i в ОС от действия сил X i = 1 (рис. 3) и определить перемещения 5 ij ^.

В силу регулярной структуры решетки в расчетной схеме единичные эпюры Ni от неизвестных Xi = 1 (i = 1,..., 6) имеют однотипный харак тер и локализуются внутри i-й панели (рис. 3, а). Эпюра Ni от неизвестного X7 = 1 показана на рис. 3, б.

Для определения перемещений by воспользу емся формулой Максвелла

s = 31

ik jk k j = ъ м где s - количество стержней фермы. Тогда полу чим:

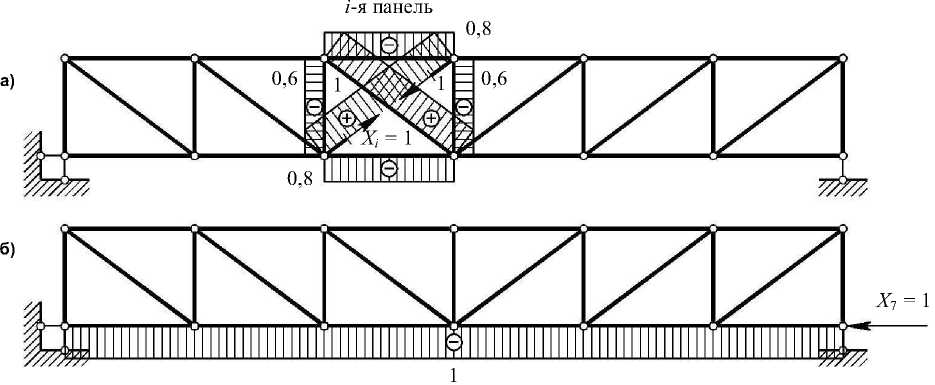
Рис. 3. Эпюры единичных продольных сил в ОС:

а - от усилий X i = 1 ( i = 1,..., 6) ; б - от усилия X 7 = 1

⁵ ii = “( i = 1,..., 6),

EA

⁵ i , i + i = ⁵ i + 1, i = ^р 44 ( i = 1’-’5)’ ,          , _EA

5i7 = 57i = Y4 (i = 1’-’6)’ 577 = П4 , EA              EA а = 0,54 +128 + 25, P = 0,27, k1    k2

Y = 0, ⁸/ k 1 , П = 1 k i .

Структура матрицы L размерностью q X q в

этом случае имеет вид: "а P 0 0 0 0 y " P а P 0 0 0 y 0 P а P 0 0 Y L = (5,) = — • ij    EA 0 0 р а р 0 y .   (4) 0 0 0 р а P Y 0 0 0 0 р а Y _ Y Y Y Y Y Y П] При матричной формулировке задачи будем иметь l = NT • B • N, (5) где N(s X q) - массив, в столбцах которого содер жатся единичные продольные усилия в стержнях

ОС, полученные при действии сил Х_; = 1

(i = 1,..., q); B(sX s) - диагональная матрица не связанных между собой элементов фермы. Диаго нальные элементы матрицы

B -

l i

( EA ) i

( i = 1,..., s ).

По аналогии с формулой (5) вычислим вектор ^A p ^:

Ap = NT • B • Np ,

где N p ( s X 1) - вектор усилий в стержнях ОС от действия внешнего воздействия,

N p = [ N 1 p N 2 p ... N 31 p ] T .

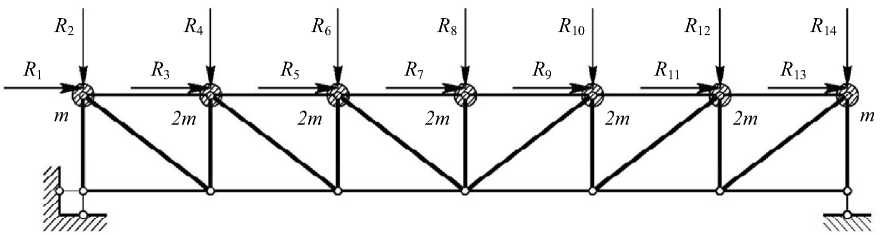
В общем случае вынужденных колебаний фермы в узлах, содержащих массы mi, действуют восстанавливающие, инерционные, диссипативные и внешние силы (согласно уравнению (1)). Для получения вектора Np необходимо выполнить расчет фермы на действие восстанавливающих сил, которые можно представить в виде R(t) = P(t) -1(t) - F(t) (для случая свободных колебаний силы R запишутся в виде R(t) = -1(t) - F(t)). Учитывая, что число динамических степеней свободы n = 14, расчетная схема фермы для этого случая будет иметь вид, представленный на рис. 4.

Векторы усилий N_p и сил R ( n X 1 ) образуют систему линейных алгебраических уравнений:

N p = A • R , (7)

где A = ( a ij ) ( i = 1,..., s ; j = 1,..., n ) - матрица переходных коэффициентов.

Далее для определения усилий в лишних связях воспользуемся формулой (3), подставив в ее правую часть выражения (6) и (7):

X = - L ¹ •A _p = - K • N T • B • A • R = C • R , (8) где C = - K • N T • B • A - матрица коэффициентов размерностью q X n .

Окончательные продольные усилия в стержнях N_0K согласно принципу суперпозиции будут определяться по формуле N_OK = N • X + N_p . Подставив (7) и (8) в это выражение, получим:

NOK =- N • C • R + A • R =

= ( - N • C + A ) • R = U • R , (9) где U = - N • C + A - матрица коэффициентов размерностью s X n .

В выражении (9) матрица U не зависит от времени и связана только с геометрическими и физическими параметрами конструкции. Вектор R , напротив, является функцией времени R = R ( t ), поэтому в процессе колебаний будем получать вектор усилий в элементах фермы, также являющийся функцией от времени N_OK ( t ).

Рассмотрим теперь случай обрушения конструкции, когда происходит выключение одного из раскосов фермы, например, раскоса в пятой панели (рис. 5). В этом случае число стержней s уменьшится на единицу, в результате степень статической неопределимости q будет равна 6.

2m

2m

R 5

R 7

R 9

m

R 2

R 1

m

R 4

R 3

2m

R 6

R 8

R ₁₀

R ₁₂

R ₁₄

R 11

^R 13

2m

2m

Рис. 4. Расчетная схема фермы с восстанавливающими силами

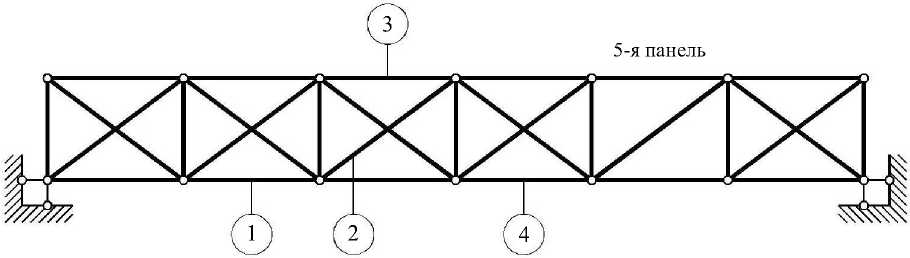
Рис. 5. Расчетная схема фермы после обрушения раскоса

Расчетные формулы для фермы с удаленным раскосом строятся аналогично предыдущим с учетом того, что размерности q и 5 основных массивов уменьшатся на единицу путем удаления строки и столбца, соответствующих номеру выключенного элемента (раскоса) фермы. В частности, матрица податливости фермы будет получена из (4) путем удаления 5-й строки и 5-го столбца. Удаление этих строки и столбца обусловлено тем, что в расчетной схеме выключенный раскос совпадает с 5-й лишней связью (см. рис. 2, б).

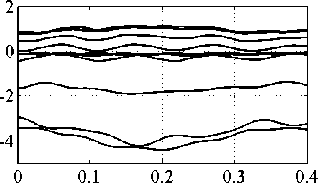
В статье [2] показана работа поврежденной фермы с расчетной схемой на рис. 5. При помощи МВА были получены осциллограммы узловых перемещений фермы y k (рис. 6, а). Описанный алгоритм позволил определить усилия N k в стержнях фермы в процессе колебаний. Осциллограммы усилий в отмеченных на рис. 5 элементах, показаны на рис. 6, б.

Выводы

Построен алгоритм решения задачи перехода от узловых перемещений статически нагруженной

У к , см

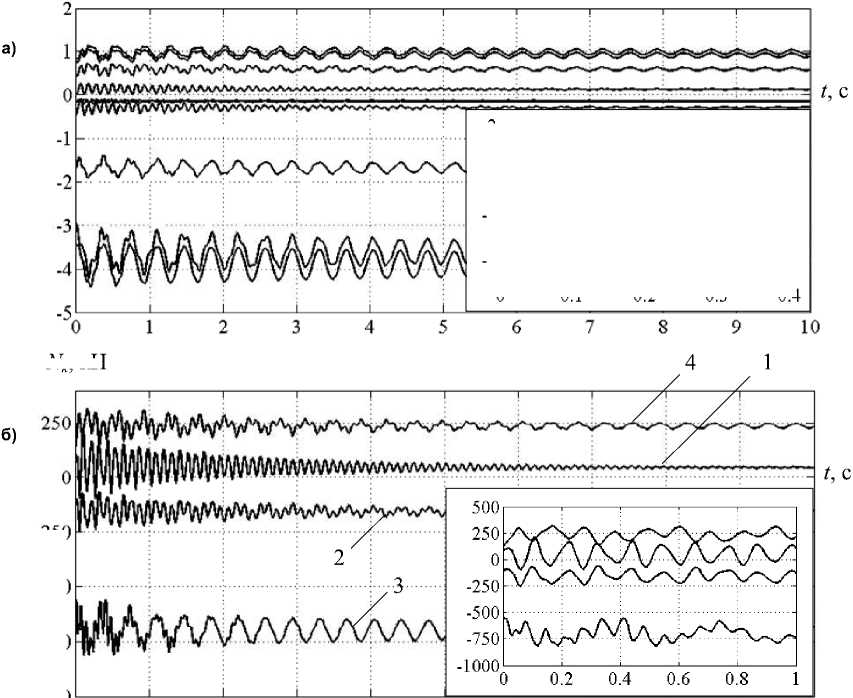
N k , кН

-250

-750

S

Рис. 6. Осциллограммы узловых перемещений (а) и усилий в стержнях (б) фермы

-500

.юооо

фермы к усилиям и напряжениям в её элементах. Данный алгоритм можно реализовать в задаче колебаний фермы при выключении (обрушении) отдельных несущих элементов.

В качестве достоинства алгоритма стоит отметить его простоту, а также легкость реализации в вычислительных комплексах, таких как MATLAB.