Определение вероятностных характеристик технических средств связи центров ситуационного управления

Стремительное развитие современных технологий в области телекоммуникаций позволяет использовать новые формы организации управления на их основе. Повышение эффективности принятия управленческих решений обеспечивается консолидацией информационных ресурсов в едином центре, примером которых могут служить центры ситуационного управления [1]. Данные центры представляют собой высокотехнологичные комплексы, включающие в себя разнообразные технические средства приема-передачи, обработки и хранения данных, проведения видеоконференцсвязи, информационные и информационно-аналитические системы и обслуживающий персонал. В частности ситуационные центры могут создаваться для размещения оперативных штабов органов внутренних дел при возникновении кризисных ситуаций. При этом наибольшее значение приобретают средства связи, обеспечивающие наиболее эффективное функционирование сотрудников ситуационных центров, например, с помощью развертывания и использования транкинговых систем связи, что в частности является одним из приоритетных направлений развития систем профессиональной подвижной радиосвязи [2]. Однако осуществление выбора технических средств, обеспечивающих эффективную обработку поступающих данных в полной мере, не возможно без построения соответствую- щих математических моделей и методов. Одним из возможных подходов решения данной задачи является использование аппарата теории массового обслуживания [3, 4].

Аппарат теории массового обслуживания

Поскольку современные технические средства связи (ТСС) могут обладать возможностью постановки в очередь поступающих вызовов (в терминологии теории массового обслуживания – заявок, под заявкой будем понимать присылаемый запрос о необходимости выполнения определенных действий для его обслуживания), причем очередь ограничивается только возможностями ТСС, то систему связи можно считать смешанной системой массового обслуживания.

Определим, каким условиям должны отвечать ТСС для их использования в центрах ситуационного управления. Для этого будем считать поток заявок простейшим, а число поступивших заявок за интервал времени τ , распределенным по закону Пуассона

где λ – интенсивность поступления заявок.

1 - старший преподаватель Воронежского института МВД России.

В частности, вероятность, что за время τ не поступит ни одной заявки, определяется как

Будем считать, что длительность обслуживания tоб одной заявки также распределена по показательному закону с плотностью распределения определяемой как где μ – интенсивность обслуживания заявок.

Одним из требований к транкинговым системам подвижной радиосвязи органов внутренних дел является наличие трех категорий приоритета обслуживания: высшего, первого и второго. При поступлении заявки высшей категории, ТСС приостанавливает обслуживание абонентов первой и второй категорий с постановкой их на ожидание. При поступлении заявки первой категории, ей предоставляется приоритет по отношению к заявкам второй категории. Заявки второй категории обслуживаются без приоритетов, при занятости ТСС заявка становится в очередь. Вероятность одновременного поступления заявок одного типа будем считать пренебрежимо малой, и учитывать ее не будем.

Найдем выражения, позволяющие определить вероятностные характеристики работы ТСС, обладающего одним местом в очереди, s = 1 .

Будем считать, что на вход системы поступает простейший поток с интенсивностями:

λ₀ – для заявок высшей категории,

λ₁ – для заявок первой категории, λ₂ – для заявок второй категории.

Независимо от типа заявки интенсивность обслуживания будем считать одинаковой для всех и равной μ . Введем обозначение состояние ТСС в виде:

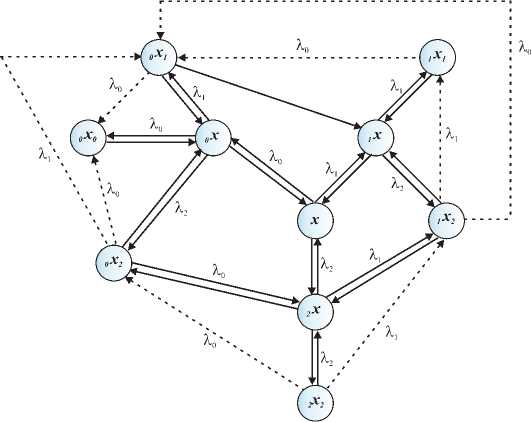
Рис. 1. Граф состояний ТСС axb ,                                                                   (4)

где a = 0, 1, 2 – категория обслуживаемой заявки, b = 0, 1, 2 – категория заявки, поставленной в очередь. Следовательно, обозначению 0x0 соответствует состояние ТСС, при котором обслуживается вызов высшей категории и один вызов этой же категории поставлен в очередь, обозначению x – отсутствие заявок в ТСС.

Построим схему переходов ТСС в виде графа в соответствии с требованием к транкинговым системам подвижной радиосвязи, рассмотренным выше.

Для упрощения графического представления смены состояний ТСС на рис. 1 не отображены петли, имеющиеся у каждой вершины и соответствующие отсутствию смены состояний. Пунктиром проведены дуги графа, при использовании которых происходит потеря заявки, находящейся в очереди. Веса дуг показывают интенсивность поступления заявок соответствующих категорий. Вес необозначенных дуг равен интенсивности обслуживания μ . Дугами показаны разрешенные переходы, а возможность перескока через состояния, например, из ₂ х ₂ в х за малый промежуток времени, будем считать величиной высшего порядка малости по сравнению с вероятностью разрешенных переходов.

Рассмотрим вероятности нахождения системы в каждом состоянии

p(t), 0p(t), 1p(t), ..., apb(t) .

Очевидно, что для любого момента времени

Зафиксировав момент времени t найдем вероятность p(t + Δt) того, что в момент t + Δt система будет находиться в состоянии х . Это может произойти следующими способами:

• ♦    А — в момент t система находилась в состоянии х , и за время Δt не перешла из нее ни в ₀х (не пришло ни одной заявки высшей категории), ни в ₁х (не пришло ни одной заявки первой категории), ни в ₂х (не пришло ни одной заявки второй категории);

• ♦    В — в момент t система находилась в состоянии 0х , а за время Δt перешла из нее в х (заявка была обслужена);

• ♦    С — в момент t система находилась в состоянии 1х , а за время Δt перешла из нее в х (заявка была обслужена);

• ♦    D — в момент t система находилась в состоянии ₂х , а за время Δt перешла из нее в х (заявка была обслужена).

По теореме сложения вероятностей имеем

p(t + Δt) P(A) + P(B) + P(C) + P(D)                       (6)

Вероятность того, что в момент t система была в состоянии х равна p(t) . Вероятность того, что за время Δt не придет заявка высшей категории, равна , первой категории – , второй категории –     .

По теореме умножения вероятность того, что не придет ни одна из них g~Vf g-^ g-^t = g_(A)+^i+^2)A'

С точностью до величин высшего порядка малости

Следовательно,

Найдем вероятность события В. Вероятность, что система находилась в состоянии 0х, равна 0p(t). Вероятность того, что за время Δt вызов был обслужен, равна          с точнос тью до малых величин высшего порядка:

Следовательно,

Р^=ор^рМ

Аналогично для событий С и D

Р^С^ ~ {р^pAt,P^D^ = 2Р^ pAt.

Отсюда получаем, что i+ ор^ pAt + iP^t) pAt + 2p(t) pAt или рУ + At^ = p^ — p^y^Xtt + Л, +^)A/ + ,+ Р^‘(оР(^+ 1P^V lP(f^

Перенося p(t) в левую часть, деля на Δt и переходя к пределу при Δt → 0 , получим дифференциальное уравнение для p(t) :

Аналогичные дифференциальные уравнения могут быть составлены и для других вероятностей состояний.

Синтез систем уравнений

Процесс составления уравнений вида (7) для решения данной задачи можно упростить. Введем обозначения: _av_b – вершина графа, соответствующая состоянию _ax_b , ♦ E v ( a v b ) — множество входящих дуг вершины a v b , ♦ E_is(_av b ) — множество исходящих дуг вершины a v b , ♦ V v ( a v b ) — множество вершин v , смежных с a v b , соединенных с помощью входящих в вершину _av_b дуг,

• ♦    ^v(e) – вес дуги e ,

• ♦    p( a v b ) — вероятность состояния a x b , Тогда

tMftG)=

dt

Составив систему уравнений в соответствии с (8) и указав начальные условия

РкА=Х’ аРьк1^^^а'Ь'

интегрированием можно получить значения всех вероятностей. Полученные вероятности можно использовать для расчета относительной и абсолютной пропускной способности ТСС, вероятности отказа в обслуживании и др. Поскольку планируется, что ТСС будет работать постоянно, то, несомненно, будет интересным предельный установившийся режим обслуживания заявок. Поскольку такой режим существует для любой системы с отказами [4], найдем пределы рассматриваемых вероятностей. Для этого заменим в системе из уравнений (8) производные нулями, а вероятности соответствующими пределами этих вероятностей. Тогда получим систему не из дифференциальных, а из алгебраических урав- нений вида

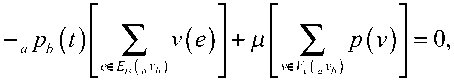
для решения которой необходимо добавить условие (9).

Заключение

Решение полученной системы уравнений (и подобным ей при других условиях) позволит определить значения предельных вероятностей всех состояний _ax_b , среднее время ожидания начала обслуживания, вероятность отказа и другие характеристики системы связи. Однако оценку эффективности обработки заявок можно осуществить, зная лишь вероятность нахождения системы в «наихудшем» состоянии, при котором поступающие заявки на обслуживание будут отклонены (в рассматриваемом случае такому состоянию соответствует ₀x₀ , т.е. когда обслуживаются и находятся в очереди заявки с высшим приоритетом). Вероятность отказа в предельном случае можно найти в соответствии с [4] следующим образом: _{Q =}      (^Ло/^)²      _{= t} _      ^о/А< + 1

(Л0/а<) +Л0/р + 1 (Ло/р) +Ло/^ + 1

В то же время для оптимизации выбора ТСС можно задать минимальное значение вероятности появления наихудшего случая ₀p₀ и предложить решения по его изменению, например, путем увеличения мест в очереди каждого ТСС или увеличением числа ТСС, используемых в ситуационных центрах