Определение ветровой нагрузки на арочную конструкцию
Бесплатный доступ
В статье рассматриваются вопросы воздействия ветровой нагрузки на арку. Представлен алгоритм определения ветровой нагрузки.
Ветровая нагрузка, арка, алгоритм
Короткий адрес: https://sciup.org/140278431
IDR: 140278431
Текст научной статьи Определение ветровой нагрузки на арочную конструкцию
Рассмотрим определение ветровой нагрузки на арочную конструкцию на примере здания комплекса теннисных кортов. Комплекс представляет собой арочное однопролетное здание с размерами в плане 60х120 м. Арки двухшарнирные параболического очертания, проектируются из стального двутавра 80Б1 с шагом 3 м. Стрела подъема арок назначена с учетом необходимых для теннисной игры высотных параметров. Автором статьи рассмотрены два варианта стрелы подъема арок: 30 и 15 м.
Определение ветровой нагрузки на арочные конструкции осуществляется в соответствии со СП 20.13330.2011 «Нагрузки и воздействия» [1]. Нормативное значение ветровой нагрузки w определятся как сумма средней w m и пульсационной w p составляющих.
Рассмотрим определение средней составляющей. Нормативное значение средней составляющей ветровой нагрузки определяется как произведение нормативного значения ветрового давления w o , коэффициента, учитывающего изменение ветрового давления в зависимости от высоты плотности застройки k(z e ) и аэродинамического коэффициента c. Как известно, нормативное значение ветрового давления определяется в зависимости ветрового района, принимаемого по карте 3 приложения Ж СП [1]. Здание комплекса проектируется в городе Оренбурге, который относится к III ветровому району. Коэффициент, учитывающий изменение ветрового давления в зависимости от высоты и плотности застройки , был определен по таблице 11.2 [1] для типа местности В и эквивалентной высоты. Ветровая нагрузка для арочных конструкций, не имеющих стен, принимается по упрощенной схеме, приведенной на рисунке 1.
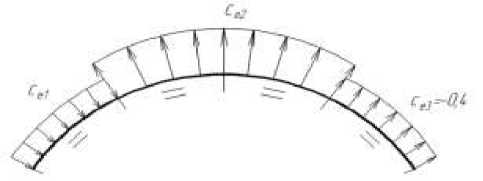
Рисунок 1. Схема распределения ветрового давления на поверхности арочной конструкции
Согласно схеме распределения ветрового давления на сводчатые и близкие к ним по очертанию покрытия, криволинейная поверхность арки разбита на три зоны: зона активного давления, занимающая часть с наветренной стороны и равная четверти длины кривой, две другие - зоны пассивного давления: центральная зона, длиной в половину длины кривой, и зона в подветренной стороне, симметричная зоне активного давления.
Величину интенсивности ветрового давления при прочих равных условиях определяет аэродинамический коэффициент с. Числовые значения аэродинамического коэффициента в пределах каждой зоны постоянны. При этом при переходе из одной зоны в другую аэродинамический коэффициент изменяется скачком, а при переходе из зоны активного давления в центральную зону – даже с переменой знака.
Для определения пульсационной составляющей ветровой нагрузки необходимо выяснить частоту собственных колебаний. Применительно воспользуемся формулой А.И. Ленченко, приведенной в книге «Устойчивость и динамика сооружений в примерах и задачах» Безухова Н.И [2].
Наименьшая частота колебания арки определяется по формуле:
"= в j
( β 2-1)( β 2-1- c 2)
к (в 2 +3) '
где β – параметр, определяемый по формуле:
π β=α, a - угол в радианах, определяемый согласно рисунку 2.
c – параметр, определяемый по формуле:
•=j
0-R 3 EI ,
R – радиус арки, определяемый согласно рисунку 2;
q – нагрузка от собственного веса арки в кН/м;
E – модуль упругости стали, по таблице Г.10[3];
I – момент инерции, для двутавра 80Б1 I =199,5·10-5 м4.
Л - параметр, определяемый по формуле:
m∙R 4
λ= EI , m – масса одного метра арки, определяемая по формуле:
ρ∙A m = — , (5)
p - плотность стали, p=78,5 кН/м3;
А – площадь сечения арки, А= 203,2·10-4 м2;
g – ускорение свободного падения, g= 9,8 м/сек2.
fl
a «
Рисунок 2. К определению радиуса и угла арки
Приближенно для параболической арки радиус определяется по формуле:
f L 2
R=2+f • (6)
где f – стрела подъема арки;
L – пролет арки.
Поскольку полученные для двух вариантов первые частоты собственных колебаний co больше предельного значения собственной частоты f1 нормативное значение пульсационной составляющей ветровой нагрузки определяется как произведение нормативной средней составляющей ветровой нагрузки wm, коэффициента пульсации давления ветра Z(ze) и коэффициента пространственной корреляции пульсации ветра v.
Коэффициент пульсации давления ветра определяется по таблице 11.4 [1] в зависимости от эквивалентной высоты и типа. Коэффициент пространственной корреляции пульсации ветра определяется по таблице 11.6 [1].
Расчетная ветровая нагрузка действует перпендикулярно поверхности арочного покрытия и определяется по формуле:
q » = (w m + w P ) •Y f' Y n' B , (7)
Согласно п.11.1.12 [2] коэффициент надежности по ветровой нагрузке принимается равным 1,4.
Результаты расчета ветровой нагрузки приведены в таблице 1.
Таблица 1 – Результаты расчета
|
Параметр |
15 м |
30 м |
||||
|
1 зона |
2 зона |
3 зона |
1 зона |
2 зона |
3 зона |
|
|
wm , кН/м2 |
0,114 |
-0,271 |
-0,114 |
0,296 |
-0,445 |
-0,148 |
|
wp кН/м2 |
0,086 |
-0,203 |
-0,086 |
0,187 |
-0,281 |
-0,093 |
|
w, кН/м2 |
0,2 |
-0,474 |
-0,2 |
0,483 |
-0,726 |
-0,241 |
|
q w , кН/м |
0,84 |
-1,991 |
-0,84 |
2,03 |
-3,05 |
-1,01 |
Как показывают результаты расчета, при прочих равных условиях, увеличение стрелы подъема арки в 2 раза увеличивает расчетную ветровую нагрузку на 59 % в зоне активного давления, на 35 % в центральной зоне и на 17 % в зоне пассивного давления с подветренной стороны. При этом максимальное усилие для пятнадцатиметровой арки составит 22,4 кН/м, для тридцатиметровой - 51,05 кН/м.
Список литературы Определение ветровой нагрузки на арочную конструкцию
- СП 20.13330.2011 «Нагрузки и воздействия».
- Безухов, Н.И. Устойчивость и динамика сооружений в примерах и задачах: учеб. пособие для вузов / Н.И. Безухов, О.В. Лужин, Н.В. Колкунов. М.: Стройиздат, 1969. 424 с.
- СП 16.13330.2011 «Стальные конструкции».


