Определение вязкости жидкости по методу Стокса

Определение вязкости является важным шагом в разработке и оптимизации процессов в различных отраслях промышленности, таких как нефтеперерабатывающая промышленность, химическая промышленность, энергетика и другие.

Метод определения вязкости жидкости по Стоксу - это один из наиболее распространенных и надежных методов, который позволяет получать результаты с высокой точностью. Метод основан на измерении времени течения жидкости через капилляр с известным диаметром и давлением.

Экспериментальное исследование динамики движения тел в вязкой среде представляет собой фундаментальный подход к пониманию физических свойств жидкостей и их взаимодействия с погруженными объектами. Один из классических методов, метод Стокса, позволяет определить коэффициент вязкости жидкости, наблюдая за скоростью падения маленьких сферических объектов в жидкости. Этот метод основан на теоретических предположениях, что движение тела происходит в режиме ламинарного течения, и что силы сопротивления, действующие на тело, пропорциональны его скорости.

Результаты исследования

Вязкость - это свойство жидкости сопротивляться деформации сдвига ее слоев. Механизм возникновения вязкости обусловлен тем, что при течении жидкости вдоль твердой стенки скорость ее слоев в результате торможения потока различна, вследствие чего между слоями возникает сила трения [1,2,3]. Эта сила называется силой внутреннего или вязкого трения, которая определяется формулой Ньютона.

F = Т * dv * S , dx

где ] - коэффициент динамической вяз-dv кости; — - изменение скорости между слоями; S - площадка соприкосновения разных слоев жидкости.

Жидкость рассматривается как непрерывная бесструктурная среда в теоретическом описании вязкости. Частицы в равновесном состоянии будут расположены в соответствии равновесной силы, которая будет ровна нулю. Не соблюдение этого приводит к перемещению частиц относительно друг друга до состояния равновесия [2, 4].

В вязкой среде при движении тел возникают силы сопротивления.

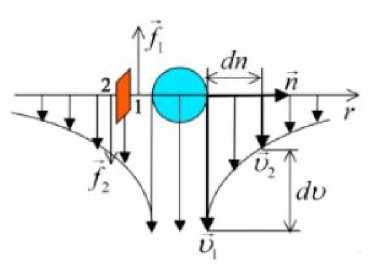
Рис. 1. Твердый шарик, движущийся вниз в жидкой среде

На рисунке изображена схема движущегося шарика вниз в жидкой среде со скоростью V1 .

На смачиваемой данной жидкость поверхность тела всегда есть прилипший слой, совершающий действия вместе с телом с той же V1. В следствие этого возникает трение между этим слоем и слоями жидкости вокруг шарика. Огибающая де- монстрирует профиль скорости вязкой жидкости в окрестности шарика (рис. 1). На движущийся шарик в жидкости действуют три силы: выталкивающая сила, сила тяжести, сила сопротивления.

Величина сопротивления для сферической формы определяется по формуле Стокса:

F_c = 6*77*r*r*v   ,        (2)

Где r - вязкость жидкости; r - радиус шарика; v - скорость движения.

Определение выталкивающей силы и силы тяжести осуществляется следующим образом:

Где r - радиус шарика; р - плотность шарика; р₀ - плотность жидкости.

Эти силы постоянны, а сила сопротивления прямо пропорциональна скорости и меньше силы тяжести на начальном этапе.

F_T=477r³pg,            (3)

F_B=477r³p_og,          (4)

При увеличении силы сопротивления уравновешиваются все три силы [5]. Начинается равномерное движение шарика:

^F T = ^F B + ^F c ,

или 4 nr³ pg = 4 nr³ p₀g + 6nrrv ,

откуда r =

2r²g(p-p o ) 9v

Для проведения эксперимента по определению вязкости по методу Стокса необходимо иметь специальное устройство -стеклянную капиллярную трубку с шариком внутри (рис. 2), на сосуде изображены две метки А и В на расстоянии l друг от друга. Шарик известного радиуса роняется в жидкость, и с помощью измерения времени t, за которое шарик опустится на определенное расстояние I = AB.

До начала эксперимента было установлено расстояние от уровня жидкости до верхней метки l = 22 см = 0,22 м.

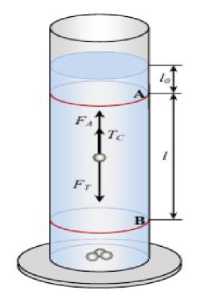
Рис. 2. Лабораторная установка

С помощью подстановки выражения для скорости движения и замены радиуса шарика r на диаметр d можно преобразовать формулу (4):

d²g(p-p o )t

⁷         181

.

Были проведены измерения и определен коэффициент вязкости. В таблице 1 приведены результаты измерений и вычислений при использовании 5 шариков различного диаметра d, измеренных с помощью микрометра.

Таблица 1. Результаты измерений и вычислений вязкости жидкости по методу Стокса

№	d , м	t , c	l , м	Коэффициент вязкости 77, Па*с	7 общ , Па*с	Абсолютная погрешность, Лг	Относительная погрешность, %
1.	0,00229 0,00228 0,00224 0,00681 d=   3 = 0,00227	3,24	0,22	0,013	0,01496	-0,00196	0,87
2.	0,00195 0,00198 0,0021 d= 0,00201	5,38		0,017		0,00204	1,14
3.	0,00177 0,00177 0,0019 d =0,0018	4,94		0,013		-0,00196	0,87
4.	0,0023 0,0024 0,0024 d = 0,00236	4,41	0,22	0,0195	0,01496	0,00454	1,3
5.	0,00116 0,00195 0,00193 d =0,00168	5,45		0,0123		-0,00266	0,82

Преимущества метода

Преимущества метода Стокс заключаются в следующем:

• 1.    высокая точность и репродукция результатов;

• 2.    простота и доступность оборудования;

• 3.    широкий диапазон измеряемых концентраций жидкости;

• 4.    возможность измерения вязкости жидкости в широком диапазоне температур.

Ограничения метода

Ограничения метода Стокс следующие:

• 1.    необходимость точного контроля температуры и давления жидкости;

• 2.    ограничения по размерам капилляра и длине измерительного участка;

• 3.    необходимость точного измерения времени течения жидкости;

• 4.    ограничения по концентрации частиц и примесей в жидкости.

Заключение

Проведенный эксперимент по методу Стокса позволил не только подтвердить определить коэффициент вязкости исследуемой жидкости при разном диаметре шариков. Полученные данные имеют важное значение для различных прикладных областей, включая инженерию, медицину и фармацевтику, где знание вязкости жидкостей необходимо для проектирования эффективных систем и технологий. Эксперимент подчеркивает значимость фундаментальных исследований в области физики жидкостей и открывает новые возможности для дальнейших исследований в этой области.

Чтобы получить точные результаты, необходимо проводить эксперименты по методу Стокса с особой тщательностью и теоретические предположения о характере в соответствии с установленными стандар-движения тел в вязкой среде, но и точно тами и методиками.