Определение влияния параметров источника питания на резонансный режим работы вентильного электропривода колебательного движения

В настоящее время к современным электроприводам углового колебательного движения предъявляются все более жесткие требования относительно энергетических показателей и точности позиционирования исполнительного органа [1–3].

Одним из рациональных способов повысить эффективность работы электропривода колебательного движения является построение его на базе двухфазного вентильного двигателя, работающего непосредственно в режиме вынужденных колебаний за счет фазовой модуляции питающих напряжений с обеспечением резонансного режима. Как известно, при этом инерционные и упругие силы в электромеханической системе взаимно уравновешиваются, а энергия возбудителя колебаний расходуется только на преодоление диссипативных сил [4–6].

Очевидно, что энергетически выгодный резонансный режим работы вентильного электропривода может достигаться за счет регулирования механических, либо электрических параметров системы [1, 7, 8]. Причем последнее является более предпочтительным, так как не требует дополнительного введения в систему позиционной нагрузки в виде торсионов или пружин.

Целью данной статьи является определение

влияния электрических параметров источников питания на резонансный режим работы вентильного электропривода при фазовом способе возбуждения колебательного режима работы.

Для этого необходимо решить следующие задачи:

– аналитически определить выражения и разработать методику для расчета выходных параметров вентильного электропривода колебательного движения;

– на основании полученных выражений провести оценку угловой координаты положения подвижного элемента привода от параметров источника питания с учетом обобщенной нагрузки на валу двигателя;

– построить графики зависимостей амплитудного значения координаты от фазного напряжения вентильного двигателя при разных значениях частоты колебаний и определить зависимость последней в функции от напряжения.

Математическая модель вентильногоэлектропривода колебательного движения

Для упрощенного математического описания вентильного электродвигателя используется система координат d – q , жестко связанная с ротором, при этом ось d совмещается с направлением магнитного поля статора.

Электромеханические системы

В этом случае система дифференциальных уравнений, которыми описываются электромагнитные и электромеханические переходные процессы в вентильном двигателе, имеет вид [7, 9, 10]:

di

—

® ^Lq i q ;

Ud = idRs + Ld —r dt di

Uq = iqRs + L      + m Ldid +-

^М э = Pm ^[ i q ^У m ⁺ i d i q ( ^Ld ^{— L}q ) ] = ^М н⁽ J ^m m^dt , ^m m , ddt m X

1 dmm   1

= (Мэ — Мн ),     = p dt J э н dt m где Ud, Uq, Id, Iq – напряжения и токи фазных обмоток вентильного двигателя; Rs – активное сопротивление обмотки статора; Ld, Lq – продольная и поперечная индуктивности; Ψm – максимальное потокосцепление обмотки статора с потоком ротора; ω, ωm – электрическая и механическая скорости изменения обобщенной координаты подвижного элемента; χ – угловое перемещение подвижного элемента; Мэ, Мн – электромагнитный момент и обобщенный момент сопротивления; р – число пар полюсов; m – число фаз двигателя.

Третье уравнение системы (1) описывает колебательное движение вторичного элемента вентильного двигателя и представляет собой нелинейное дифференциальное уравнение второго порядка.

Обобщенная нагрузка на валу электродвигателя колебательного движения М н является функцией параметров нагрузки привода и его движения. Наиболее часто она представляется совокупностью позиционных и инерционных сил, а также сил жидкостного и сухого трения [11, 12]:

d 2 x   „ dx                 .

Мн = Lмех   ■' RMех "Г + Cмех X + Мтр sign m , dt2 dt где Lмех – инерционная составляющая нагрузки; Rмех – демпфирующая составляющая нагрузки; Cмех – позиционная составляющая нагрузки; Мтр – момент сухого трения.

В общем случае для возбуждения колебательного режима работы статорные обмотки вентильного двигателя подключаются к источникам напряжения [13]:

U_d ( t ) = U 1 = const;

Uq (t) = U2 sIn(Q t + a), где U1 – постоянное напряжение обмотки d; U2, Ω, α – амплитудное значение, круговая частота и начальная фаза питающего напряжения по обмотке q.

Подставив выражения для фазных напряжений (3) в первые два уравнения системы (1) и решив ее относительно фазных токов обмоток d и q вентильного двигателя, получим:

i d ( t ) = U ₂ [ N ₂ cos( Q t + a ) + N ₁ sIn( Q t + a ) ] + U ₁ N 3 + N 4 ;

i_q ( t ) = U ₂ [ N 5 sIn( Q t + a ) + N 6 cos( Q t + a ) ] — U ₁ N 7 — N 8 .

Здесь значения коэффициентов N ₁ …N ₈, зависящих от параметров двигателя, частоты и скорости колебаний подвижного элемента привода, представлены в табл. 1.

Таблица 1

Коэффициенты для рассчета значений фазных токов

®L ( m ² L_dL + R_s ² — Q ² L_dL )                        —m L_qQ R_s ( L_d + L_q )

q      qs       q                        q sq

=                                                   , N7=

(m2 Ld Lq + Rs — Q2 Ld Lq )2 + Q2 Rs (Ld + Lq)       (m2 Ld Lq + Rs — Q2 Ld Lq )2 + Q2 Rs (Ld+

N =     Rs      N = —®2 Lq Уm   N = Rs (m2 Ld Lq + Rs — Q2Ld Lq) + LdQ2Rs (Ld+

• 3  m2LdLq + R2’  4  m2LdLq + R2 ’  5    (m2LdLq + Rs —Q2LdLq)2 +Q2R2(Ld + Lq)

N = L d ^{Q (} m ² L d L q ^{+ R}s ^{—q 2} L d L q ) ^— R 2 ^{Q (} L d ⁺ L q )   N =     L d m       N _   У „ R s m

• ⁶    ( m ² L d L q + R s —Q ² L d L q ) ² +Q ² R ²( L d + L q ) ,   7    m² L d L q + R s ,  ⁸   m² L d L q + R² '

После подстановки найденных значений токов (4) в уравнение для электромагнитного момента, и разложив последний в ряд Маклорена по степеням скорости m в окрестностях m = 0, получим:

М _э( m ) = М _э(0) + dM aC⁰) m + ... , d m

где М _э (0) = М _П характеризует пусковую составляющую электромагнитного момента двигателя;

dМ э (0) d ю

to = М д = F д ю - электромагнитный демпфирующий момент, F д - коэффициент электромагнитно-

го демпфирования вентильного двигателя;

M П = Р mm [^ m i q |ю= 0 + ⁽ L d ^- L q ) i d | ю= 0 i q | ю= 0 ] =

= ( U ₂ d 1 + U ₂U 1 d ₂)( 5 1 sin( Q t + а ) + Q 5 ₂ cos( Q t + а )),

^FД = Pm ^ m^ T-i q |ю= 0 ^{+ ( L}d - ^Lq 2        d IV

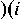
did          diq qdю|ю=0 id dю|ю=0)

= ( - U 1² k 3 + U 1 k 1 - k ₂ + U ₂ ² ( k 4 - ( k 5 cos(2( Q t + а )) - k 6 sin(2( Q t + а )).

Следует отметить, что при инженерных расчетах коэффициента электромагнитного демпфирования вентильного двигателя достаточно учесть только постоянные составляющие с коэффициентами k 1 – k 4 , так как весовой вклад составляющих модуляции не превышает 3 %.

С учетом сказанного уравнение движения подвижного элемента двигателя (2) при пренебрежении в электромеханической системе моментом сухого трения примет вид:

T    d 2 ^{X   (} R ме^{х F} Д ) d ^X Г ч M

L мех   ₂⁺       ,        ⁺ C мех ^X M П ^.

dt ²           dt

Решением уравнения (6) будет являться закон движения подвижного элемента вентильного двигателя:

X ( t ) = А sin( Q t + а ) + B cos( Q t + а ),                                                                     (7)

где составляющие амплитуды колебания можно записать как

U 1 ( h 3 C мех - hC мех Q ² ) + h 0 C мех Q 2 + C мех h 2 + Q 2 ( U 3 h 1 C мех + h 16 C мех + U 1 hn C мех ) +

A =______________________ + Q 4 ( - U 13 h i8 + U 2 h i9 + U 1 h 20 + h 21 ) __________________________

( С мех -Q ² h 24 ) ■ ( Q ² ( U 4 h 4 - U 3 h 5 + U 2 h. + U 1 h 7 + h 8 - C мех h 9 ) + h _W + C мех )

B = __^Q ( - ^U 1_ ^h 13_ ⁺_ ^U 1_ ^h L4^_ ^U 1( ^C мех h 12_ ⁺_ ^h 22 2 ⁺_ ^C мех h 11 ⁺_ ^h 2з)__

Q ² ( U ⁴ h 4 - U 3 h 5 + U 1² h 6 + U 1 h 7 + h 8 - C мех h 9 ) + h _W + C мех ^.

Здесь h ₀… h ₂₄ – коэффициенты, зависящие от параметров вентильного двигателя, источника питания по обмотке q и нагрузки.

Тогда выражение для амплитудного значения координаты подвижного элемента вентильного двигателя при отсутствии позиционной нагрузки ( C _мех = 0) будет иметь вид:

X m

Q 2 ( - U 13 h 18 + U 1² h 19 + U 1 h 20 + h 21 )      Y

\(- h 2 ₄ ■ ( Q ² ( U 1⁴ h ₄ - U 1³ h ₅ + U 1² h 6 + U 1 h 7 + h 8 ) + h ₁₀)

'     Q ( - U 13 h 13 + U 1² h 14 + U 1 h 22 + h 23 )

^ Q² ( U ⁴ h 4 - U 1 h 5 + U ² h 6 + U 1 h 7 + h § ) + h 10

Полученные выражения (7)–(9) являются теоретической основой для расчета выходных параметров и рабочих характеристик вентильного электропривода колебательного движения. Они также могут быть использованы при оценке динамических и энергетических показателей электропривода [14, 15].

На основании анализа выражения (9) можно утверждать, что существует условие поддержания максимального значения амплитуды колебаний подвижного элемента вентильного двигателя за счет регулирования собственной частоты привода в заданном диапазоне изменения частоты ω путем изменения напряжения U 1 .

Для определения этого условия необходимо определить скорость изменения подвижного элемента вентильного двигателя, взяв первую производную по времени от выражения (7), и подставить в уравнение для электромагнитного момента (5). После алгебраических преобразований алгоритм регулирования собственной частоты вентильного электропривода колебательного движения будет иметь вид:

U 1 ( Q ) =

2^ Q ² d 1 -Q d ₂ + d 3 ■ cos

arccos

Q ³ d ₄ +Q ² d ₅ +Q d 6 + d ₇

■J ( Q d 8 + Q d 9 + d 10 )

Q

- d ₁₁

^{+ d} 12

где d1…d12 – коэффициенты, зависящие от параметров вентильного двигателя, источника по обмотке q и нагрузки.

Электромеханические системы

Анализ результатов расчета

Для оценки предложенной методики расчета выходных параметров вентильного электропривода колебательного движения и условия обеспечения регулирования его собственной частоты были проведены расчеты в математической среде MathCAD 2000. В качестве расчетной модели был выбран вентильный электродвигатель, параметры которого представлены в табл. 2 [9, 16–18].

Для данного двигателя, согласно изложенной методике, были рассчитаны выходные параметры и построены зависимости амплитудного значения координаты положения от фазного напряжения U1 при разных значениях частоты колебаний Ω (рис. 1) и алгоритм регулирования напряжения U1 с целью поддержания резонансного режима работы колебательной электромеханической системы (рис. 2).

Полученные графики наглядно иллюстрируют зависимость амплитудно-частотных характеристик электропривода от величины одного из фазных напряжений вентильного двигателя, что позволяет разработать практические схемы электроприводов колебательного движения с регулируемой собст-

Таблица 2

Параметры	R s	L d	Lq	т m	J	p	m
Единицы измерения	Ом	Гн	Гн	Вб	Кг·м2	–	–
Значения	0,96	5,25e-3	2,25e-3	0,183	13e-3	4	3

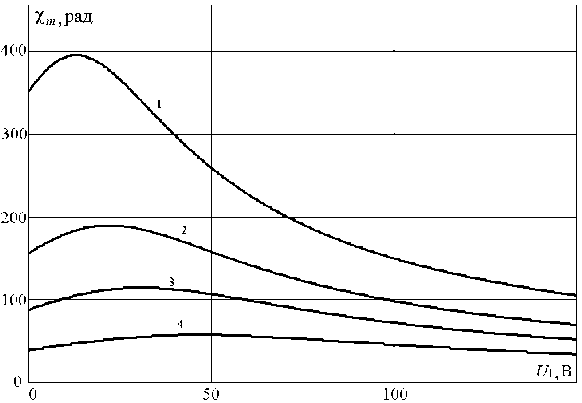
Рис. 1. График зависимости амплитудного значения координаты от фазного напряжения вентильного двигателя: 1 – Ω = 2 рад/с;

2 – Ω = 3 рад/с; 3 – Ω = 4 рад/с; 4 – Ω = 6 рад/с

Рис. 2. Алгоритм поддержания резонансного режима работы вентильного электропривода колебательного движения при регулировании частоты Ω

венной частотой для поддержания энергетически выгодного резонансного режима работы без применения электромеханической обратной связи по положению [19, 20].

Заключение

Применение безредукторных электроприводов колебательного движения с регулируемой собственной частотой, выполненных на базе вентильных электродвигателей, работающих непосредственно в режиме периодического реверса за счет фазовой модуляции питающих напряжений, позволяет обеспечить практически весь потребный диапазон частот и ускорений при высоких энергетических показателях. Как показали исследования, оценку их выходных характеристик целесообразно проводить по изложенной выше методике, ограничиваясь при расчетах только постоянными составляющими электромагнитного демпфирующего момента. С целью поддержания резонансного режима работы практические схемы электроприводов должны содержать в своей структуре функциональный преобразователь напряжения, реализующий программно или схемотехнически алгоритм (10).