Определение влияния теплоотвода в медную подкладку на проплавление тонколистовых материалов при аргонно-дуговой сварке

При освоении технологии сварки новых изделий приходиться оптимизировать геометрию проплавления экспериментальным путем, поэтому все большее применение находят количественные модели сварки для расчета глубины проплавления и ширины шва. Моделирование сварки встык тонколистовых материалов на медной подкладке сопряжено с некоторыми трудностями, поскольку имеет место значительный теплоотвод в подкладку, достаточно точно определить величину которого без экспериментов невозможно. Для получения расчетной модели с экспериментальными коэффициентами, описывающей реальное влияние теплоотвода на ширину стыкового шва при аргонно-дуговой сварке на медной подкладке проводилось сравнение расчетного поля температуры, полученного при численном моделировании, с экспериментально измеренными значениями температуры.

Для описания температурного поля T(x, y, z, t) в плоском образце размером 50x100x2 мм использовали дифференциальное нелинейное уравнение теплопроводности:

с ( Т )р( Т Т ) — = Я ( Т ) д t

д ² T  д² T   д ² T

++ дx 2   ду 2   дz 2

где ρ(T) – плотность, кг/м3; λ(T) – коэффициент теплопроводности, Вт/(мxK); с(Т) – удельная теплоемкость, Дж/(кг·°С). Зависимость теплофизических свойств стали от температуры ρ(T), λ(T), с(Т) принимали согласно литературным данным [4].

В использованной нами расчетной схеме сквозного проплавления тепловая мощность сварочной дуги для одной из свариваемых пластин частично вводится через ее боковую поверхность в плоскости стыка, а частично через верхнюю поверхность пластины. Изотермы температуры плавления от движущихся распределенного и сосредоточенного источников имитируют поверхность солидуса сварочной ванны T s (x, y, z)= T s . Линейный тепловой источник был задан как тепловой поток через плоскость, которая разделяет образец на 2 части (рис. 1) по формуле [1]:

. AX ,2

q,         ^-(— )

q (x, t) =----1-=exp a ,4 ah 4Л          (2)

где а – размер конечного элемента, м; h – толщина стали, м; ΔX=X 0 -V·TIME – перемещение по оси Х.

Нормально-круговой источник нагрева на верхней поверхности рассчитывался по формуле[1]:

q ( x , у , t ) = kq 2 exp^{( -} k^{( A X 2} + Y²⁾⁾,  (3)

П где k – коэффициент сосредоточенности дуги, м-2.

Граничные условия теплопередачи с внешних поверхностей определяли удельный тепловой поток при конвекции и излучении. Радиационное излучение учитывалось только на поверхности А и рассчитывалось по формуле:

q^r = sC0(T4 -Tc4), где T – температура тела; Tc – температура окружающей среды (20°С); C0 – постоянная Стефана-Больцмана C0=5,67х10-8 Вт/(м2·К4); ε – излучательная способность стали, которую принимали согласно данным работы [2].

Удельный тепловой поток при конвективном теплообмене принимали равным q 2k =25 Вт/(м²·К) по данным работы [2] для свободных поверхностей кроме А, B и D, как показано на рис. 1.

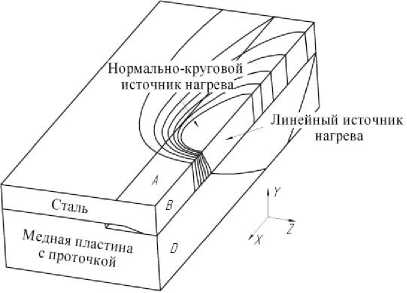
Рис. 1. Расчетная схема модели

Граничные условия контакта сталь-медь рассматривались как сумма термических проводимостей воздушной прослойки α воз между микровыступами контактируемых материалов и металлического контакта α М , для расчета которых использовали методику из справочника [3]. Термическая проводимость воздушной прослойки описывается выражением:

ос =_____^воз_____  02 • 104_____Вт___ авоз                    1,02 IV    2        , h А + h              м • град мед ь    ста ль                      р где λвоз – теплопроводность воздуха, Вт/(м·°С); hмедь – микронеровность поверхности медной подкладки, мкм; hсталь – микронеровность поверхности стали, мкм.

Величина микронеровностей поверхности свариваемого образца из листовой стали

12Х18Н10Т в состоянии поставки и медной подкладки определяли с помощью портативного измерителя шероховатости TR 100. Величина микронеровностей Ra на поверхности стали h Steel =0,54-0,72 мкм (для расчетов приняли 0,66 мкм), а на поверхности меди h Cu =2,1-3,61 мкм (приняли 2,90 мкм). Зависимость λ(T) воздуха принимали по данным работы [3]. Для вычисления коэффициента, учитывающего площадь фактического контакта стального образца и медной подкладки, воспользовались выражением, приведенным в справочнике [3]:

S ф =P/H              (6)

где P – давление на образец, кг/см2; H – твердость материала по Бринеллю, кг/см2 .

Для расчета этого коэффициента использовали экспериментально измеренное давление прижимов P=9,85 кг/см² и данные по твердости меди М1 из марочника [4]. В нашем случае получили для металлического контакта S ф =0,12, и поскольку эта величина относительно мала, то в соответствие с методикой [3], можно заключить, что термическая проводимость контакта приближенно может быть рассчитана только по значению α воз . Поскольку теплопроводность воздуха зависит от температуры, для расчета была использована линейная зависимость, полученная аппроксимацией табличных данных в программе STATISTICA в виде выражения:

α(Т)=10200+32Т         (7)

Эффективный КПД сварочной дуги определяли методом калориметрирования в стоячей воде по формуле:

_ ст А Т

^{П эф} = UIt_ce ’          (8)

св где c – теплоемкость воды, Дж/(кг·°С); m – масса воды, кг; ΔТ – перепад температур при калориметрировании, °С; U – напряжение на дуге, В; I – сила тока, А; tсв – время сварки, с. Режимы сварки образцов и полученные при этом значения эффективного КПД приведены в таблице 1.

Таблица 1. Данные по режимам сварки и коэффициенты модели

Режим	Сила тока, А	Скорость сварки, м/ч	Напряжение на дуге, В	КПД, %	Коэффициент сосредоточенности -2 дуги k, см
(а)	115	12	10,10	61	5,5
(б)	115	15	10,27	64	8
(в)	115	18	10,31	65	13

Сварка производилась на образцах из нержавеющей стали 12Х18Н10Т размерами 100х50х2 мм на стенде, приведенном на рис. 2. При сварке на всех режимах использовали вольфрамовые электроды WL-20 диаметром 3мм с углом заточки 30°, длина дуги 3 мм.

Рис. 2. Общий вид экспериментальной установки

Температурное поле определялось численным решением задачи нелинейной теплопроводности, пример расчета которой приведен на рис. 3.

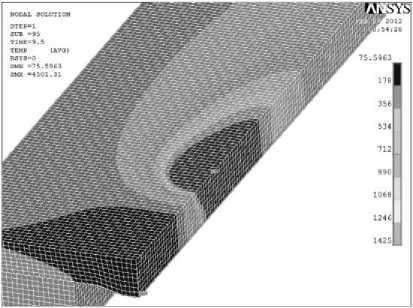
Рис. 3. Пример расчета в пакете ANSYS/ Multiphysics.

Мощность источников нагрева и коэффициент сосредоточенности дуги подбирались по следующему алгоритму – вначале по полуширине обратного валика подбиралась эффективная мощность линейного источника нагрева, после чего – по полуширине сварного шва выбирался коэффициент сосредоточенности дуги для нормально-кругового источника нагрева. В результате моделирования было установлено, что мощность линейного источника нагрева должна составлять 1/5 от общей мощности для того, чтобы ширина шва с лицевой и обратной стороны соответствовала экспериментальным данным.

Проверка расчетной методики определения проводимости теплового контакта осуществлялась путем записи термических циклов с термопар в медной подкладке, установленных в соответствии с рис. 4 и последующим их сравнением с термическими циклами узлов конечно-элементной сетки медной подкладки при расчете контактной тепловой задачи. При этом термопары типа «К» зачеканивали в медную пластину на глубину 1,5±0,5 мм и заливали термостойким герметиком.

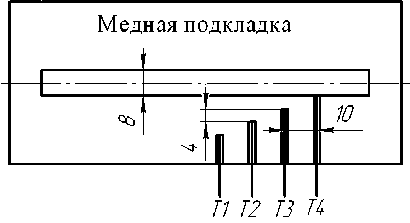
Рис. 4. Схема установки термопар в медную подкладку

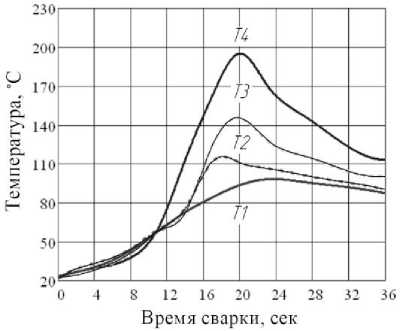
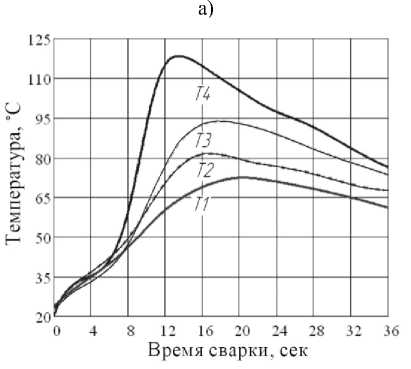
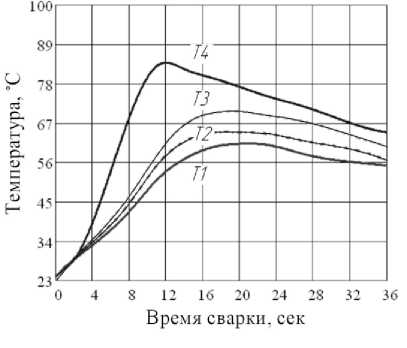
Термические циклы снимались с помощью цифрового 4-х канального измерителя температуры CENTER 309 . На рис. 5 представлены термические циклы режимов (а)-(в).

б)

в)

Рис. 5. Термические циклы режимов а)-в) в соответствии с таблицей 1.

В результате сопоставления экспериментальных термических циклов с расчетными, было установлено, что термическая проводимость, рассчитанная по теплопроводности воздушной прослойки между микронеровностями шероховатостей поверхностей, не отражает реальных условий сварки, по-видимому, в связи с отсутствием равномерного прилегания свариваемых деталей к медной подкладке. Поэтому в расчетной модели для определения значения αвоз необходимо использовать экспериментальный коэффициент, который в наших условиях составил 0,8.

Выводы:

• 1.    Для получения расчетной модели, адекватно описывающей влияние теплоотвода на ширину стыкового шва при аргонно-дуговой сварке на медной подкладке необходимо введение экспериментально полученных коэффициентов контактной теплопроводности между свариваемыми листами и подкладкой.

• 2.    Для аргонно-дуговой сварки стальных образцов толщиной 2 мм поправочный коэффициент к расчетному значению термической проводимости составил 0,8.