Определение волнового сопротивления колебательного контура квазирезонансного стабилизатора напряжения

В основу работы резонансных преобразователей напряжения (РПН) положено то, что реактивные элементы, такие как емкость и индуктивность, изменяют свой запас энергии с конечной скоростью. Следовательно, ток индуктивности и напряжение емкости не могут мгновенно изменить своего значения. При использовании в силовых цепях реактивных элементов, таких как дроссель и конденсатор (а при высоких частотах и паразитные реактивные элементы полупроводниковых приборов) можно добиться так называемого «мягкого» переключения силовых транзисторов при нулевых значениях тока или напряжения [1].

Одним из распространенных видов РПН является преобразователь последовательного типа с режимом коммутации ключевого элемента (КЭ) при нулевых значениях тока (ПНТ) (рис. 1). Основными достоинствами такого вида преобразователей являются: высокие значения КПД, низкий уровень пульсаций, малый уровень электромагнитных помех, уменьшение потерь на переключение КЭ, и, как следствие, снижение массы радиаторов [1]. Диаграммы сигналов в силовой цепи ПНТ-преобразователя, поясняющие его работу, показаны на рис. 2.

В связи с тем, что в одном периоде преобразования используется только часть резонансного цикла (рис. 2), такой тип ПН называют квазирезонансным. При всех преимуществах квазирезонансного ПНТ-преобразователя перед традиционными импульсными, с прямоугольной формой тока и напряжения, ему не удается их вытеснить из-за проблем, связанных с регулированием выходного напряжения. Это объясняется наличием нелинейной зависимости между эффективным значением тока дросселя выходного фильтра и средним значением напряжения на конденсаторе резонансного контура (РК) [2]. Функция, описывающая данную зависимость, может быть записа

на в следующем виде:

KU

U Cr

f ^ ⁽ I L ф

^K ( IL ф ) = —

2 п

п + arcsin

Z 0 IL ф

+ 0.5 ■

Z О IL ф

вх

, Z 0 IL ф '

1- U _ вх _

Z 0 IL ф

вх

,(1)

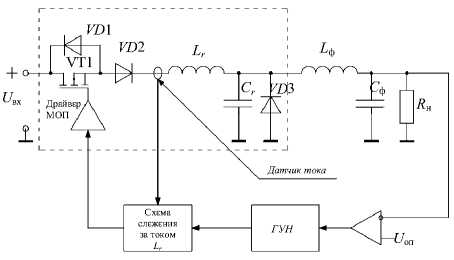
Рис. 1. Функциональная схема стабилизированного ПНТ-преобразователя: ГУН - генератор, управляемый напряжением, и_оп- опорное напряжение

где Z₀- волновое сопротивление РК, Т ^ ф - средний ток дросселя выходного фильтра, равный току нагрузки в установившемся режиме,,/к - частота коммутации,^ - собственная частота РК, Гц, С_вх - входное напряжение, Cr> - среднее значение напряжения емкости РКравное напряжению на нагрузке в установившемся режиме (без учета активных потерь в выходном фильтре), K- коэффициент передачи по напряжению ПНТ-преобразователя. График описанной выше зависимости представлен на рис. 3.

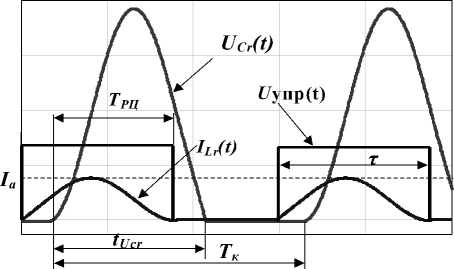
Рис. 2. Временные диаграммы работы ПНТ-преобразователя: Т _РЦ - время резонансного цикла

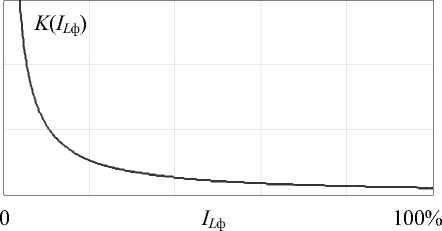
Рис. 3. Нелинейная зависимость коэффициента передачи ПНТ-преобразователя от тока нагрузки

Из-за наличия данной нелинейности регулирование (стабилизация) выходного напряжения при изменении тока нагрузки осуществляется за счет изменения частоты коммутации/,, вследствие чего изменяется Cr>. При работе в широком диапазоне токов нагрузки изменение / может достигать 50.. .60% от максимального значения, что обуславливает избыточность индуктивности дросселя выходного фильтра для работы, так как одним из усло-

вий режима переключения КЭ при нулевых значениях тока является AI_L <  21_Н Это, в свою очередь, приводит к снижению удельных характеристик преобразователя.

Параметры импульсов / , (/) и Ц.(/) (рис. 2) зависят, главным образом, от параметров РК, диапазон допустимых значений волнового сопротивления, Z₀ которого ограничен условием [3]

R <7 < U ^вх

^R Н min <  Z 0 <  i ,                  ⁽²⁾

где R^ - минимальное значение сопротивления нагрузки, 7_Ншах - максимальный ток нагрузки. Практические исследования показали, что изменение Z₀ внутри диапазона (2) при прочих определенных параметрах преобразователя существенным образом влияет на динамические и энергетические характеристики стабилизатора напряжения (СН), построенного на базе квазире-зонансного ПНТ-преобразователя. Степень влияния определяется диапазоном токов нагрузки, который ограничен по минимальному его значению в связи с принципиальными особенностями работы ПНТ-преобразователя. Таким образом, необходимость определения более точных значений параметров РК является актуальной задачей.

Для решения поставленной задачи энергетические и динамические характеристики силовой части СН могут быть описаны единым функционалом, анализ которого позволит определить наиболее рациональное значение Zo внутри установленного диапазона (2).

По результатам исследований, представленных в [1], КПД квазирезонансных ПНТ-преобразователей достаточно высок (более 90 %). Основные потери передаваемой мощности приходятся на КЭ, поэтому анализировать энергетические параметры целесообразно через мощность, рассеиваемую на КЭ, которая будет определяться эффективным значением тока, проходящего через него. Так как форма тока через индуктивность РК L близка к синусоидальной (рис. 2), его эффективное значение 1^ можно определить по формуле

L Г-П/. ^,                 (³)

D-T/T, где т - длительность импульса, соответствующая времени открытого состояния КЭ, T - период коммутации (рис. 2). Тогда значение мощности, рассеиваемой на КЭ, будет определяться формулой Р_КЭ =■ R_d, где R_d - активное сопротивление КЭ в открытом состоянии (в случае использования МОП-транзистора), которое при необходимости может включать в себя активное сопротивление индуктивности РК.

Подставляя в выражение (3) известную формулу для нахождения амплитудного значения тока I = 1_н + UJZ₀ получаем

P = (I + U^) ••

1 н Z0^ 2 • ТК    d.

Время открытого состояния КЭ определяется следующим выражением [4]:

, I .       1       .1        .I т = L —— +--,    +--arcsin ° r U^  nJL C to U^

DA       V Г Г       ОL DA

где U _вх - напряжение питания преобразователя; L_r C_r - индуктивность и емкость РК соответственно; Ю ₀ - собственная частота РК, рад/с;/0^- Ю ₀/2 л , Гц.

Период коммутации находится по следующей фор муле:

_т UK ( 1 _н) DA        Н

'Г вых f 0

Подставляя выражения (5) и (6) в выражение (4), получим формулу для мощности, рассеиваемой на КЭ. Значение мощности зависит от тока нагрузки, параметров РК и входного напряжения. Если считать, что входное напряжение изменяется незначительно, то мощность можно записать как функцию двух переменных:

п + arcsin вх

R d

P ( I н ^{, С} r ) =

U вх

^U вых

J ( I Н , С , ) + ^{1 +} У¹" ( J ⁽ I Н ^{, С} , ) ) ^:

,(7)

• п + arcsin ( J ( I _Н , С_r ) ) +

J ( I Н , С r )

1„и где J ( I н , Сr ) = ^Н .

to o • ^с r

Для дальнейшего анализа задаемся параметрами ква-зирезонансного СН, приведенными в таблице.

Параметры квазирезонансного СН

Параметр	/о, КГц	и вх, В	^ вых , В	Я„Ом	I - А Jнтт>	I    А Jнтах ,
Значение	750	60	20	0,028	1	5

График поверхности, отображающей зависимость (7), представлен на рис. 4.

I n

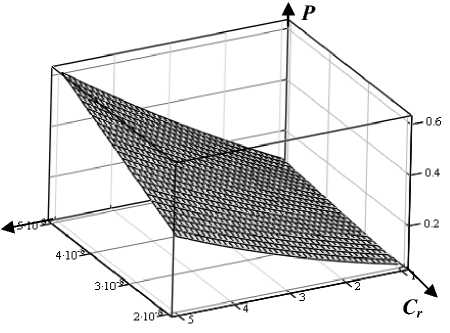
Рис. 4. Зависимость мощности, выделяемой на КЭ, от тока нагрузки и емкости конденсатора РК

Для объективной оценки недостаточно рассматривать только энергетический режим работы ПНТ-преобразователя, необходимо также учитывать и динамический режим данного СН. В качестве такого показателя может быть использована зависимость приращения частоты преобразования от С_г и 1_н при прочих заданных параметрах, которая является регулирующей переменной:

A F ( C r , I н ) =

fU

0 вых

U J KC ( I ) вх         Н

где^-ДТ , )-^).

График данной зависимости с начальными условиями из таблицы представлен на рис. 5.

Минимум значения мощности потерь на КЭ, в заданном диапазоне 1_н, будет соответствовать минимальной площади сечения S₁ фигуры, образованной поверхностью Р(С , 7) и плоскостями, ограничивающими диапазоны 1_н = [7_{н т} . _п , 7_нтах] и С_г. Диапазон С_г находится из условия (2), путем замены Z₀= 1/( ® ₀ * С):

U 1 U ВЫл                  Вл

I    " ^ ■ С_г ~1    ’

Нтах ⁰ r Нтах

II

Нтах ^ с ^ Нтах

U ⋅ ω U ⋅ ω

Вл 0             Выл 0

Минимум значения A F находится аналогично через соответствующую площадь сечения S₂, в обоих случаях площади S₁ и S₂ перпендикулярны оси С

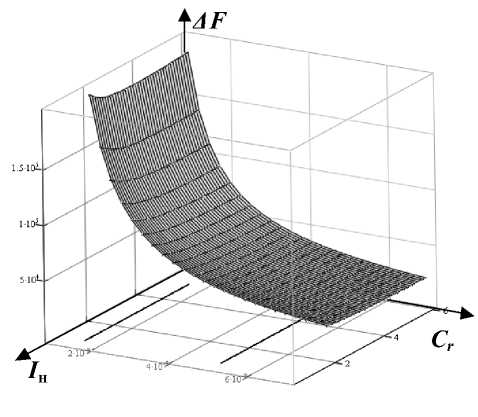
Рис. 5. Зависимость приращения частоты преобразования от С_г и 7 _н

Для комплексной оценки необходимо определять общий минимум функционалов Р(С_г, 7_н) и АТ(С., 7_н), соответствующий фиксированному значению С , в заданном диапазоне I, который можно найти, определив min (S₁ + S₂), что и будет соответствовать наиболее предпочтительному значению Z.

График суммы функций S^G) и S^G) (рис. 6), исходя из условия (9), ограничен по оси С_г. В данном случае нет экстремумов, это позволяет принять граничное значение емкости С_гтах внутри заданного диапазона при прочих определенных параметрах, по крайней мере, при тех исходных данных, которые были установлены для решения данной задачи.

Практика создания СН на базе ПНТ-преобразовате-лей, работающих в широком диапазоне токов нагрузки, показывает, что наилучшие удельные характеристики будут когда Z₀ >  Л_н, но в случае существенного увеличения ^_н по отношению к Z₀ величина/ к будет резко уменьшаться, что может привести к срыву резонансного процесса, поэтому при расчете такого рода СН накладываются жесткие ограничения на минимальное значения тока нагрузки.

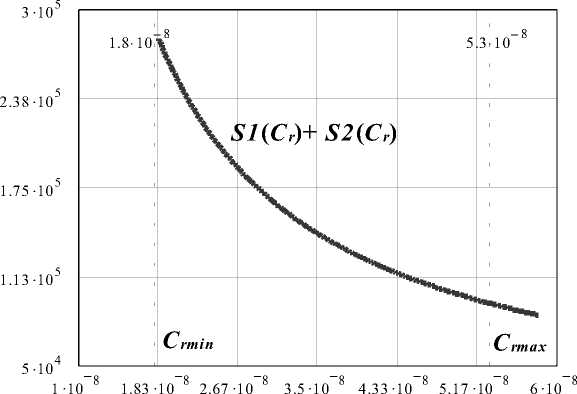
С г

Рис. 6. График суммы функций S^C) и S₂(С_r)

Таким образом, на основании предложенного анализа можно сделать вывод, что при работе в широком диапазоне токов нагрузки данного СН сопротивление волнового контура выбирается исходя из условия равенства минимальному сопротивлению нагрузки. Этот вывод подтверждается во всех случаях, где определенные прочие параметры силовой части квазирезонансного СН не противоречат основным режимам работы данного преобразователя.

Переходные процессы (ПП) на выходе СН на базе ПНТ-преобразователя без дополнительных корректирующих звеньев при набросе нагрузки приведены на рис. 7. Кривая 7 (рис. 7, а) соответствует Z₀ = ^_нт . _п= 3,92 Ом, кривая 2 (рис. 7, б) соответствует Z₀ = 7,07 Ом.

В случае ПП (рис. 7, а) колебательность и перерегулирование заметно ниже, чем в случае ПП (рис. 7, б), этот факт, в свою очередь, подтверждает правильность выбора волнового сопротивления РК в соответствии с выше-определенными критериями и ограничениями.

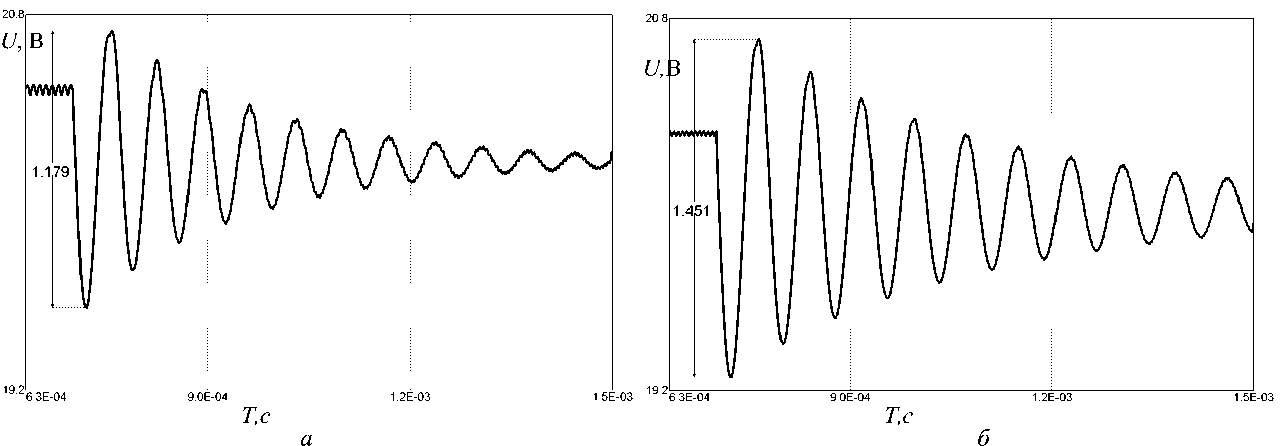
Рис. 7. Переходные процессы на выходе квазирезонансного СН при ступенчатом изменении нагрузки от 10до 3,9 Ом