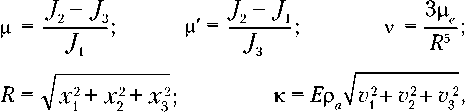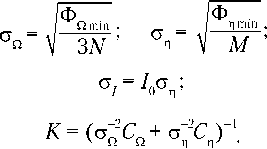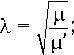Определение вращательного движения кораблей «Прогресс» по данным измерений угловой скорости и тока солнечных батарей

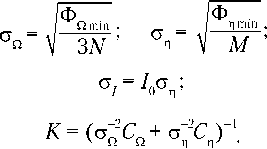
В первых двух формулах должно быть M ≫ 9; 3N ≫ 9. Стандартные отклонения определяемых параметров равны квадратным корням из соответствующих диагональных элементов матрицы K. Стандартные отклонения величин p_i, ω_i0, γ_b и т.п. будем обозначать σ_pi, σ_ωi, σ_γb.

Упрощенные способы обработки измерений

Движение ТГК в режиме закруток происходило с большой угловой скоростью, поэтому уравнения (1) и описанный выше способ обработки данных измерений целесообразно использовать только на относительно продолжительных отрезках времени. На коротких временных отрезках (30–40 мин) лучше использовать другие модели. В этих моделях движение ТГК и расчетные аналоги измерений описываются более простыми соотношениями, содержащими дополнительные уточняемые параметры, которые в соотношениях (1), (2), (3) считают-ся фиксированными — в рамках модели, при-веденной выше, они уточняются плохо.

Для описания зависимости от времени величин ω_i на сравнительно коротких отрезках времени оказалось возможным использовать динамические уравнения Эйлера свободного твердого тела, на которое не действуют внешние механические моменты. Эти уравнения имеют вид

(bj = ц<в2ю3;

■ ц'-ц .        , ох = 4-—-— охи,; со = - ц со, ох.

• ²  1 - ЦЦ’ ^{31   3}   ^12

  
  

Уравнения (5) допускают семейство стационарных решений:

ю1 = ®₃ = 0;    ®₂ = Q, (6)

где Ω — произвольная постоянная. Решения (6) описывают стационарные вращения ТГК вокруг его главной центральной оси максимального момента инерции. Движениям ТГК в режиме одноосной солнечной ориентации отвечают решения из малой окрестности семейства (6). Для нахождения таких решений можно воспользоваться линеаризованными уравнениями со^цОЮд; со3 = — n'OcOj; cb2=Q, решив которые, получим приближенные формулы общего решения уравнений (5):

cOj = X^sinv(t-1₀) + Bcosv(t- Q];

co9 = Q;

co, = v4cosv(t- t0) - Bsinv(f- f());

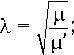
v = 07 ЛЛ'- где A и B — произвольные постоянные. Формулы (7) тем точнее, чем меньше абсолютные величины отношений A/Ω, B/Ω .

И решения (6), и формулы (7) можно использовать для обработки измерений угловой скорости ТГК, полученных во время реализации режима одноосной солнечной ориентации.

Расчетные аналоги измерений в обоих случаях определяются соотношениями (2). Рассмотрим сначала использование формул (7). В этом случае соотношения (2) содержат восемь параметров: A, B, Ω, λ, ν, γ, α и β, которые считаем независимыми и оцениваем методом наименьших квадратов из условия минимума введенного выше выражения Ф_Ω. После того как оценки указанных параметров найдены, вычисляем µ = λν/Ω; µ′ = ν/λΩ. Параметры µ, µ′ и углы γ, α, β характеризуют тензор инерции ТГК, поэтому представляют большой интерес. Более точные оценки этих параметров можно получить, минимизируя выражение Ф_Ωна решениях уравнений (5). В этом случае Ф_Ωрассматривается как функция другого набора из восьми параметров: ω_i0 = ω_i(t₀) (i = 1, 2, 3), µ, µ′, γ, α, β. Минимизация Ф_Ω в обоих случаях выполняется методом Гаусса– Ньютона. Сначала минимизация выполняется с использованием формул (7), ее результат служит первым приближением для минимизации Ф_Ωна решениях уравнений (5). Затем найденные параметры µ, µ′, γ, α, β используются при упрощенной обработке измерений тока и при минимизации функционала (4). Стандартные отклонения указанных параметров обозначим σ_µ, σ_µ′, σ_γ, σ_α, σ_β. Эти величины и стандартные отклонения остальных уточняемых параметров рассчитываются в рамках обычных предположений метода наименьших квадратов.

Упрощенная модель вращательного движения ТГК для обработки измерений тока СБ включает соотношения (2), (5) и уравнения Пуассона для компонент орта s в строительной системе координат. Эти компоненты обозначим s_i. В рамках вышеописанной модели они рассчитываются по формулам

• 5. = S.b, а., г = 1, 2, 3.

Если пренебречь изменением во времени величин Sk, то для компонент si будут справедливы уравнения st= s,,Q3-s3Q2; s2= s3Q,-s,Q3; s3= stQ2-s2Qr (8)

В этих уравнениях функции Ω_i = Ω_i(t) выражаются через решение уравнений (5) по формулам (2), параметры которых определены на заданном отрезке времени по измерениям угловой скорости ТГК. При этом значение η в формуле (3) расчетного аналога измеряемого тока принимается равным s₂.

Уравнения (8) интегрируются численно. Начальные условия компонент s_i выражаются через независимые параметры z₁и z₂по формулам 2z_t          1-_z2_ ₂2          2z₂

^Sc X^z^zX' ^S2”1+z=+z₂²’^S3^l”+^+4'

Это обеспечивает равенство 52+S2+ 53 = 1 в начальный момент времени. При численном интегрировании выписанное равенство выполняется с необходимой точностью в силу свойств уравнений (8).

Параметры z₁, z₂и максимальный ток I₀ находятся методом наименьших квадратов из условия минимума введенного выше выражения Ф_I на решениях системы (8). Начальные условия этой системы и системы (5), которая интегрируется совместно с уравнениями (8) для расчета функций Ω_i(t), задаются при f₀ = min(t_p /:'). Минимизация выполняется методом Гаусса–Ньютона из начальной точки z₁= z₂= 0; I₀= 29 А, отвечающей идеальной солнечной ориентации ТГК и номинальному значению максимального тока. Качество обработки характеризуется стандартными отклонениями искомых параметров σ_z1, σ_z2, σ_I0и стандартным отклонением ошибок измерений σ_I.

Результаты упрощенной обработки измерений

Некоторые результаты обработки измерений угловой скорости приведены на рис. 1 и в табл. 1. В табл. 1 использовано декретное московское время — ДМВ (UTC + 3 ч). В ней для каждого интервала измерений указаны: его номер, начальная точка t₁, длина t_N – t₁и N — число включенных в обработку моментов времени с измерениями. Интервалы 1–6 относятся к полету ТГК «Прогресс М-13М», измерения на интервалах 7, 8 получены в ходе полета ТГК «Прогресс М-14М». Интервал 6 включает интервалы 4, 5. Табл. 1 также содержит результаты обработки измерений с использованием решений системы (5) (обработка с использованием формул (7) дает близкие результаты). Во всех случаях в качестве момента t₀использовался момент t₁. В табл. 1 указаны оценки параметров и их стандартные отклонения; единицами измерения углов и угловой скорости служат, соответственно, радианы и 10^–3c^–1 (при такой единице времени орбитальная частота равна 1,14). Как видно из табл. 1, упрощенная обработка измерений угловой скорости позволяет получить приемлемые оценки тензора инерции ТГК. Особенно интересна оценка угла γ ≈ 7°. Это соотношение выполняется и для ТГК «Прогресс М-11М». Согласно формулам (2), (7), именно угол γ определяет возмущенное движение ТГК в режиме закрутки на Солнце при принятом способе построения начальных условий режима.

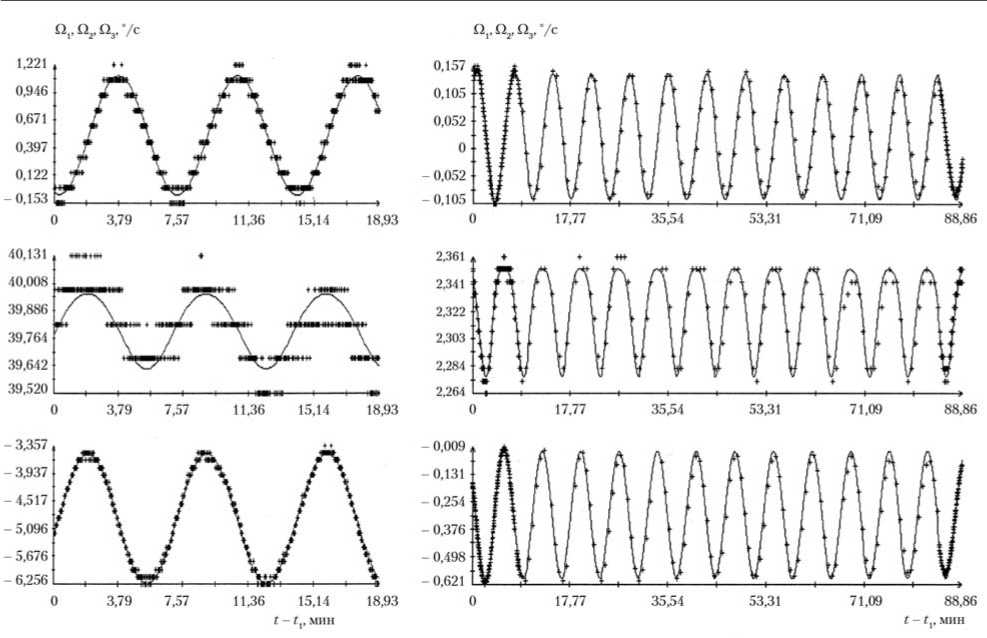
Рис. 1. Обработанные данные измерений угловой скорости: маркеры — данные измерений; сплошные кривые — графики аппроксимирующих решений системы (5); слева — интервал 2; справа — интервал 8 (табл. 1)

Таблица 1

Результаты упрощенной обработки измерений угловой скорости

Продолжение таблицы 1

Графики реконструированных функций Ω_i(t) (i = 1, 2, 3) на двух обработанных интервалах изображены сплошными линиями на рис. 1. Маркеры рядом с графиками указывают данные измерений — точки (t_n, ci"'). Согласно данным в табл. 1, характерное среднеквадратичное значение ошибки аппроксимации измерений угловой скорости составляет σ_Ω = 10^–4с^–1 ≈ 0,006 °/с.

Результаты упрощенной обработки измерений тока приведены на рис. 2. и в табл. 2. Таблица содержит номера интервалов измерений (цифры со штрихом), их начальные точки ^1 , длины 41 ^ и M — число включенных в обработку моментов времени с измерениями.

Кроме того, для каждого интервала с измерениями тока в таблице указан номер интервала с измерениями угловой скорости, результаты обработки которого использованы в соответствующей системе (8), и результаты минимизации функционала Ф_I: оценки параметров упрощенной модели, их стандартные отклонения, стандартные отклонения ошибок измерений σ_I и величины σ_η, ^0 /^ . Номер интервала с измерениями угловой скорости указывает, в частности, на использованные значения параметров µ, µ′, γ, α, β из табл. 1. Эти значения индивидуальны для каждого обработанного интервала.

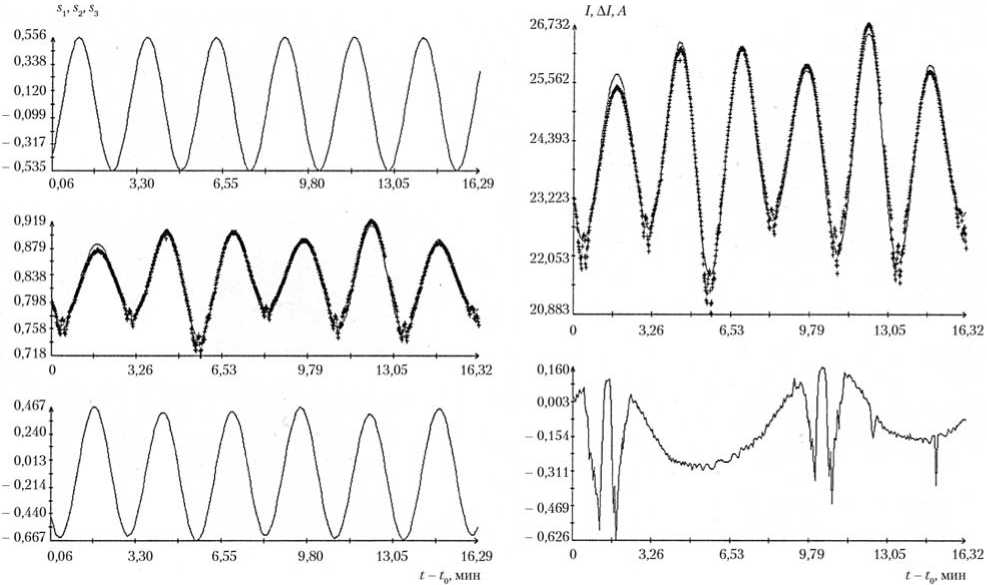
Рис. 2. Обработанные данные измерений тока на ТГК «Прогресс М-13М» (интервал 2′): маркеры — данные измерений; сплошные кривые — графики аппроксимирующих функций; t₀= 11:32:19 ДМВ 31.10.2011

Таблица 2

Результаты упрощенной обработки измерений тока

Интервалы 1'-6' относятся к полету ТГК «Прогресс М-13М», интервалы 7', 8' — к полету ТГК «Прогресс М-14М». Интервалы 1'-3' короткие, у них левые (правые) концы отрезков [t1, tN] и [tp ^] отстоят друг от друга на несколько минут. На рис. 2, иллюстрирующем интервал 2', сплошными гладкими линиями изображены графики решения системы (8) — функций s_i(t) (i = 1, 2, 3), а также график расчетного аналога тока СБ — функции I = I₀s₂(t). Графики построены на отрезке

. Маркеры рядом с графиками s₂(t) и I(t) — точки и , где m = 1, 2, ..., M. Нижний правый график на рисунке — ломаная с вершинами в точках . Эта ломаная иллюстрирует ошибку аппроксимации измерений тока упрощенной моделью.

Судя по рис. 2 и значениям стI в табл. 2, аппроксимация измерений тока на коротких интервалах получилась достаточно точной. Однако для более продолжительных интервалов 4'-8' описанный способ обработки оказался неудовлетворительным. Поскольку уравнения (5) и даже формулы (7) вполне приемлемы для описания изменения угловой скорости ТГК, уравнения (8) должны достаточно точно описывать изменение компонент орта s в строительной системе координат. Уравнения (8) имеют простую структуру. Это линейные дифференциальные уравнения с периодическими коэффициентами (все представляющие интерес решения системы (5) — периодические). Система (8) имеет кососимметрическую матрицу, поэтому ее матрица монодромии ортогональна. Один мультипликатор системы (8) равен 1, два других образуют пару комплексносопряженных чисел, лежащих на единичной окружности. По этой причине в случае найденных Qi(t) любое решение системы (8) для переменной s2 имеет специфический вид и совсем не похоже на любой из верхних осциллирующих графиков на рис. 3. Указанные графики — это ломаные с вершинами в точках , где m = 1, 2, ..., M. Они должны быть близки графикам функций I0s2(t) и не могут содержать ярко выраженной низкочастотной (с частотами менее 0,001 Гц) составляющей, которая в них очевидно присутствует. Такая составляющая не имеет отношения к движению ТГК и из обрабатываемых измерений тока должна быть исключена.

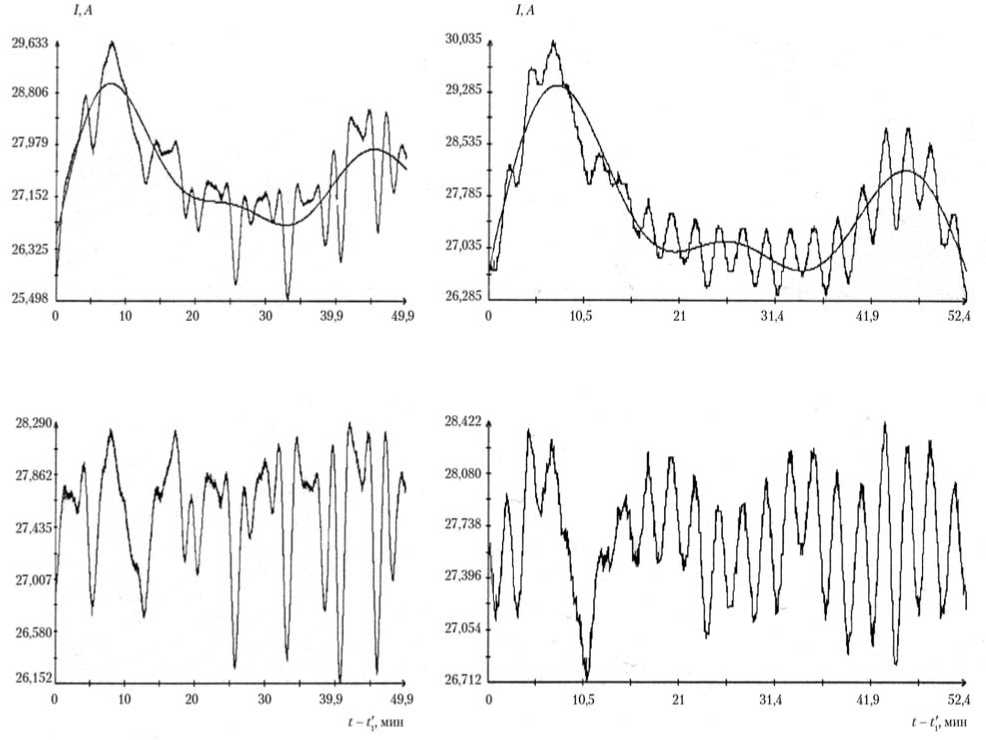
Рис. 3. Скорректированные данные измерений тока: слева — интервал 6 ; справа — интервал 7 ; вверху — исходные данные и корректирующая функция; внизу — скорректированные данные (значения указаны в табл. 2)

По-видимому, эта составляющая обусловлена вкладом солнечного света, отраженного от поверхности Земли. Математическая модель указанной составляющей еще не реализована в описываемом программном комплексе реконструкции вращательного движения ТГК, поэтому исключение данной низкочастотной составляющей из измерений тока на интервалах 4′–8′ выполнялось формальным способом.

Способ состоит в следующем. Сначала строится аппроксимация низкочастотной составляющей с помощью выражения (конечного ряда Фурье)

l        πl(t - t₁′)

χ(t) = a_L+1+ a_L+2(t - t₁′) + ∑ a_l sin            ^,

I =1         t_M t₁

коэффициенты которого a1, a2, ..., aL+2 наилучшим образом (при использовании метода наименьших квадратов) сглаживают точки , m = 1, 2, ..., M. Графики низкочастотной составляющей для интервалов 6′, 8′ изображены плавными линиями в верхней части рис. 3. Затем вычисляется среднее значение 〈χ〉 выражения χ(t) на сетке . Функция χ(t) – 〈χ〉 считается той посторонней составляющей, которую следует удалить из данных измерений. Удаление состоит в замене величин Im величинами Im – χ (tm) + 〈χ〉 с сохранением прежних обозначений. Ломаные линии, проходящие через новые точки , приведены в нижней части рис. 3.

Результаты обработки скорректированных измерений тока на интервалах 4′–8′ приведены в соответствующих строках табл. 2. Рис. 4–6 составлены аналогично рис. 1, 2 и иллюстрируют эти результаты для интервалов 6′ и 7′. На рис. 4, 5 сплошными гладкими линиями изображены графики функций Ω_i(t) и s_i(t) (i = 1, 2, 3) — коэффициентов и решений системы (8). Графики Ω_i(t) построены на отрезке [t₁, t_N] , графики s_i(t) — на отрезке

. Маркеры рядом с графиками Ωi(t) — это использованные для построения решений системы (5) измерения ' tn,£inn)), n = 1, 2,..., N; маркеры рядом с графиками s2(t) — точки , m = 1, 2, ..., M. В верхней части рис. 6 приведены результаты аппроксимации измерений функциями I = I0s2(t), а в нижней части рисунка представлены ошибки такой аппроксимации. Как видим, ошибки аппроксимации скорректированных измерений тока их расчетным аналогом на интервалах 6′, 7′ несколько выше, чем в случае интервала 2′. Расчетный аналог плохо воспроизводит некоторые локальные детали измерений, хотя значения σI остаются примерно на прежнем уровне. Следовательно, коррекция сделана не вполне адекватно, однако без нее согласие измерений с моделью было бы значительно хуже.

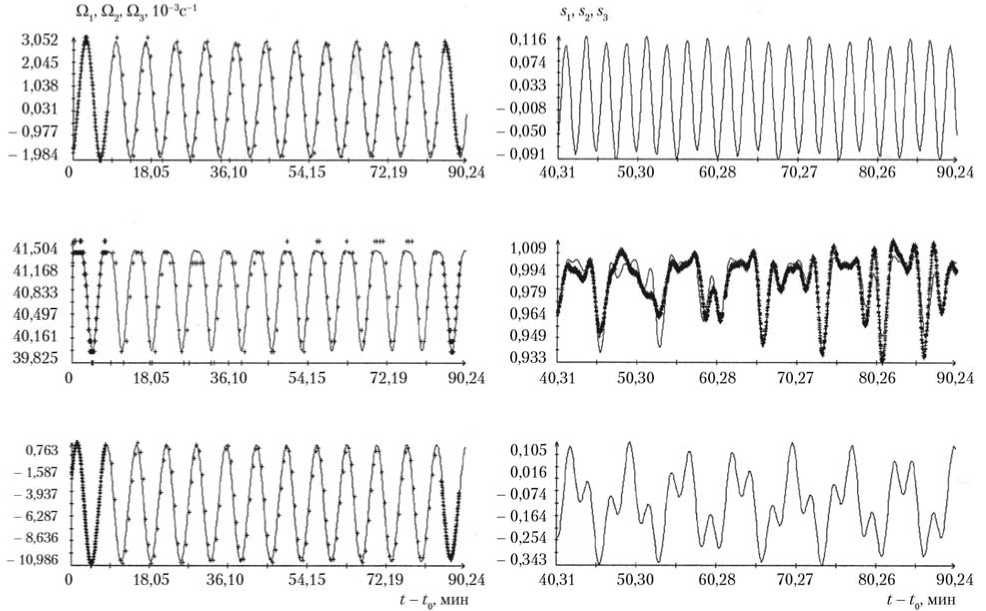
Рис. 4. Обработанные данные измерений угловой скорости и тока на ТГК «Прогресс М-13М» (интервалы 6 и 6′): маркеры — данные измерений; сплошные кривые — графики аппроксимирующих функций; = 16:09:45 ДМВ 01.11.2011

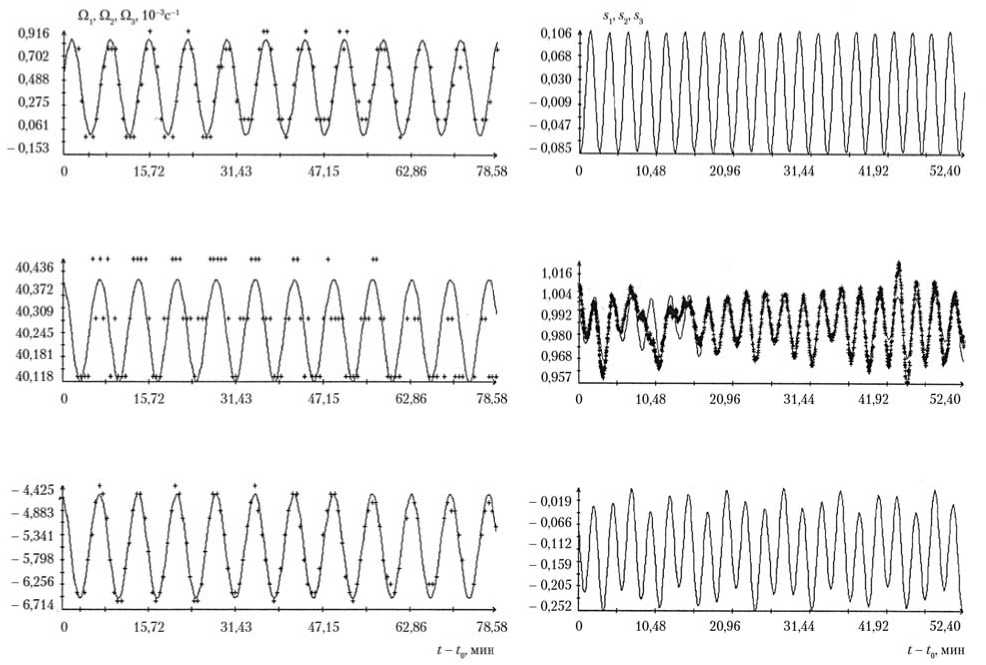
Рис. 5. Обработанные данные измерений угловой скорости и тока на ТГК «Прогресс М-14М» (интервалы 7 и 7′): маркеры — данные измерений; сплошные кривые — графики аппроксимирующих функций; t₀= 21:42:31 ДМВ 26.01.2012

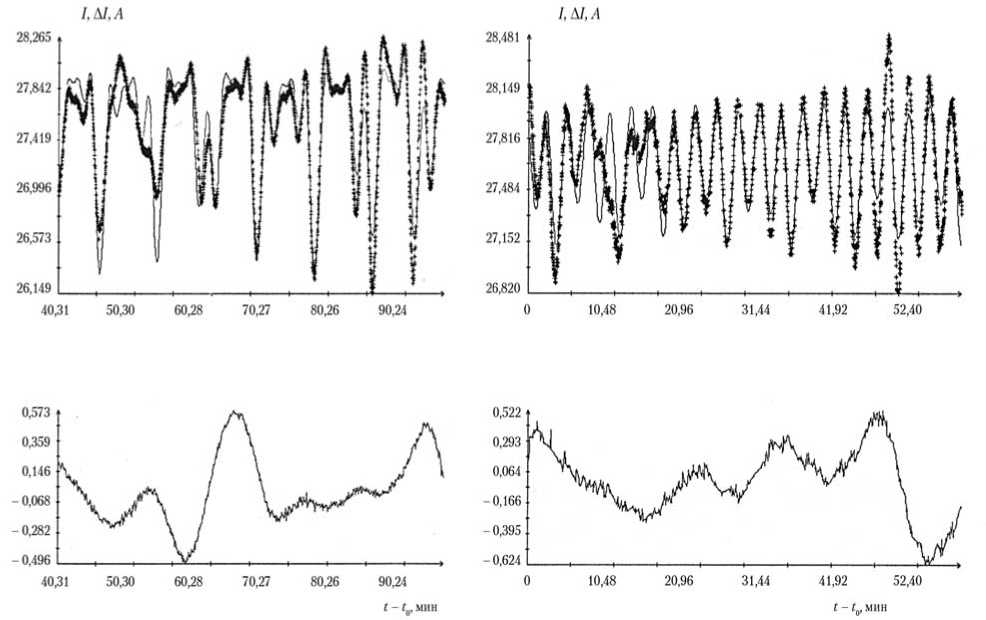
Рис. 6. Аппроксимация измерений тока на интервалах 6 (t₀= 16:09:35 ДМВ 01.11.2011) и 7 (t₀= 21:42:31 ДМВ 26.01.2012) с помощью упрощенной модели: маркеры — данные измерений; сплошные кривые — графики аппроксимирующих функций

Результаты обработки измерений с помощью полной модели

Обработка измерений с помощью полной модели была выполнена на пяти интервалах времени. Результаты обработки представлены в табл. 3 и на рис. 7, 8. Состав измерений на этих интервалах соответствует интервалам 4′–8′ из табл. 2.

В случае интервалов 6′, 7′ и 8′ соответствие полное, в случае интервалов 4′ и 5′ данные измерений угловой скорости несколько дополнены. Вследствие указанного соответствия обозначения интервалов в табл. 2 и 3 одинаковы. В частности, включенные в обработку интервалы измерений угловой скорости из табл. 1 указаны в скобках в первом столбце табл. 3.

Таблица 3

Результаты упрощенной обработки измерений угловой скорости

Продолжение таблицы 3

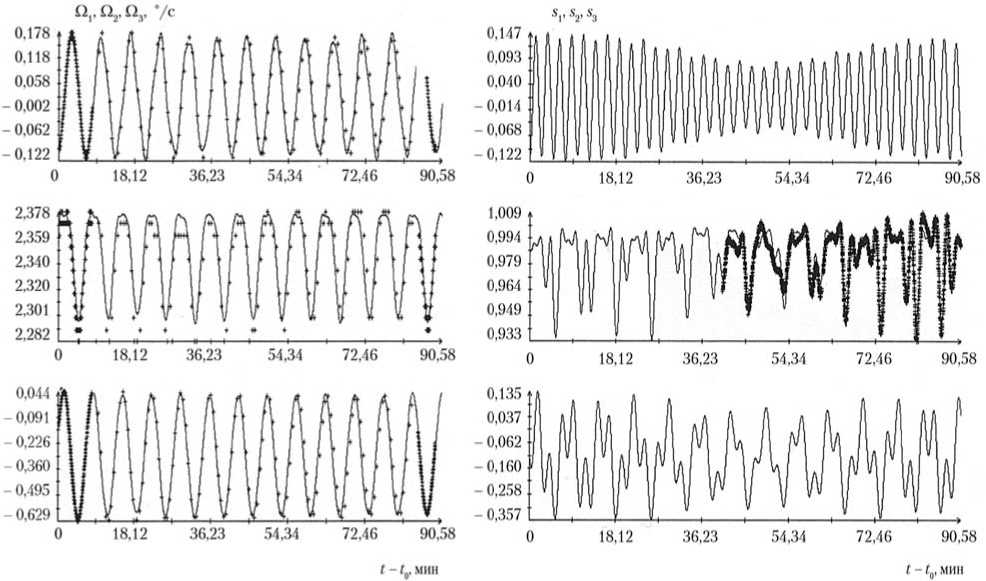
Рис. 7. Обработанные данные измерений угловой скорости и тока на ТГК «Прогресс М-13М» (интервалы 6 и 6′) с помощью полной модели: маркеры — данные измерений; сплошные кривые — графики аппроксимирующих функций; t₀= 16:09:35 ДМВ 01.11.2011

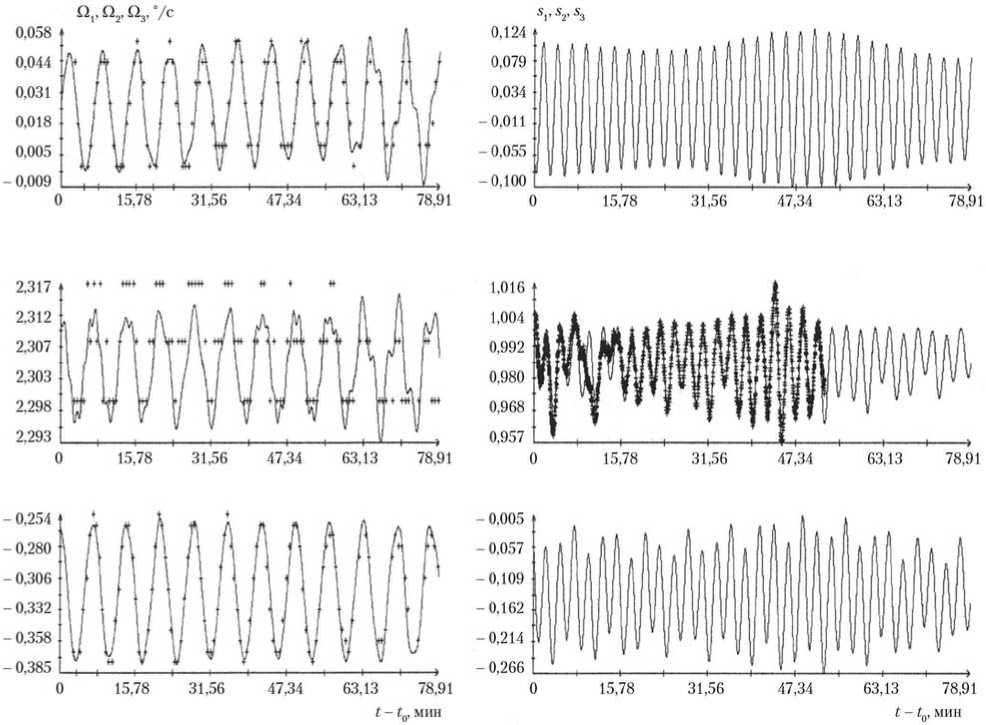
Рис. 8. Обработанные данные измерений угловой скорости и тока на ТГК «Прогресс М-14М» (интервалы 7 и 7′) с помощью полной модели: маркеры — данные измерений; сплошные кривые — графики аппроксимирующих функций; t₀= 21:42:21 ДМВ 26.01.2012

Обработка выполнялась в два этапа. На первом этапе минимизировался функционал наименьших квадратов , в котором отношение бралось из соответствующей обрабатываемому интервалу строки табл. 2. Начальная точка минимизации формировалась следующим образом. Значения углов γ_b, δ_b и β_b находились из условия, что ось 0x2 направлена точно по орту s, а ось 0x 1 лежит в плоскости CY₁Y₂. Начальные условия угловых скоростей, I₀и параметры тензора инерции ТГК выбирались такие же, как при упрощенной обработке соответствующих интервалов из табл. 2. Принималось p₁= p₂= p₃= 0. Минимизация Ф₃выполнялась сначала методом Левенберга–Марквардта, а после окончания его работы полученный результат проверялся методом Гаусса–Ньютона. Затем минимизировался функционал (4).

Как оказалось, решение системы (1), обеспечивающее локальный минимум функционалу (4) или Ф3, не единственное. После того как один локальный минимум найден, преобразование углов γb → –γb; δb → δb ±π; βb → –βb позволяет иногда получить из най- денной точки минимума начальное приближение для удачного поиска другого локального минимума с весьма близким значением функционала. Это преобразование задает поворот ТГК вокруг оси 0x2 на угол π. В указанном выше начальном приближении точки экстремума ось 0x1 в плоскости орбиты можно направить двумя способами. Разные направления этой оси также могут привести к разным точкам минимума.

Аппроксимация данных измерений разными решениями системы (1), обеспечивающими функционалу (4) близкие минимальные значения, на вид одинакова; количественно (по значениям σΩ и ση) такие аппроксимации почти идентичны. В такой ситуации для выбора решения, описывающего фактическое движение ТГК, необходимо привлечение дополнительной информации о положении осей ТГК. Если же не задаваться целью детальной реконструкции движения, а сосредоточиться на свойствах солнечной ориентации, то можно ограничиться анализом движения орта s в строительной системе координат ТГК. Конкурирующие минимали функционала (4) описывают его практически одинаково. По этой причине на рис. 7, 8 движение ТГК иллюстрируется графиками компонент угловой скорости Ωi(t) и компонент орта s в системе 0y1y2y3. Графики изображены сплошными линиями. Маркеры на рисунках указывают точки (tn, ci'") и ^/rz^m^ .

В табл. 3 приведены оценки уточняемых параметров полной модели, их стандартные отклонения, а также стандартные отклонения ошибок измерений σ_Ω и σ_η. Кроме того, в таблице приведены моменты времени t₀, в которые задавались начальные условия системы (1) и длины Δt объединенных интервалов [^.rJU^.rJ. Анализ таблиц и рисунков показывает, что результаты обработки измерений с помощью полной модели несколько изменились по сравнению с результатами упрощенной модели, но все же близки последним.

Выводы

Таким образом, с помощью данной методики можно рассчитать фактическое движение ТГК и квазистатическое микроускорение в любой заданной точке его борта. Указанная неединственость реконструкции движения практически не повлияет на результат.

Полученные результаты позволяют рационально планировать эксперименты в области микрогравитации на ТГК «Прогресс» и рассчитывать квазистатические микроускорения, возникающие при их проведении.