Определение закона и параметров регулирования инерционного вибропривода зерноочистительной машины

Около 57 % исследований виброобработки материалов и сред в АПК приходится на вибросепарацию семян, при этом в вибромашинах (ВМ) наибольшее применение нашли инерционные вибраторы, доля которых в виброзерноочистительных машинах (ВЗМ) составляет 85 %.

Согласно технологическим требованиям к сепарации семян различных сельскохозяйственных культур, для семян каждой культуры необходимо обеспечить изменение амплитуды колебаний рабочего органа (РО) А от частоты ю₂ внутри рабочей зоны по гиперболическому закону [1]:

А = Р7со₂, (1) где V - скоростной фактор, имеющий свое значение для каждого типа ВЗМ.

Наиболее эффективным для сепарации и транспортировки семян являются винтовые колебания рабочего органа ВМ. С этой точки зрения перспективной машиной считается многорешетная ВЗМ (МВЗМ) с саморегулируемым двухвальным вибратором [2]. Двухвальный вибратор имеет 8 дебалансов, установленных консольно, с углом первоначальной установки а относительно горизонтальной оси, попарно противоположно друг другу. При этом один из дебалансов неподвижен, а второй поджат фасонной пружиной с жесткостью К(р).

В этом случае амплитуда колебаний РО с массой т, и моментом инерции f относительно вер тикальной оси, с определенным радиусом R решета имеет следующий вид:

Я = ^hH —^£2 Jsin² a + m²a²R²J? cos² а, (2) т,                         "

где т_х и Г] - масса и радиус центра масс неподвижных дебалансов; т_г и р - масса и радиус центра масс выдвигающихся дебалансов; а - расстояние от вертикальной оси до плоскости вращения дебалансов.

Решая совместно (1) и (2), можно получить закон изменения радиуса центра массы т₂ подвижного дебаланса:

р =1 - Ю т2  4m2f sin2 a+ (mtaRJz] cosa)2 ю2

Подставляя (2) и (3) в уравнение равенства упругой силы пружины и центробежных сил дебалансов F_y = Р_ц или 7^(р)[р + (в-г₀)] = т₂р и выразив их через ю₂, получим характеристику жесткости, противодействующей выдвижению подвижного дебаланса, фасонной пружины саморегулируемого вибратора:

.          m2m2J2V2

^(р) =---5---2 ------ 3— ^х

16(Л sin а + т;а R cos^-а)

[р + Се-ГоЖ^г, -т2Р)2 ’

Возмилов А.Г., Яруллин Р.Б.

Определение закона и параметров регулирования инерционного вибропривода зерноочистительной машины где е - предварительная деформация фасонной пружины; г0 - радиус центра масс подвижного дебаланса в состоянии покоя.

Как известно, главной характеристикой упругих элементов служит функциональная зависимость между приложенной силой F и деформацией. Учитывая, что F = КМ и А^-в=р—г₀, упругая сила определяется из выражения:

_ ^JTV² р

*                   3         7 7 7     7                        7 *    '

16(7. sin a + m_ta R cos а) (т^^-т^рГ

Аналогично можно определить параметры саморегулируемого вибратора для любого типа ВМ. Расчеты по полученным выражениям были проведены для МВЗМ с параметрами (рис. 1): т, = 372кг;7. = 48,68кгм ²; т_х= 2,8кг; т₂= 2,2кг; г₀ = 0,005 м ;г_х= 0,11047 м; К = 0,268 м/с; a = 68³;

/? = 0,475м;а = 0,175м;е = 0,005 м.

На основании анализа влияния конструктивно-кинематических параметров МВЗМ на характеристики саморегулируемого вибратора была разработана методика расчета данного вибратора.

Скоростной фактор, диапазоны регулирования по частоте и амплитуде колебания РО определяются исходя из рациональных режимов работы ВМ для соответствующей отрасли [1].

По граничным значениям диапазона изменения амплитуды колебаний, исходя из известных конструктивных параметров ВМ, рассчитываются эквивалентные значения статических моментов масс дебалансов вибратора для крайних положений дебаланса по выражению:

мак               .        тл

/   \МИН      .        *

(щг)экв — /1мак — мин , кгм ,      (6)

мин   С     мак

С®2

где Л^ - граничные значения диапазона регули рования амплитуды колебаний РО, м; с - безразмерный коэффициент, учитывающий конструктивно-кинематическую особенность ВМ, определяемый для ВЗМ по работе [2]. Для МВЗМ он равен с = Jsin2 a. + m2a2R2J~2 cos2 a ; o)^ - граничные значения диапазона регулирования угловой частоты колебаний РО, рад/с.

Далее определяются параметры дебалансов. При этом из конструктивных соображений необходимо выполнение условия рмак < гх, а значения г0, гь тх и т2 принимаются по возможности минимальными.

Радиус центра массы ij неподвижного дебаланса mi равен

^ЧО^+^ьР^цМ. (7)

Максимальный радиус р подвижного дебаланса т_г равен

После определения основных параметров дебалансов рассчитывается характеристика упругой силы F нелинейной пружины саморегулируемого вибратора МВЗМ по выражению (5).

Для технологической простоты изготовления нелинейной пружины предлагается путем кусочнолинейной аппроксимации характеристики упругой силы заменить фасонную пружину несколькими линейными пружинами, установленными с определенными первоначальными зазорами Ак, которые вытекают в результате аппроксимации (рис. 2).

Параметры фасонной пружины также можно рассчитать по программе КОМПАС 3DV7 (приложение КОМПАС-Spring).

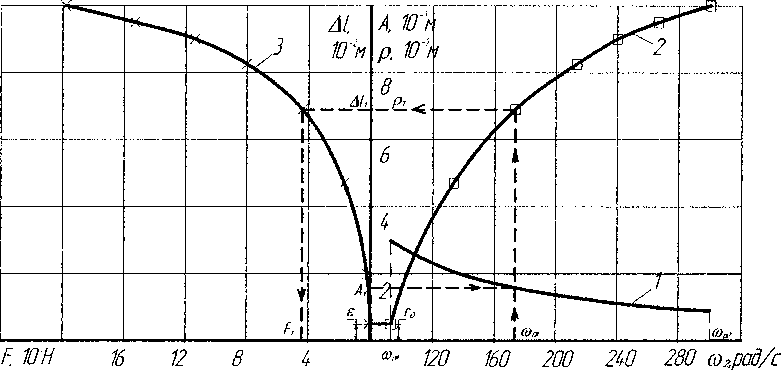
Рис. 1. Амплитудно-частотная и силовая характеристики саморегулируемого вибратора многорешетной виброзерноочистительной машины: 1 - зависимость амплитуды колебаний рабочего органа A=f (ш₂); 2 - зависимость радиуса центра массы подвижного дебаланса р=^ш₂); 3 - зависимость упругой силы фасонной пружины Е=А.Ы')

Электромеханика

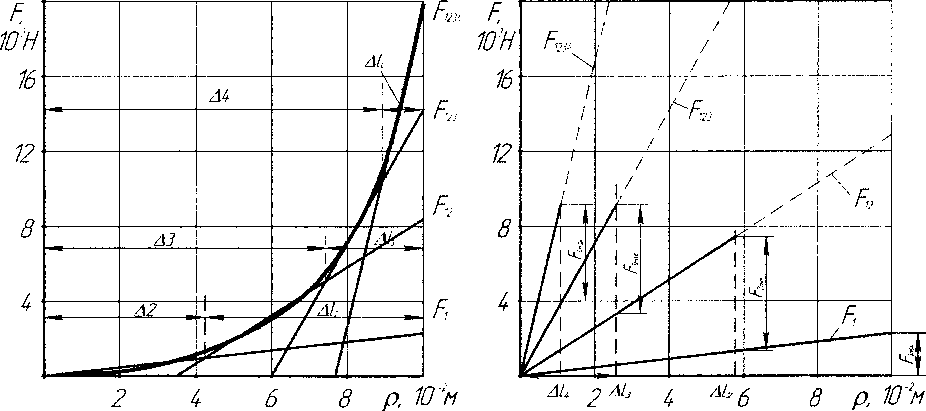
Рис. 2. Кусочно-линейная аппроксимация характеристики упругой силы фасонной пружины четырьмя линейными пружинами F^, Рг, F^, F4

Выводы

• 1.    Определен закон и параметры регулирования кинематического режима инерционного вибропривода зерноочистительной машины.

• 2.    Разработана методика расчета основных параметров инерционного саморегулируемого вибратора.