Определение запаса усталостной прочности в конструкции стрясной доски комбайна КЗС-1119Р

Введение. Разработка образцов новой техники в области машиностроения, удовлетворяющих самым современным требованиям, связана с всесторонними исследованиями прочности и жесткости несущих конструкций с учетом рабочих и экстремальных нагрузок, возникающих при эксплуатации, а также с учетом воздействия внешней среды. Экспериментальное проведение таких исследований связано, как правило, со значительными затратами временных и материальных ресурсов. Поэтому применение высокоэффективных и точных методов расчетных исследований является основой для создания надежной и конкурентоспособной техники.

Одним из таких методов является метод конечных элементов - в настоящее время основной инструмент решения задач строительной механики, механики деформируемого твердого тела. Для МКЭ характерны широкий диапазон применимости, инвариантность по отношению к геометрии конструкции и механическим характеристикам материалов, высокая степень приспособленности к автоматизации всех этапов расчета [1,2].

Рама сельскохозяйственной машины - это прежде всего сварная конструкция с наличием значительного числа концентраторов напряжений в виде отверстий различной конфигурации, резкого изменения геометрической формы и размеров, а также собственно сварных швов, являющихся серьезным источником местных напряжений, поскольку для них характерна неоднородность материала шва, наличие всевозможных дефектов и остаточных напряжений, обусловленных температурными деформациями. Напряженность рамной конструкции изменяется во времени, что требует проведения расчетов прочности конструкций по критериям сопротивления усталости [1, 5, 6, 8, 9,10].

Постановка задачи. Расчет выполнен при динамическом нагружении стрясной доски в процессе работы системы очистки зерноуборочного комбайна. Задача заключается в том, чтобы рассчитать непрерывное изменение полей главных напряжений за один цикл движения стрясной доски и определить зоны с максимальным изменением этих напряжений [2]. Расчет проведен с учетом демпфирования конструкции. Согласно [4] коэффициент демпфирования для металлической конструкции изменяется в диапазоне 0,020,04, для расчета принят 0,025. Для прочностного анализа механизма привода очистки со стрясной доской приняты следующие характеристики сайлентблоков: радиальная жесткость Fr=17600 Н/мм, осевая жесткость Ғд=2500 Н/мм, крутильная жесткость Скр=11000 Н/мм, демпфирующие коэффициенты для резины приняты 10% от заданных жесткостей согласно [7].

Для сокращения времени расчета с учетом симметричности конструкции стрясной доски рассматривалась только ее половина. Для выполнения расчета смоделирован привод, обеспечивающий движение стрясной доски при частоте вращения приводного вала 277 об/мин.

Расчетная схема нагружения конструкции стрясной доски показана на рисунке 1.

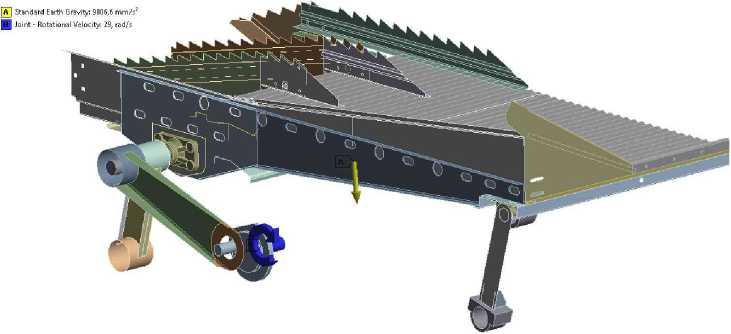
Рисунок 1 - Расчетная схема нагружения конструкции

Результаты исследования. Основными дифференциальными уравнениями движения, решае мыми неявным переходным динамическим анализом согласно [3], являются:

d2x    dx .     „ т—т + с---v k • х = г t , dr    dt

где m - матрица масс;

• с - матрица коэффициентов радиального или осевого демпфирования конструкции;

• к - матрица коэффициентов радиальной или осевой жесткости конструкции;

• х- обобщенная координата системы;

F(t) - вектор нагрузок.

Т d^ф , dф , , „ ,          _

J ■ —— + Һ ---ғ d • ф — М t ,    (2)

dt1 dt где J - матрица моментов инерции;

• Һ - матрица коэффициентов крутильного демпфирования конструкции;

• d - матрица коэффициентов крутильной жесткости конструкции;

• Ф - обобщенная координата системы;

M(t) - вектор моментов.

В любой момент времени t уравнения (1) и (2) можно рассматривать как набор «статических» уравнений равновесия, которые также учитывают силы инерции и силы затухания. Для решения этих уравнений в дискретных временных точках используется метод интеграции времени. Приращение времени между последовательными временными точками называется шагом времени интегрирования.

Матрица масс элементов конструкции стрясной доски, а также матрица моментов инерции вращающихся масс определяется исходя из геометрии ее элементов.

Матрица затухания [С] вычисляется с использованием констант а и /3 и произведения этих констант на матрицы масс [М] и матрицы жесткости [К] соответственно [5]:

• [С] = сг-М + №]. (3)

Коэффициент демпфирования /3 представляет собой отношение коэффициента модального затухания к круговой частоте свободных колебаний [6].

^-^, (4) wz где е, - коэффициент модального затухания:

W, - круговая частота свободных колебаний;

Коэффициент модального затухания с представляет собой отношение фактического демпфирования к критическому затуханию для конкретного режима колебаний [8].

Результаты расчета. Цикл перемены напряжений в элементах конструкции стрясной доски связан с формой ее движения - возвратно-поступательное плоскопараллельное движение с перемеще нием доски вперед-вниз и назад-вверх. При этом экстремумы главных напряжений по результатам предварительных расчетов наблюдаются в крайних точках траектории.

На рисунках 2 и 3 изображены наиболее нагруженные по результатам расчета зоны конструкции: борт стрясной доски в околошовной зоне пробкового шва приварки усилителя (зона А) и передняя ось подвески стрясной доски (зона Б).

На рисунке 2 изображены поля главных максимальных напряжений в конструкции стрясной доски:

• -    в зоне А максимальные главные напряжения (рисунок 2) стах =+52,3 МПа;

• -    в зоне Б максимальные главные напряжения (рисунок 2) Стах =+101,7 МПа.

На рисунке 3 изображены поля главных минимальных напряжений в конструкции стрясной доски.

• -    в зоне А минимальные главные напряжения (рисунок 3) Omin = -2,91 МПа;

• -    в зоне Б минимальные главные напряжения (рисунок 3) Cmin = -93,4 МПа.

  

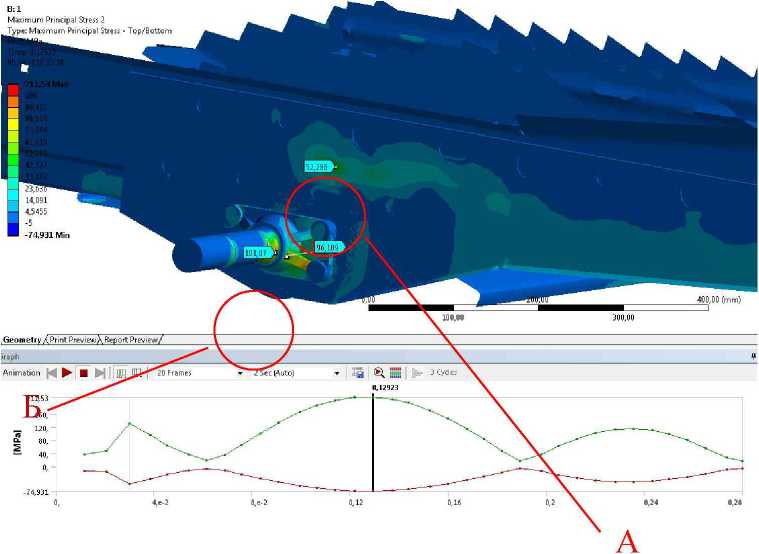
  Рисунок 2 - Поля максимальных главных напряжений для начала движения стрясной доски назад-вверх

  
  

Запас усталостной прочности в зоне А:

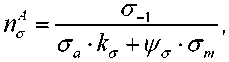
где <т__г - предел выносливости, для материала листов борта сталь 09Г2С для асимметричного цикла с., = 230 МПа;

Umax - максимальное напряжение цикла

Омах = 52,3 МПа (см. рисунок 2);

омм - минимальное напряжение цикла;

omin = -2,91 МПа (см. рисунок 3);

a_a - амплитуда напряжений цикла согласно [2];

= І5^ о^_) = (52.3 +2.91) =    мпд

2             2

где ко - эффективный коэффициент концентрации ат - среднее напряжение цикла согласно [2]. напряжений, для таврового сварного шва ко = 2,6 со гласно [1];

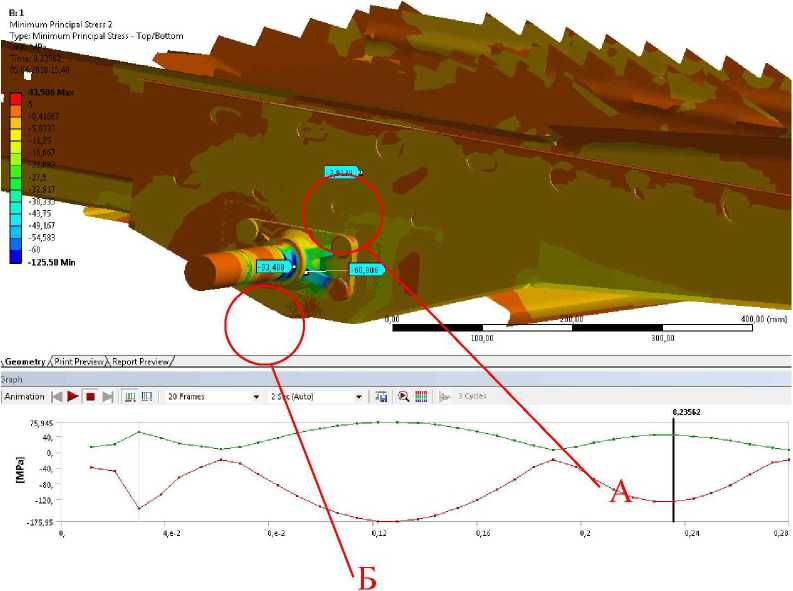
Рисунок 3 - Поля минимальных главных напряжений для начала движения стрясной доски вперед-вниз

l£j™±22™J ₌ (52.3 2,91) _{= 2 мПа}

2             2

где у_а - коэффициент чувствительности материала к асимметрии цикла, \у_о = 0,15.

Тогда минимальный запас усталостной прочности в зоне А:

° 27,6-2,6 + 0,15-24,7      '

запас усталостной прочности в зоне Б:

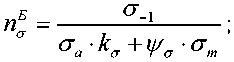
где а_л - предел выносливости, для материала оси сталь 40Х, 240-280 НВ для асимметричного цикла ст.] = 380 МПа;

Омах - максимальное напряжение цикла умах — 101,7 МПа (см. рисунок 2);

умах - минимальное напряжение цикла

Умш = -93,4 МПа (см. рисунок 3);

Оа - амплитуда напряжений цикла согласно [2];

17МАХ  ^МВГ

(101.7 + 93,4) 2

-97,5 МПа,

где кс - эффективный коэффициент концентрации напряжений ко = 1; так как технологические факторы от сутствуют, а геометрическая концентрация учтена в расчете;

у,„ - среднее напряжение цикла согласно [2];

101,7-93,4   , .----------— ~ 4,5 МПа, 2

(Ю)

где цг_а - коэффициент чувствительности материала к асимметрии цикла, у/_т = 0,15.

Тогда минимальный запас усталостной прочности в зоне Б:

380 ______

297,5-1 + 0,15-4,5

= 3,87.

Заключение. Важным условием повышения точности расчета запасов усталостной прочности конструкций является точное определение параметров циклов перемены напряжений в наиболее нагруженных зонах, для чего необходим анализ всех возможных режимов нагружения конструкции с выявлением наиболее опасных режимов.

Метод конечных элементов при достаточно высоком качестве конечно-элементной сетки позволяет определить локальное повышение действующих напряжений, связанное с особенностями геометрии конструкции. Поэтому при назначении расчетных коэффициентов концентрации напряжений необходимо учитывать только технологические факторы, оказывающие влияние на локальное повышение напряжений (сварные швы, шероховатость поверхности, переходы зон с различной твердостью, натяг и т.д.).

В результате расчета были определены циклы перемены главных напряжений и запасы усталостной прочности с учетом технологических факторов повышения локальных напряжений в наиболее нагруженных элементах стрясной доски зерноуборочного комбайна КЗС-1119Р.