Определение зависимости от температуры коэффициента парного взаимодействия компонентов систем пропан-нормальный гексан, пропан-нормальный гептан для уравнения состояния Пенга - Робинсона

Начиная с прошлого века и по наши дни научные деятели всех стран проводили интенсивные исследования, которые были нацелены на усовершенствование методов описания фазового равновесия систем природных углеводородов. В большей мере направленность изучения определяется потребностями практики: острой необходимостью роста качества проектирования и эксплуатации нефтяных и газоконденсатных месторождений, определения оптимальных технологических условий промысловой обработки, транспортировки и заводской переработки добываемого сырья.

Как показали исследования, более верным уравнением среди других является уравнение состояния Пенга-Робинсона. Наиболее результативное применение уравнений состояния для моделирования фазового равновесия природных углеводородов может быть существенно при наличии матрицы коэффициентов парного взаимодействия компонентов смесей. Параметр коэффициент парного взаимодействия (КПВ), характеризует степень взаимодействия между отдельными парами веществ. Эти коэффициенты приняты постоянными, вне зависимости от температуры. В реальности это вносит погрешность в расчеты. В связи с этим целью работы является расчет значений КПВ, в зависимости от температуры для уравнения состояния Пенга-Робинсона для 2 бинарных систем (пропан-нормальный гексан и пропан-нормальный гептан), выявление оптимальных значений КПВ для исходных температур для каждой пары веществ и сравнение стандартных значений КПВ с полученными данными.

Для определения оптимального коэффициента парного взаимодействия необходимы данные по реальному равновесному состоянию систем при различных температурах и давлениях. Данные были взяты из результатов экспериментов, проведенных в 60-70хх годах ХХ века.

Ниже на рисунке-1 представлена блок-схема использованной программы Fortran и C++ для поиска и проверки оптимального коэффициента парного взаимодействия.

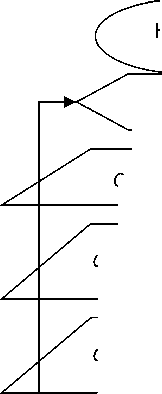
Считывание Pi

Считыван ие х Э

y h =	= i	— У Э
х Э =	= i	-x h

^С 12 = ^С 12п ; ^C 12fc ; ^С 12Д

Начало i=1, N

Считывание у Э

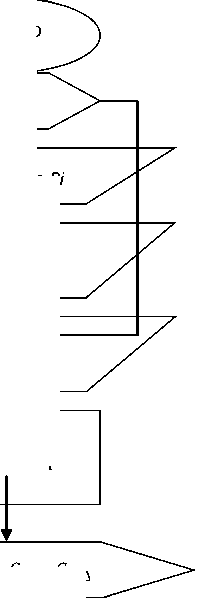
Fun1=0; Fun2=0

i=1, N

P=Pi

Расчет фазовых равновесий

Х Э - ХЦ

Fu^ = Fun1 +

X u

У Э

Fun₂ = Fun₂ +

-

У Э 1

^|

Fun1; Fun

n     1

Fun =-

1 N n     1

Fun 2 =-

2 N

Fun1

Fun2

Fun =0.5 ( Fun₁ + Fun₂ )

; Fun; Сц

Конец

Рисунок 1 – Блок–схема расчета

Расчет равновесного состава паровой и жидкой фазы проводится для бинарной системы пропан–н–гексан при всех температурах. Затем необходимо для каждой температуры определить такое значение КПВ, при котором значение Funk будет принимать минимальное значение.

Для этого задав в программе интервал КПВ (в нашем случае от –0,1 до 0,2; с шагом 0,02), внутри которого будет происходить расчет, выявим значение коэффициента с минимальным значением Funk . Получив результат, необходимо повторить расчет, задав интервал, вокруг полученного значения КПВ.

Таблица 1– Ошибки расчета системы пропан–н–гексан при T=410,78 К

КПВ	Относительна ошибка расчета в жидкой фазе, д.ед.	Относительная ошибка расчета в паровой фазе, д.ед.	Суммарная ошибка расчета системы, д.ед.
–0,1	0,2547	0,2163	0,2355
–0,08	0,2236	0,2121	0,2179
–0,06	0,1933	0,208	0,2006
–0,04	0,1637	0,2039	0,1838
–0,02	0,1343	0,1997	0,167
0	0,1111	0,1955	0,1533
0,02	0,0915	0,191	0,1413
0,04	0,0718	0,1862	0,129
0,06	0,0507	0,1806	0,1157
0,08	0,0329	0,1739	0,1034
0,1	0,0499	0,1655	0,1077
0,12	0,0841	0,1559	0,12
0,14	0,1179	0,1461	0,132
0,16	0,1485	0,1389	0,1437
0,18	0,177	0,1372	0,1571
0,2	0,2044	0,1349	0,1697

Для системы пропан–н–гексан, при T= 410,78 К , КПВ с приближенно минимальным Funk (суммарная ошибка расчета системы) равен C12=0,08 . Новый интервал, вокруг полученного значения КПВ необходимо просчитать с мелким шагом – 0,0001, для определения точного значения КПВ и Funk . В итоге получаем, что оптимальным коэффициентом парного взаимодействия является C12=0,0812, так как при использовании данного значении достигается минимальное значение Funk =0,1032.

Результаты подбора оптимального КПВ для системы пропан–н–гексан приведены в таблице и изображены на рисунках.

Относительная ошибка расчета                        о      Относительная ошибка расчета

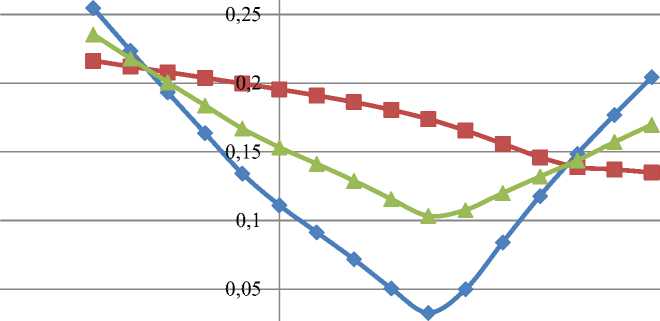
ошибка по жидкой фазе

-■- ошибка по паровой фазе

—*— суммарная ошибка

15       -0,1       -0,05        0        0,05       0,1        0,15       0,2       0,25

Рисунок 2 – Распределение относительных ошибок по КПВ при Т=410,78К

Рисунок 3 – Распределение относительных ошибок по КПВ при Т=377,44К

0,3

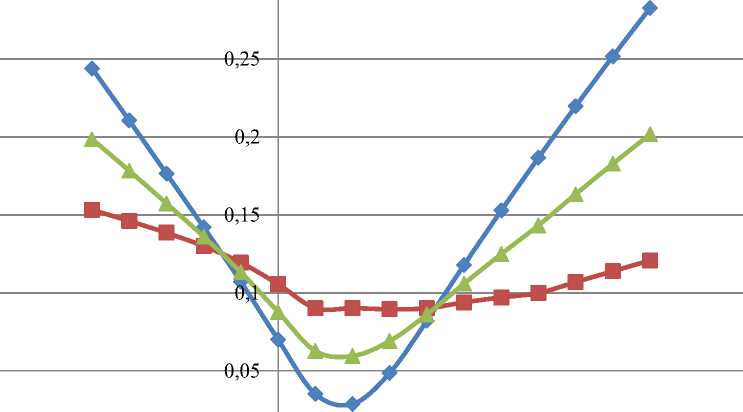
—♦— ошибка по жидкой фазе

—■- ошибка по паровой фазе

—*— суммарная ошибка

15      -0,1      -0,05       0        0,05       0,1       0,15       0,2       0,25

Таблица 2 – Оптимальное КПВ при заданных температурах

Т, оС	Коэффициент парного взаимодействия
71,11	0,0287
104,44	0,037
137,78	0,0812

Определение зависимости производится с помощью графиков и аппроксимации данных, полученных в ходе расчетов.

л CL

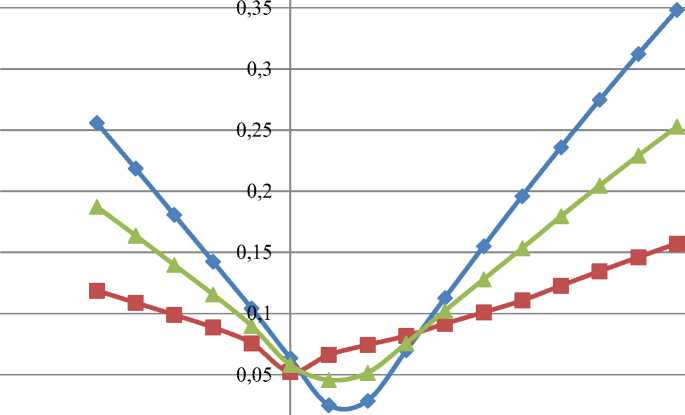
—Ф— ошибка по жидкой вазе

-■- ошибка по паровой фазе

—*— суммарная ошибка

-0,15       -0,1       -0,05        0         0,05        0,1        0,15        0,2        0,25

Рисунок 4 – Распределение относительных ошибок по КПВ при Т=344,1 К

Из графиков можно примерно определить приближенное значение КПВ с минимальным значением Funk . А более точное его значение вычисляется в программе и представлено в таблице.

КПВ

График зависимостей значений коэффициентов парного взаимодействия от температуры для системы пропан–н–гексан представлена ниже.

0,09

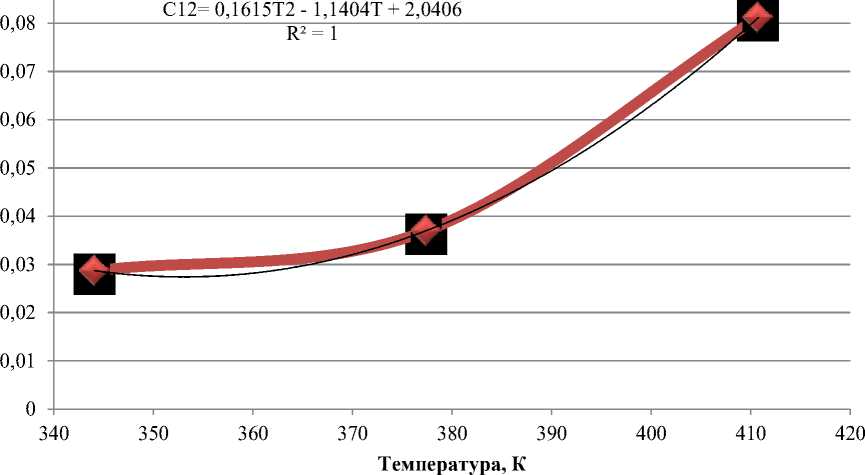
Рисунок 5 – Зависимость КПВ от температуры для системы пропан–н– гексан

Ниже представлена таблица с результатами для системы пропан–н– гексан.

Таблица 5 – Данные для системы пропан–н–гексан

T, К	Точное значение КПВ	Аппроксимированное значение КПВ
344,11	0,0287	0,0287
377,44	0,037	0,0370
410,78	0,0812	0,0812

Зависимость КПВ от температуры, для системы пропан–н–гексан запишется в виде уравнения (1):

C₁₂=0,1615-T 2 -1,1404-T+2,0406. (1)

Для аппроксимации использовался полином 2–й степени, так как он достаточно описывает изменение коэффициента парного взаимодействия от температуры. Из рисунка 4 видно, что качество аппроксимации для системы пропан–н–гексан высоко, так как показатель аппроксимации для системы R2 близок к 1 (в данном случае, он равен 1). На графиках можно заметить только один минимум. Для улучшения показателя аппроксимации можно увеличивать степень полинома, в этом случае произойдет ухудшение вида графика аппроксимации. Также можно применять аппроксимацию по нескольким, предварительно разбитым, участкам температур. Но в этом случае уточнение КПВ усложняется.

Для полученных значений КПВ необходимо вычислить относительные ошибки расчета – Funk. Чтобы затем сравнить с аналогичными показателями, для стандартных значений C12.

Таблица 4 – Сравнение средней ошибки расчета при стандартном и переменном КПВ по паре веществ пропан–н–гексан

	Ошибки при переменном КПВ			Ошибки при КПВ=0,03
T, К	Жидкая фаза	Паровая фаза	Общая	Жидкая фаза	Паровая фаза	Общая
344,11	0,0354	0,087	0,0612	0,0382	0,0874	0,0628
377,44	0,0462	0,097	0,0716	0,0377	0,0974	0,0676
410,78	0,321	0,1767	0,2489	0,4101	0,1984	0,3042

Из представленной таблицы видно, что практически по всем точкам температуры удалось добиться снижения средней ошибки расчета. Однако есть точка, в которой средняя ошибка увеличилась: 377,44 К. Это обусловлено тем, что для расчета использовался коэффициент парного взаимодействия, полученный по аппроксимации. Если использовать точное значение оптимального коэффициента парного взаимодействия, то ошибка уменьшается до 0,06.

В таблице 5 показано снижение средней ошибки расчета по двум системам веществ.

Таблица 5 – Сравнение средней ошибке по парам веществ

Пара веществ	Средняя ошибка при постоянном КПВ, %	Средняя ошибка при переменном КПВ, 5	Уменьшение средней ошибки, %
Пропан–н–гексан	14,5	12,7	1,8
Пропан–н–гептан	8,6	8,4	0,2

Как видно из таблицы, средняя ошибка по расчетам с переменным КПВ упала на 1 процент. В основном уменьшение ошибки расчета для данных бинарных систем в значительной степени, происходит за счет уменьшения ошибки по жидкой фазе, изменения ошибки расчета по паровой происходит незначительно. Таким образом, применение коэффициента парного взаимодействия, зависящего от температуры, для данных систем, позволяет незначительно уточнить получаемые результаты по составам фаз при использовании в расчетах уравнения Пенга – Робинсона.