Определение зависимости влияния параметров гранулометрического состава измельченного материала на энергетические параметры дезинтеграции
Автор: Клыков Юрий Георгиевич, Гуриев Тамерлан Созырикоевич
Журнал: Горные науки и технологии @gornye-nauki-tekhnologii
Статья в выпуске: 10, 2012 года.
Бесплатный доступ
Рассмотрены зависимости влияния крупности измельченного материала и его удельной поверхности на величину энергопотребления процесса измельчения.
Измельчение, гранулометрический состав, деформация, энергопотребление
Короткий адрес: https://sciup.org/140215412
IDR: 140215412
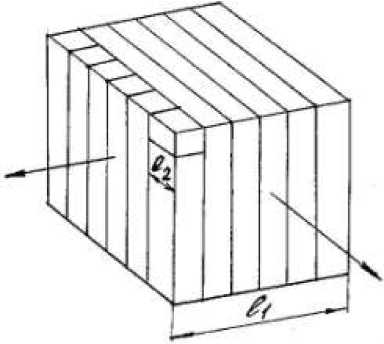
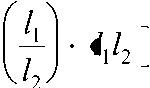
Список литературы Определение зависимости влияния параметров гранулометрического состава измельченного материала на энергетические параметры дезинтеграции
- Хуэто А.А., Тихонов О.Н. Прогноз энергии измельчения с учетом гранулометрических характеристик материалов.//Изв. Вузов. Цветная металлургия, 1992. -№3-4.
Статья научная
