Определение зоны допустимых перемещений ротора электродвигателя-маховика с активным магнитным подвесом
Автор: Поляков М.В.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Авиационная и ракетно-космическая техника
Статья в выпуске: 4 т.17, 2016 года.
Бесплатный доступ
Приведены основные преимущества активных магнитных подшипников при использовании их в качестве опор роторов электродвигателей-маховиков систем ориентации и стабилизации космических аппаратов. Обоснована необходимость в устройстве арретирования, обеспечивающем жесткую механическую фиксацию ротора относительно корпуса электродвигателя-маховика не только при его транспортировке и выводе космического аппарата на орбиту, но и при возникновении нештатных ситуаций в процессе орбитальной эксплуатации. Предложено устройство арретирования, содержащее страховочные подшипники, установленные на конических фиксаторах, перемещающихся в осевом направлении под действием сил притяжения электромагнитов и постоянных магнитов. Разработана методика определения требуемого перемещения фиксаторов, при котором одновременно обеспечивается бесконтактная левитация ротора в магнитном поле в штатном режиме работы и исключается возможность контакта ротора со статорными элементами системы активного магнитного подвеса в аварийных ситуациях. Рассматриваются различные варианты смещения ротора относительно его номинального положения: поступательные перемещения, повороты вокруг поперечной оси электродвигателя-маховика, а также случаи одновременного поступательного и углового перемещения. Исходя из характера динамического поведения вращающегося ротора в активном магнитном подвесе, рассчитываются результирующие колебания ротора, представляющие собой сумму колебаний его центра масс вдоль поперечных осей, обусловленных остаточной статической неуравновешенностью, и угловых колебаний вокруг данных осей под действием моментной неуравновешенности. В ходе анализа вынужденных колебаний и частотного анализа ротора рассчитываются собственные частоты, соответствующие им моды колебаний и амплитудные значения перемещений элементов ротора с учетом коэффициента жесткости системы активного магнитного подвеса. Разработанная методика позволяет не только судить о достаточности осевого перемещения фиксаторов устройства арретирования, исключающего возможность контакта ротора и статорных элементов системы активного магнитного подвеса, но и проверить отсутствие контакта вращающегося ротора с другими элементами электродвигателя-маховика, например, статорами электродвигателя и датчиком положения ротора.
Электродвигатель-маховик, устройство арретирования, страховочные опоры, активный магнитный подвес
Короткий адрес: https://sciup.org/148177630
IDR: 148177630 | УДК: 621.822.6
Текст научной статьи Определение зоны допустимых перемещений ротора электродвигателя-маховика с активным магнитным подвесом
Введение. В настоящее время активные магнитные подшипники (АМП) находят все большее применение в различных областях промышленности. АМП широко используются в газоперекачивающих агрегатах, в токарных, фрезеровальных, шлифовальных станках, в различных высокоскоростных роторных машинах [1–4]. Перспективно использование АМП и в космической технике, в частности, в качестве опор роторов электродвигателей-маховиков (ЭДМ) систем ориентации и стабилизации космических аппаратов [3; 5].
Основные преимущества АМП заключаются в отсутствии механического контакта между вращающимися и неподвижными элементами ЭДМ в штатном режиме работы, а также в возможности управления жесткостью и демпфированием системы АМП непосредственно в процессе работы ЭДМ. Бесконтактная левитация ротора в магнитном поле исключает механический износ элементов ЭДМ, снижает моменты трогания и сопротивления вращению, исключает необходимость в смазке, а также обеспечивает увеличение срока службы и возможность повышения рабочего диапазона частоты вращения ротора. Варьирование упруго-демпферными характеристиками магнитного подвеса позволяет значительно снизить вибрацию и связанные с ней помеховые силы и моменты сил, обусловленные остаточной динамической неуравновешенностью ротора ЭДМ.
Однако, несмотря на достаточно высокую надежность систем АМП, при разработке ЭДМ с магнитными подшипниками необходимо принимать во внимание возможность их отказа. Исходя из этого, любые роторные машины с магнитными опорами содержат узел страховочных подшипников (СП). В соответствии с ГОСТ Р ИСО 14839-1–2011 [6] СП представляет собой вспомогательный подшипник в системе АМП, предназначенный для ограничения перемещений ротора и предотвращения его контакта с поверхностью статора АМП. Помимо предотвращения контакта ротора со статорными элементами ЭДМ в нештатных режимах, СП обеспечивают выбег вращающегося ротора либо до его полной остановки, либо до возобновления работы системы АМП. В качестве СП преимущественно используются подшипники качения либо скольжения [3; 7].
Одним из основных параметров СП является зазор – половина разности между внутренним диаметром радиального СП и внешним диаметром цапфы ротора в этом подшипнике (радиальный зазор) или расстояние между торцевой поверхностью упорного СП и заплечиком вала (осевой зазор) [6]. Обычно зазоры в СП составляют примерно половину зазоров в АМП [8; 9]:
δр.СП = 0,5δр.АМП;
δо.СП = 0,5δо.АМП, где δр.СП – зазор в радиальном СП (допустимое перемещение ротора в радиальном направлении, рис. 1); δр.АМП – зазор в радиальном АМП; δо.СП – зазор в осевом СП (допустимое перемещение ротора в осевом направлении); δо.АМП – зазор в осевом АМП.
Однако при использовании системы АМП в ЭДМ введения узла СП по ряду причин недостаточно для обеспечения надежной работы и требуемого срока службы прибора.
Во-первых, воздействие внешних механических нагрузок при транспортировке ЭДМ, выводе космического аппарата на орбиту вызывает интенсивные колебания ротора в СП, результатом которых являются ударные нагрузки, действующие на СП и приводящие к их разрушению.
Во-вторых, в процессе орбитальной эксплуатации космического аппарата возникают нештатные ситуации, обусловленные внезапным отключением напряжения питания либо потерей устойчивости системы АМП. В таком случае ротор ЭДМ ляжет на СП, в которых будет осуществлять дальнейший выбег. Режим выбега ротора в СП зависит от силы трения между СП и вращающимся ротором [9], а также от отношения k динамических P и статических Q сил, действующих на ротор [10]:
k = P/Q.
Наиболее благоприятным является режим маятниковых колебаний, который соответствует k < 1, т. е. случаю, когда статические силы, действующие на ротор, превышают динамические.
Вместе с тем при выбеге ротора в СП в процессе орбитального функционирования космического аппарата статические силы Q , действующие на ротор, практически отсутствуют (вследствие невесомости), следовательно, k > 1. При этом происходит полный обкат ротором внутренней поверхности СП в направлении, противоположном вращению. Данный режим крайне нежелателен, поскольку вызывает значительную нагрузку на элементы СП, повышенную вибрацию ротора, что в итоге приводит к интенсивному износу и повреждению ротора и СП [9; 10].
Кроме того, зазоры в СП снижают жесткость опорного узла, уменьшая значения собственных частот системы «ротор–СП», что усиливает вибрационные явления, особенно если в процессе выбега ротор проходит через критические частоты. Также вследствие отсутствия надежных методик расчета и оценки работоспособности СП при аварийных выбегах существуют значительные сложности при проектировании СП и моделировании их работы [3; 10–14].
Указанные факторы приводят к тому, что СП могут выдержать аварийный выбег ротора крайне ограниченное количество раз.
Суммируя вышесказанное, необходимо отметить, что при использовании системы АМП в ЭДМ, помимо СП требуется устройство арретирования многократного действия, осуществляющее автоматическую механическую фиксацию ротора относительно корпуса ЭДМ как при его наземной транспортировке и выводе космического аппарата на орбиту, так и при орбитальном функционировании.
Устройство арретирования. Для фиксации ротора относительно корпуса ЭДМ предложено устройство арретирования [15; 16], совмещенное с узлом СП, которые установлены на двух валах-фиксаторах, расположенных с обоих концов вала ротора. Валы-фиксаторы могут реверсивно перемещаться в осевом направлении на расстояние ±δф (рис. 2), обеспечивая либо жесткую механическую фиксацию ротора относительно корпуса ЭДМ, либо его бесконтактную левитацию в магнитном поле системы АМП.
Преимуществом такого устройства является многократная автоматическая фиксация и центрирование ротора при возникновении нештатных режимов. В арретированном состоянии ротор вращается в СП аналогично традиционным ЭДМ с шарикоподшипниковыми опорами. Вибрации и нагрузки, действующие на СП в таком режиме, значительно меньше нагрузок, действующих в процессе выбега ротора в СП с зазором .
Определение зоны допустимых перемещений ротора ЭДМ в АМП. С целью обеспечения безопасного режима работы ЭДМ с АМП необходимо определить требуемое осевое перемещение вала-фиксатора ±δ ф . С одной стороны, данное перемещение должно быть достаточным для того, чтобы ротор ЭДМ мог совершать колебания относительно своего номинального положения, вызванные остаточной динамической неуравновешенностью и различными внешними воздействиями. С другой стороны, должна быть полностью исключена возможность механического контакта и повреждения ротора и статорных элементов системы АМП и ЭДМ в целом.
Перемещение вала-фиксатора ±δ ф определяется зоной возможных смещений ротора ЭДМ в активных устройствах системы АМП (радиальными δр.АМП и осевыми δо.АМП зазорами), расстояниями между данными устройствами и геометрической формой контактных поверхностей ротора и вала-фиксатора.
Простейшим случаем смещения ротора от его номинального положения является линейное перемещение в осевом δ Z и радиальном δ X направлении, как показано на рис. 3.
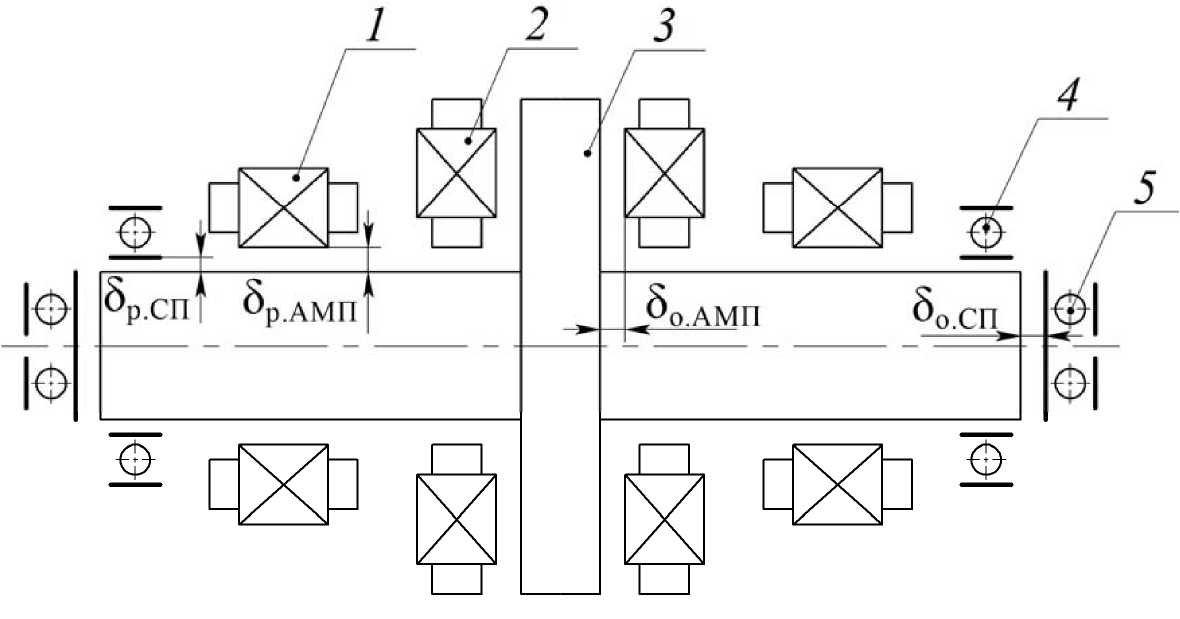
Рис. 1. Зазоры в СП и АМП:
1 – радиальный АМП; 2 – осевой АМП;
3 – ротор; 4 – радиальный СП; 5 – осевой СП
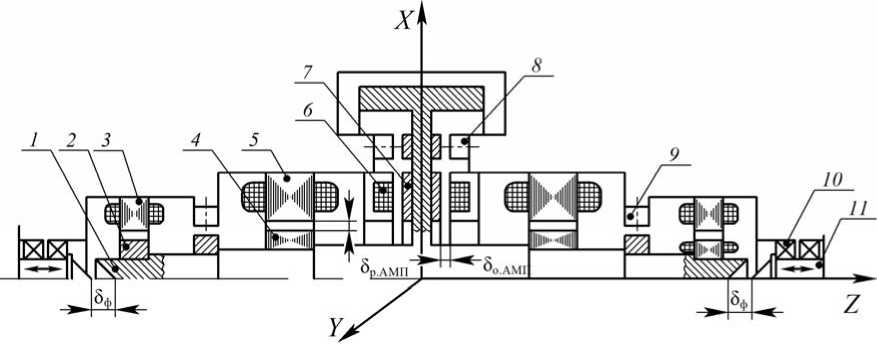
Рис. 2. Схема ЭДМ с системой АМП:
1 – ротор; 2 , 3 – ротор и статор датчика положения ротора; 4 , 5 – ротор и статор радиальной электромагнитной опоры; 6 , 7 – статор и ротор осевой электромагнитной опоры; 8 , 9 – датчики осевого и радиального зазора АМП; 10 – СП; 11 – вал-фиксатор
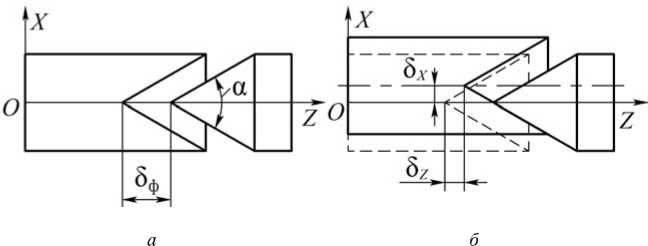
Рис. 3. Схема линейных перемещений ротора: разарретированное номинальное положение ( а ); радиальное δ X и осевое δ Z смещение ротора ( б )
В общем случае при одновременном перемещении по координатам Х и Z зазоры δ р.СП , δ о.СП в зависимости от перемещения δ ф и угла конуса контактной поверхности α определяются по выражению
Z
= 8 Ф
^^^^^^в
8 X
tg
а
Из данного выражения можно получить частные случаи перемещения по одной из координат. Максимальное перемещение по координате Z (осевой зазор в СП δ о.СП ) при δ Х = 0
δ Z = δ о.СП = δ ф .
Максимальное перемещение по координате Х (радиальный зазор в СП δ р.СП ) при δ Z = 0
Га)
8 x = 8 р.сп = 8 ф tg I 2 I .
Осевые и радиальные зазоры в СП равны между собой только при α = 90°, в остальных случаях допустимое перемещение по одной из координат больше, чем по другой. Поскольку перемещение фиксатора δ ф является максимальным осевым зазором δ о.СП , то целесообразно задавать его значение, выполняя условие δ ф < δ о.АМП , и рассчитывать соответствующее допусти-
мое радиальное перемещение δ р.СП для заданного угла α. Например, зазоры δ о.АМП и δр.АМП в системе АМП составляют 0,4 мм, диапазон перемещения фиксатора δ ф = 0,3 мм. Значения допустимого радиального перемещения δ р.СП при различных углах α приведены на рис. 4, из которого можно сделать вывод, что углы α > 106º являются недопустимыми, поскольку радиальное перемещение в СП δ р.СП превышает радиальный зазор в АМП δ р.АМП.
Следующим вариантом смещения ротора относительно своего номинального положения в системе АМП является его угловой поворот вокруг поперечной оси Y . В данном случае необходимо определить максимальный угол β, на который может повернуться ротор, а также соответствующее данному углу линейное смещение наружной поверхности ротора в радиальном направлении δ X β .
Радиус окружности, по которой перемещается точка А, расположенная на контактной поверхности ротора на наибольшем удалении от его геометрического центра, определяется выражением d2
4,
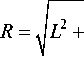
где L – расстояние от геометрического центра ротора до торца его вала (рис. 5); d – диаметр вала ротора.
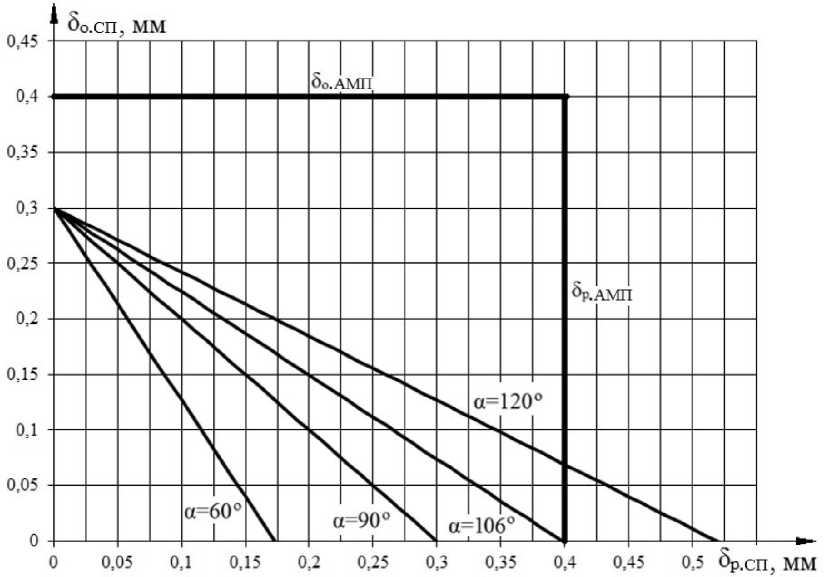
Рис. 4. Зависимость допустимого радиального перемещения δр.СП от осевого перемещения δо.СП при различных углах конуса контактной поверхности α
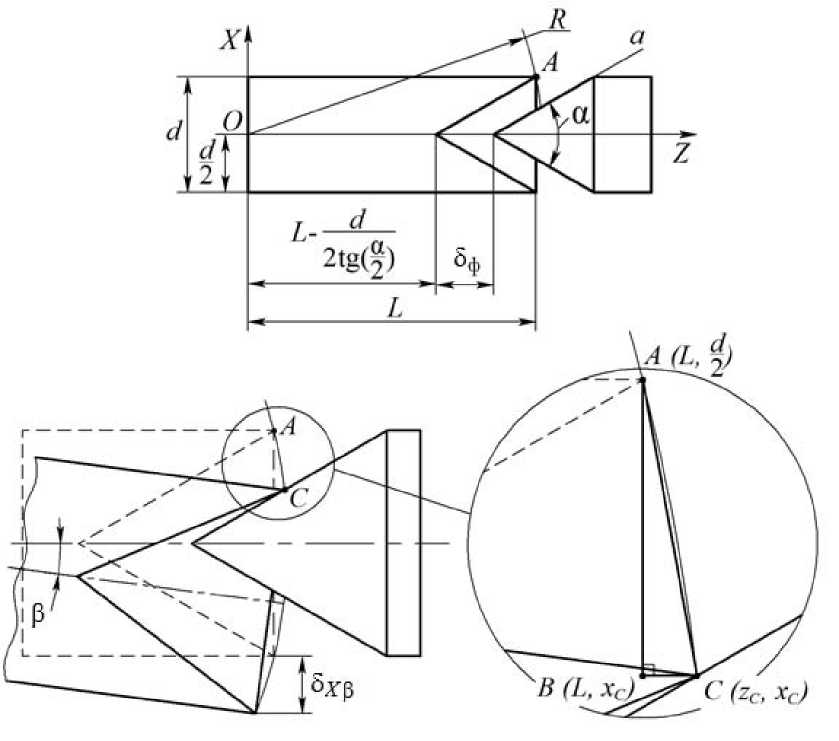
Рис. 5. Угловой поворот ротора вокруг поперечной оси
Уравнение прямой a , характеризующее контактную поверхность фиксатора, можно записать следующим образом:
л
x =
z -
L
d fa
2tg I 2
+ 0 Ф
f a I tg IT J .
Координаты точки пересечения С контактной поверхности фиксатора и окружности, по которой перемещается точка А , определяются из решения уравнения
d 2
,2 + —
z 2 +
z
L
d fa
2tg I 2
+ 0 Ф
f a tg 1 2
.
Данное уравнение приводится к квадратному, его решением является координата z С , соответствующая точке пересечения окружности, по которой перемещается точка А при повороте ротора, с прямой a , характеризующей контактную поверхность фиксатора. Координата xC точки пересечения рассчитывается по уравнению (1) подстановкой z C вместо z .
Максимальный угол поворота можно определить по дуге окружности, ограниченной начальным положением точки А и точкой пересечения C . Вследствие малости перемещений дугу АС можно считать прямой, ее длина определяется из треугольника АВС :
AC = 1 (
.
Максимальный угол поворота (в градусах)
P = 360----.
2 n R
Радиальное смещение наружной поверхности вала ротора, обусловленное его поворотом на угол β,
d
0 х p 2 x C .
Рассмотренные варианты линейных перемещений и угловых поворотов являются частными случаями отклонения ротора от номинального положения. Естественно, в процессе работы ротор может совершать одновременно как линейные, так и угловые смещения. Однако в таком случае максимальное отклонение ротора от номинального положения не превышает значений δ р.СП , δ о.СП , β, рассчитанных ранее для частных вариантов, что возможно получить, учитывая соответствующие радиальные и осевые смещения ротора в уравнениях для расчета углового поворота вокруг поперечной оси.
Таким образом, результатом геометрического решения задачи определения зоны допустимых перемещений ротора являются максимальные линейные смещения в радиальном и осевом направлениях δ р.СП , δ о.СП , а также значение максимального угла β его поворота вокруг поперечной оси.
Динамическое поведение вращающегося ротора в магнитном подвесе. В процессе вращения главная
центральная ось инерции ротора неизбежно совершает линейные и угловые колебания, основной причиной которых является его остаточная динамическая неуравновешенность, являющаяся суммой остаточных статической и моментной неуравновешенностей. Статическая неуравновешенность приводит к линейным колебаниям центра масс ротора в радиальном направлении, моментная – вызывает угловые колебания главной центральной оси инерции ротора. Для обеспечения нормальной работы ЭДМ амплитуды данных колебаний не должны превышать максимально допустимых перемещений в страховочных опорах δ р.СП , δ о.СП , β, рассчитанных при геометрическом решении задачи определения зоны допустимых перемещений ротора.
Линейные и угловые колебания симметричного ротора как жесткого тела по осям X и Y (см. рис. 2) описываются следующими уравнениями [3]:
mx + 2 Bx + 2 Cx = me to cos ( to t ) ;
my + 2 By + 2 Cy = me to sin ( to t ) ;
J э Ф X + J o tot p Y + R Ф X + D ф X = ( J э - J о ) Yto 2 cos ( to t ) ;
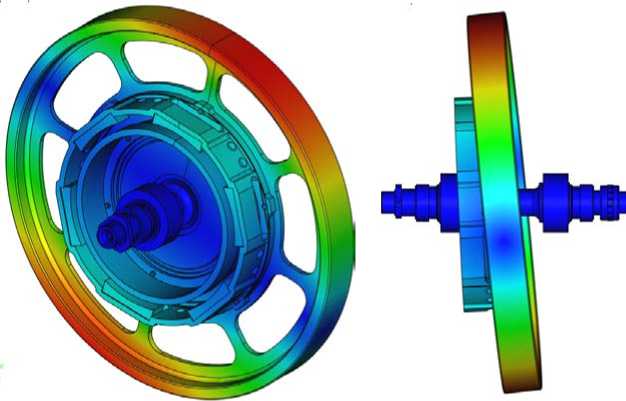
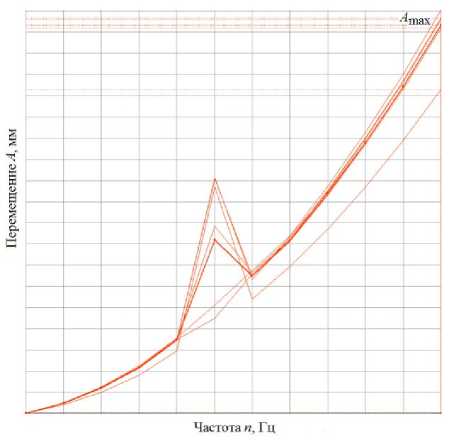
_ JэфY - Joto Решением системы уравнений (2) являются амплитуды вынужденных линейных и угловых колебаний ротора по осям X и Y. Амплитуда вынужденных колебаний геометрического центра ротора по любому из радиальных направлений, возникающих вследствие его статической неуравновешенности [3], meto2 . (2 C - mto2)2 + 4 B2to2 Амплитуда вынужденных угловых колебаний геометрической оси ротора [3] Ф с = ( Jэ -Jо )Yto2 .2)2 + R2to2 . Амплитуда результирующих колебаний точки ротора, максимально удаленной от его геометрического центра, AS = AC + L sin Ф C. Расчетные максимальные амплитуды колебаний ASmax и Фmax (рис. 6) не должны превышать максимально допустимых перемещений δр.СП и β, рассчитанных при решении геометрической задачи. В противном случае необходимо либо увеличить зазоры в СП (увеличить перемещение фиксатора δф), либо изменить параметры системы магнитного подвеса. Рис. 6. Графики зависимости амплитуды радиальных (а), угловых (б) и результирующих (в) колебаний ротора от его угловой скорости ω Недостатком такого расчета является рассмотрение ротора как абсолютно жесткого тела, при этом не учитываются его собственные частоты и изгибные формы колебаний, а также деформации его элементов под действием центробежных сил, возникающих в процессе его вращения. Анализ вынужденных колебаний ротора и определение перемещений его элементов с учетом изгибных мод колебаний целесообразно проводить с помощью систем конечно-элементного анализа. Перед этим необходим частотный (модальный) анализ исследуемого ротора с целью выявления значений его собственных частот и соответствующих им изгибных форм колебаний, а также определения областей ротора, в которых наблюдаются максимальные смещения элементов от номинального положения [17]. Например, по результатам частотного анализа ротора ЭДМ с АМП (рис. 7) установлено, что на первой собственной частоте максимальное отклонение от номинального положения наблюдается в его ободе (рис. 8). При проведении анализа вынужденных колебаний ротора целесообразно разместить на ободе в точках максимальных смещений виртуальные датчики, регистрирующие результирующее перемещение данной точки и перемещения по отдельным координатам. Кроме того, датчики можно установить в других точках, например в области контактной поверхности вала ротора, для получения актуальной информации о смещениях ротора в выбранных областях. Применение виртуальных датчиков позволяет по результатам анализа вынужденных колебаний автоматически формировать амплитудно-частотную характеристику, соответствующую выбранной точке ротора (рис. 9). Максимальные перемещения Amax точек ротора, определенные при анализе вынужденных колебаний, не должны приводить к его касанию со статорными элементами ЭДМ. В противном случае необходимо либо скорректировать конструкцию ЭДМ (увеличить зазоры между ротором и статорами ЭДМ, изменить форму ротора с целью повышения его жесткости, увеличения собственных частот и уменьшения амплитуды его изгибных колебаний), либо изменить параметры системы магнитного подвеса. Заключение. Таким образом, разработанная методика определения зоны допустимых перемещений ротора, устанавливающая зависимости между перемещением вала-фиксатора ±δф, зазорами в страховочных подшипниках δр.СП, δо.СП., зазорами в активных устройствах системы магнитного подвеса δр.АМП, δо.АМП, учитывает характер динамического поведения вращающегося ротора в системе АМП. Использование данной методики позволяет определить оптимальное значение перемещения фиксаторов δф, обеспечивающее бесконтактное вращение ротора в магнитном поле, создаваемом системой АМП в штатном режиме работы, и исключить возможность контакта ротора со статорными элементами системы АМП и другими элементами ЭДМ в аварийных ситуациях. а б Рис. 7. 3D-модель (а) и конечно-элементная модель (б) ротора ЭДМ Рис. 8. Форма колебаний ротора ЭДМ, соответствующая его первой собственной частоте Рис. 9. Зависимость перемещения в точках на ободе ротора от частоты вращения ротора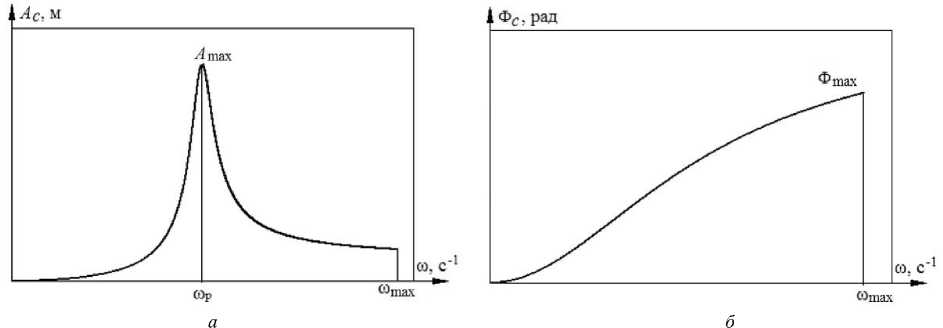

Список литературы Определение зоны допустимых перемещений ротора электродвигателя-маховика с активным магнитным подвесом
- Сарычев А. П. Разработка электромагнитных подшипников для серии компрессоров газоперекачивающих агрегатов//Вопросы электромеханики. 2009. Т. 110. С. 3-10.
- Поляхов Н. Д., Стоцкая А. Д. Обзор способов практического применения активных магнитных подшипников//Научное приборостроение. 2012. Т. 22, № 4. С. 5-18.
- Журавлев Ю. Н. Активные магнитные подшипники: теория, расчет, применение. СПб.: Политехника, 2003. 206 с.
- Schweitzer G., Maslen E. Active magnetic bearings. Theory, design and application to rotating machinery. Berlin: Springer, 2009. 535 p.
- Макриденко Л. А., Сарычев А. П., Верещагин В. П. Состояние и перспективы развития электромагнитных подшипников в ФГУП «НПП ВНИИЭМ»//Вопросы электромеханики. 2011. Т. 120. С. 3-12.
- ГОСТ Р ИСО 14839-1-2011. Вибрация. Вибрация машин вращательного действия с активными магнитными подшипниками. Ч. 1. Термины и определения. М., 2012. 16 с.
- Боровков М. Н., Белов С. Е., Новинский Э. Г. Разработка страховочных подшипников вертикальной турбомашины установки ГТ-МГР//Тр. Нижегородского государственного технического университета им. Р. Е. Алексеева. 2010. № 2 (81). C. 134-142.
- Верещагин В. П., Рогоза А. В., Савинова Т. Н. Методика проектирования электромагнитных подшипников//Вопросы электромеханики. 2009. Т. 113. С. 3-12.
- Леонтьев М. К. Давыдов А. Л., Дегтярев С. А. Динамика роторных систем, опирающихся на магнитные подшипники//Газотурбинные технологии. 2011. № 3. С. 16-22.
- Воловик А. П., Воронкин В. А. О выбеге роторов на страховочных подшипниках//Вопросы электромеханики. 2009. Т. 108. С. 12-16.
- Воловик А. П. Оценка работоспособности страховочных подшипников качения роторных машин на магнитном подвесе//Вопросы электромеханики. 2009. Т. 109. С. 7-14.
- Кайдалов В. Б., Патрушев В. Л., Руин А. А. Проблемы моделирования динамики ротора при отказе электромагнитных подшипников//Тр. Нижегородского государственного технического университета им. Р. Е. Алексеева. 2011. № 3 (90). C. 135-140.
- Белов С. Е., Кодочигов Н. Г., Патрушев В. Л. Аналитические исследования динамики вращения ротора при отказе резервных подшипников//Вестник Нижегородского университета им. Н. И. Лобачевского. 2011. № 4 (2). C. 63, 64.
- Кочетов Д. А., Кравцова Е. В. Исследование динамики ротора на магнитных и страховочных подшипниках в аварийных режимах//Тр. ВНИИЭМ. 1989. Т. 89. С. 50-61.
- Поляков М. В., Гладышев Г. Н., Лянзбург В. П. Устройство арретирования и страховочные опоры ротора двигателя-маховика в магнитном подвесе//Электронные и электромеханические системы и устройства: сб. науч. тр. Томск: Изд-во Том. политехн. ун-та, 2016. С. 329-336.
- Пат. 2574497 Российская Федерация, МПК G 01 C 19/26, B 64 G 1/28. Устройство арретирования ротора электродвигателя-маховика в магнитном подвесе/Поляков М. В., Гладышев Ю. Г., Гладышев Г. Н. и др. № 2014142834/11; заявл. 23.10.2014; опубл. 10.02.2016, Бюл. № 4.
- Снитко А. А., Корнилков Н. А., Леонтьев М. К. Роторная динамика компрессора с электромотором на АМП//Газотурбинные технологии. 2012. № 5. С. 28-34.


