Определяющее уравнение вязкоупругого поведения одноосно-ориентированных полимерных материалов и его применение к расчету диаграмм растяжения

Полимерные материалы и изделия на их основе нашли широкое применение практически во всех отраслях промышленности. Полимерные волокна, нити, пленки, композиционные материалы стали незаменимыми в качестве материалов бытового назначения, деталей автомобилей и т.д. В настоящее время трудно найти отрасль, которая не использовала бы пленочные материалы в виде покрытий, свободных пленок или изделий из них. При этом полимерные материалы, применяемые для различных целей бытового назначения, должны обладать соответствующими деформационными и прочностными свойствами. Данная работа посвящена моделированию и прогнозированию упругих и релаксационных свойств одноосноориентированных полимерных нитей и пленок. В качестве примера предлагаемый метод применен для прогнозирования точек диаграмм растяжения поликапроамидных (ПКА) пленочных нитей, являющихся перспективным материалом для использования его в бытовой технике.

Большинство ориентированных аморфно-кристаллических полимеров при наличии механических воздействий проявляют нелинейные реологические свойства. Для описания механизмов их поведения разработан ряд теорий нелинейной вязкоупругости [1-5], основанных на известном принципе наследственности Л. Больцмана. Современные теории нелинейной вязкоупругости отличаются видом ядра релаксации и обосновываются либо анализом большого числа экспериментальных данных, либо н екоторыми общими физическими аналогиями [6-11]. Использование гладких ядер в интегральном определяющем уравнении имеет ряд чисто математических удобств, что позво- ляет вполне удовлетворительно описывать широкий класс полимерных материалов.

Тем не менее, анализ поведения синтетических полимерных материалов в различных режимах деформирования показал, что уравнение напряженно-деформированного состояния можно представить в виде:

Ф ( б , 8 , а , 8 ) = 0 ,                  (1)

где: 6 - механическое напряжение; 8 - деформация; 6 - скорость изменения механического напряжения; 8 - скорость деформации.

Весьма сложная и многообразная надмолекулярная структура ориентированных аморфно-кристаллических полимеров [2, 3] определяет вязкоупругие свойства полимерных материалов. При деформировании материалов данного класса основную долю деформации составляет обратимая вязкоупругая часть деформации. В общем случае полную деформацию 8 можно представить в виде суммы упругой ( 8 y ), вязкоупругой, или конформационной ( 8 к ), и необратимой ( 8 н ) частей деформации.

Скачкообразность и длительность процессов деформирования свидетельствует о том, что все основные перестройки при деформировании полимеров происходят на мезоуровне с достаточно большими временами релаксации (10^-2 ^ 10¹) и определяются его надмолекулярной структурой. Таким образом, следует признать, что на мезоуровне полимеры в нагруженном состоянии могут находиться в различных квазиравновесных состояниях. Экспериментальным подтверждением данному выводу могут служить обнаруженные Б.М. Гинзбургом кристаллоподобные тяжи [12]. Наиболее правдоподобной является гипотеза о том, что на мезоуровне существует не менее двух устойчивых структур, которые в соответствии с терминологией, принятой в работе [13], будем называть активными конформационными элементами (АКЭ), природа которых для механического описания не имеет принципиального значения. Переход из одного состояния в другое сопровождается квантом деформации 5 . При таком подходе вязкоупругая часть деформации лимитируется обратимыми переходами АКЭ из одного состояния в другое.

В работе [13] выведено в явном виде определяющее уравнение вязкоупругого состояния (1) при условии, что высоты потенциаль

ных барьеров, разделяющих квазиравновесные состояния АКЭ, линейно зависят от уровня механического напряжения, что обычно принимается в большинстве теорий разрушения. В окончательном виде определяющее уравнение, полученное в работе [13], имеет вид:

d d т

8-

Е

6 7 1 Y 6 + е-— ch — U + —

V E о у

E о у

...

...

= q

Y 6

2 Ё 0 у

²           *

где: т = — exp[ - H ] - собственное безразмер н о

*U ное время; U =--- - приведенная энергия kБT

энергетического зазора между двумя квазирав-

новесными состояниями АКЭ; H

H k Б T

приведенная высота энергетического барьера между двумя квазиравновесными состояниями АКЭ; y * - приведенный структурно

чувствительный коэффициент; Е ₀ - модуль

упругости, определяющий упругую часть де формации; — - частота подхода к барьеру -Т0

константа для данного материала;

q =

5 m ₀

2 ch

Г U*)

V

у

- параметр, описывающий активирующую роль нагрузки; 5 - величина кванта абсолютной деформации при единичном конформационном переходе; m ₀ - число АКЭ на единицу длины.

Анализ решения определяющего уравнения (2) показывает, что данное уравнение в некоторых пределах вполне удовлетворительно описывает вязкоупругое поведение полимерных нитей.

Однако детальный анализ показывает, что в более широком диапазоне нагрузок имеются некоторые значимые отклонения от теории. Прежде всего, это вызвано тем, что высота энергетического барьера меняется за счет наличия упругой энергии АКЭ. Как известно, упругая энергия является квадратичной формой от

механического напряжения. Поэтому уравне- ется типичная S-образная диаграмма растяже

ние (2) в этом случае примет вид:

ния (кривая 2).

Т- ( s- x ) + ( е- x ) [ exp ( у x ²) + exp ( U * -у x ²) ] =

= qsh ( у x ² ) ,                               (3)

где: x = — - упругая часть деформации;

E 0

25 mn q =          ,. - Y - структурно-

[1 + exp( - U )]

чувствительный коэффициент, определяемый из эксперимента.

Рассмотрим применение уравнения (3) к изучению диаграмм растяжения, полученных с квазипостоянной скоростью растяжения s = const , а именно:

s ( 1 - x s ) + ( s- x ) e ^{Y x} + Ae ^{у x} = ...

... = qsh ( у x ² ) ,                            (4)

* здесь для краткости A = e .

Уравнение (4) представляет собой обыкновенное дифференциальное уравнение, задача Коши для которого s = 0 , x = 0 .

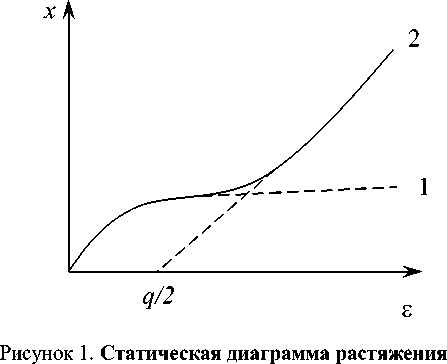
Рассмотрим сначала статическую диаграмму растяжения, для которой s ^ 0 . Име-

ем:

s = x +

q [1 - e ^{- 2 Y} x 2 ] 2[1 + A e ^{- 2 Y x 2} ]

Общий вид этой зависимости изображен на рис. 1. Физический смысл данной диаграммы достаточно очевиден. При малых деформациях основную роль играют упругие деформации, далее начинают «работать» конформационные переходы, т.е. происходит дополнительное ориентирование. Для гибкоцепных полимеров (кривая 1) разрушение может произойти раньше, чем все АКЭ перейдут в более устойчивое состояние. Для жесткоцепных (например, СВМ, Армос и т.д.) и среднежесткоцепных полимеров (полиэтилентерефталат) по мере увеличения уровня деформации происходит эффект насыщения, когда при наличии двух устойчивых состояний все АКЭ перейдут в ориентированное состояние. Далее работает только упругая часть деформации, т.е. получа-

В общем случае уравнение (4) не интегрируется в конечном виде.

В случае гибкоцепных полимеров ( у x ² <  1 ), уравнение (4) представляет собой уравнение Риккарти:

s x ‘ + q Y x ² + (1 + A ) x - (1 + A ) s - s = 0 . (6)

Путем стандартных замен переменных уравнение (6) превращается в уравнение Эйри:

У "( 0 ) -0 у = 0,                  (7)

решения которого выражаются через известные табулированные функции A i ( 0 ) и B i ( 0 ) Эйри

первого и второго рода, соответственно, здесь:

Г q у ( 1 + A ) ^ ^/з

0 = ----77----

4 ys- ( A + 1 ) 2

⁺      4 1 2

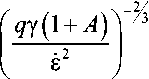
( A + ¹ ) _s

Z ( s ) = e ^{2 s} у ( s ) .

x =

s Z'

q y Z ’

Анализ результатов многочисленных

экспериментов для небольших скоростей де

формирования показал, что зависимость вида

диаграммы растяжения от s слабая. Для гиб

коцепных полимеров зависимость s ( x ) с точ-

2               _ ностью до s имеет вид:

q Y s ( x ) = x +         x

V ’       (1 + A)

2 q у s x

( 1 + A ) [ ( 1 + A ) + 2 q у x ]

2 q у ( 1 + A ) s ² [ ( 1 + A ) + 2 q у x ] ⁴

Считая £ малым параметром с точностью до £ в первой степени, решение уравнения (4) в общем виде для большинства высокоориентированных нитей и пленок можно представить так:

_q Г ¹ - e - 2 ^Y x ² 1

£( x) = x ++

• ^v ’       2 [ 1 + Ae ^—27 x ² 1

2 y q ^{( 1 +} A ) e -^{2 Y} x ² x

... + £-----------------;

1 + Ae 2 ^Y x ) + 2 y q ( 1 + A ) e 2 ^Y x x

Данное представление решения уравнения (4) предлагается использовать для прогнозирования диаграмм растяжения одноосноориентированных полимерных материалов.

В качестве объектов исследования рассматриваются одноосноориентированные пленочные нити на основе ПКА. Экспериментальные образцы ПКА различной степени вытяжки ( X =2.4; 4.1; 5.5) получены в лаборатории «Элементарных актов разрушения» в отделе Физики прочности Физико-технического института имени А.Ф.Иоффе РАН на установке путем многоступенчатой зонной ориентационной вытяжки прессованных пленок. Диаграммы растяжений, а также «семейства» релаксации напряжений и ползучести с восстановлением исследуемых объектов получены в лаборатории «Релаксационных явлений» кафедры Сопротивления материалов Санкт-Петербургского государственного университета технологии и дизайна.

Процессы ползучести с восстановлением и релаксации напряжения представляют собой наиболее простые варианты нагруженного состояния материала, поскольку один из параметров либо о при ползучести, либо е при релаксации напряжений поддерживается неизменным в течение эксперимента. Из диаграмм растяжений можно получить первоначальные сведения о прочностных и деформационных характеристиках исследуемых образцов, но сами по себе они не дают полного представления о физико-механических свойствах. Однако в них все-таки содержится важная информация о структурных изменениях. Для объективного оценивания физико-механических свойств ПКА необходимо изучение процессов ползучести и релаксации напряжений, анализ которых дает информацию о вязкоупругих свойствах материала.

Таким образом, для определения неизвестных констант, входящих в уравнение (4), использовались статические экспериментальные кривые ползучести и кривые релаксации напряжений [14, 15]. На рисунке 2 представлены экспериментальные зависимости деформации (кривые ползучести) и релаксирующего модуля от логарифмической шкалы времени (t i =60 с) для образцов предельной степени вытяжки ( X = 5.5).

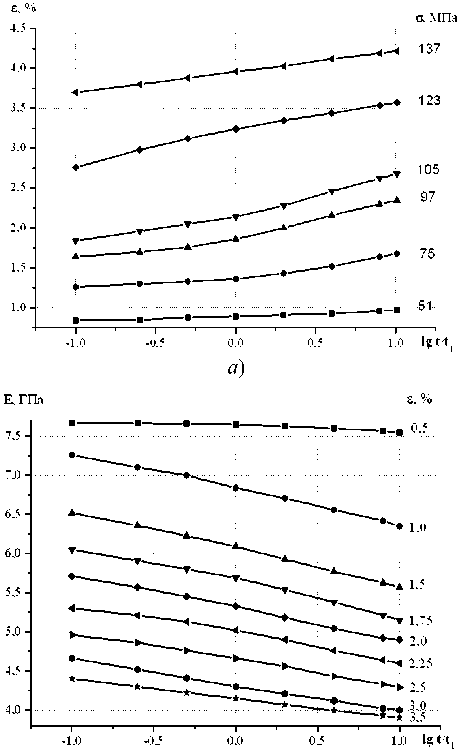
б

Рисунок 2. «Семейства» кривых ползучести ( а ) и релаксирующего модуля для образцов ПКА ( б)

Расчет более сложного режима деформирования, а именно, точек диаграмм растяжений производился по полученным значениям вязкоупругих характеристик и уравнению состояния (9).

Диаграммы растяжений исследуемых образцов (рис. 3) получены на универсальной установке Instron 1122 при скорости деформирования 100 мм/мин, базовой длине образцов 30 мм, температуре 21°С и относительной влажности 46%. Как можно видеть, вид диаграммы растяжения сильно зависит от степени вытяжки X образцов. Для предельно ориентированного образца диаграмма имеет обычный для капрона S-образный вид. Как и следовало ожидать, уменьшение λ до 4 приводит к значительному уменьшению разрывного напряжения σp, двукратному увеличению разрывной деформации εp, ʜo S-образный характер диаграммы при этом сохраняется. Существенно иной характер имеет диаграмма для образцов с λ=2,4. Как можно видеть, в данном случае продолжается существенная доориентация образца в процессе растяжения. Разрывная деформация

ε р достигает 100%, то есть образец удлиняется в

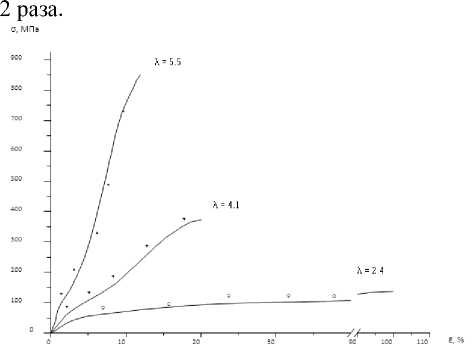
Рисунок 3. Экспериментальные диаграммы растяжения для образцов ПКА различной степени вытяжки

Как следует из графиков на рис. 3, расчетные значения вполне удовлетворительно согласуются с экспериментальными данными.

Таким образом, предложенное уравнение состояния (4) с квадратичной формой зависимости упругой энергии более точно позволяет описать и спрогнозировать поведение одноосноориентированных полимерных материалов.