Определяющие соотношения для материалов со свойствами, зависящими от вида деформированного состояния
Автор: Ломакин Е.В., Тишин П.В.
Статья в выпуске: 1, 2021 года.
Бесплатный доступ
Многие материалы демонстрируют зависимость механических свойств от вида напряженного или деформированного состояния. Наиболее заметно это проявляется в зависимости процессов сдвигового и объемного деформирования. К такого рода материалам относятся материалы, содержащие дефекты различного характера, например: горные породы, конструкционные графиты, бетон, некоторые марки стали, чугун, алюминий. Основные свойства этих материалов заключаются в отсутствии «единой кривой» связи между интенсивностью напряжений и интенсивностью деформаций. В условиях сдвига могут происходить объемные деформации. Указанные материалы могут описываться определяющими соотношениями, зависящими от параметра вида напряженного состояния, представляющего собой отношение первого инварианта тензора напряжений к интенсивности напряжений. Таким образом, эти определяющие соотношения дают зависимость компонент тензора деформаций от компонент тензора напряжений. Такие определяющие соотношения могут быть достаточно громоздкими и поэтому не допускают аналитического обращения для получения определяющих соотношений, дающих зависимость компонент тензора напряжений от компонент тензора деформаций. В работе предлагаются сравнительно простые определяющие соотношения, полученные в ходе анализа результатов испытаний различных материалов, свойства которых зависят от вида деформированного состояния. Выводятся условия на материальные константы, обеспечивающие единственность решения краевых задач. На основе экспериментальных данных по пропорциональному нагружению различных горных пород: известняка и талькохлорита, а также результатов механических испытаний нескольких марок бетона определяются постоянные математической модели. Проводится сопоставление результатов экспериментальных исследований с теоретическими зависимостями, предсказываемыми моделью. Устанавливаются ограничения на применимость предлагаемых определяющих соотношений.
Горные породы, бетон, известняк, талькохлорит, теория упругости, вид деформированного состояния, вид напряженного состояния, материальные константы, экспериментальные данные, пропорциональное нагружение
Короткий адрес: https://sciup.org/146282036
IDR: 146282036 | УДК: 539.3 | DOI: 10.15593/perm.mech/2021.1.06
Текст научной статьи Определяющие соотношения для материалов со свойствами, зависящими от вида деформированного состояния
ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2021PNRPU MECHANICS BULLETIN
Механические свойства материалов, содержащих дефекты различного характера, трещины, поры, таких как конструкционные графиты, бетон, некоторые горные породы, демонстрируют зависимость от условий нагружения [1, 9, 12, 23, 24, 26, 27]. К такого рода материалам, демонстрирующим зависимость от вида деформированного состояния, также относятся и металлы,
в частности некоторые марки стали, чугуна, меди и алюминия [28–33]. Для подобных материалов характерны следующие свойства [1, 5–7, 13, 26]: отсутствие единой диа-
граммы связи эквивалентного напряжения σ=
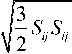
с эквивалентной деформацией
8 =
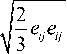
где
S = a j -aS , , a = a i /3 ,
eij = Eij -J85,E = s«,
различие
модуля упругости при растяжении и сжатии, под которым понимаются секущие модули при линейной аппроксимации диаграмм деформирования, зависимость объемных деформаций от сдвиговых.
Такие эффекты можно трактовать как зависимость свойств материалов от вида напряженного (деформированного) состояния. Анализ экспериментальных данных показывает, что наиболее ярко подобная связь проявляется с ростом деформации в нелинейной области деформирования [6]. В работе [10] описываются особен-
ности построения определяющего соотношеня, учитывающего изменение механических свойств горных пород под действием объемного давления. В работе [13] предлагается определяющее соотношение для горных пород, учитывающее зависимость свойств от давления, а также предлагаются экспериментальные методы определения материальных постоянных. В работах [14, 15] исследуется зависимость прочности песчаника от вида напряженного состояния, приводятся результаты одноосных и трехосных испытаний и предлагается соответствующее определяющее соотношение. В работе [16] проводятся исследования пористых горных пород, в частности мела, и предлагается определяющее соотношение, которое проверяется по результатам трехосных испытаний с учетом влажности образцов. В работе [17] исследуются горные породы и предлагается определяющее соотношение, которое описывает эффект уменьшения твердости при увеличении деформации (разупрочнение).
Задача построения определяющих соотношений теории пластичности деформационного типа, учитывающих зависимость от вида напряженного состояния, характеризуемого параметром ^ = a / c0, рассматривается в работе [1]. В упомянутой работе предлагаются соотношения, описывающие зависимость деформации от напряжения. Существует широкий класс задач, в которых постулируется кинематика (представление для перемещений), например задачи плоской деформации. В таких задачах (исходя из соответствующих предпо-
ложений) считается известной форма представления поля перемещений. В таком случае автоматически удовлетворяются уравнения совместности деформаций. Для решения этого класса задач требуется найти обратное определяющее соотношение, описывающее зависимость напряжений от деформации. Аналитический вывод соотношения, обратного рассматриваемому в работе [1], является достаточно трудоемкой задачей и возможен только в случае некоторых упрощений [2].
В данной работе используется методика построения модели материала, описывающей зависимость напряжения от деформации с учетом вида напряженного состояния на основании обработки результатов механических испытаний. Несмотря на то что сегодня интерес специалистов направлен преимущественно на изучение более общих теорий пластичности, например теории пластического течения [14–22, 25], деформационная теория сохраняет свою актуальность при исследовании поведения материалов в условиях пропорционального нагружения [8].
В [1] предлагается потенциал деформаций, имеющий вид
Ф = Ф(^, O ) = 1 ( A + B ^ )O +(1 + к(^)) g (O0 ) ,
2 ( 1 + v ) В - 3(1 — 2 V ) 3 E ’ E
Здесь первое слагаемое соответствует линейноупругому потенциалу, функция g ( ст„ ) характеризует нелинейность диаграмм деформирования и обычно аппроксимируется степенной функцией g (о0) = к о n / n , а функция к ( ^ ) - зависимость диаграмм деформирования от вида напряженного состояния.
Из потенциала такого вида выведем соотношения между деформациями и напряжениями:
б “=!Ф = 3 (A + Х® к о-2) Sj ++1 (B + Л(£) к O-2 )о5 j, (1)
Х = 1 -к,-, "''-'-, Л(^) = к' (^) / (^n).
n
Отсюда можно выразить связь между эквивалентными напряжениями и деформациями, а также между сверткой тензоров напряжений и деформаций:
б = ( B + Л(£) к On-2 )о,Б0 =(A +х(^)kо0-2 )°0-
В случае n = 2, соответствующем прямолинейным диаграммам деформирования, а также для линейной функции вида напряженного состояния к(^) = 2C^-1, где С – параметр вида напряженного состояния, данное определяющее соотношение обращается следующим образом [2]:
о j
2 ( B - C y ) e j + ( A - C / y ) e5 „ AB - CC
где у = б / б0 - параметр вида деформированного со- стояния.
Нахождение точного определяющего соотношения, обратного (1), при нелинейности диаграмм деформирования ( n ^ 2) приводит к слишком громоздким выкладкам и возможно только приближенно (в рядах). Для такого обращения должен быть заранее выбран вид функции к ( ^ ) , что приведет к потере общности. В основе всякой математической модели материала должны быть экспериментальные данные. Любым механическим испытаниям свойственно наличие погрешностей, связанных с неидеальностью материала, невозможностью получения абсолютно идентичных образцов. Эти свойства в особой мере присущи материалам из рассматриваемого класса, например горным породам. Следовательно, наличие громоздкого и неудобного, но «точного» обратного соотношения для большей части его возможных применений нецелесообразно. Более простым представляется построение «обратного» определяющего соотношения, по возможности перенимающего свойства и качества исходного на базе результатов испытаний. Для такого определяющего соотношения константы материала можно найти непосредственно из экспериментальных данных без необходимости их специального пересчета (напомним, что аналитическое представление обратной функции от (1) выражено в рядах), что в некоторых случаях может оказаться удобнее.
При построении теории исходим из следующих гипотез:
-
• Существует потенциал соотношения между на
пряжениями и деформациями.
-
• Деформации считаются малыми.
-
• Учитывается зависимость потенциала только от
первого инварианта деформаций и интенсивности деформаций, что позволит нам охарактеризовать деформированное состояние в среднем. Зависимостью от параметра Надаи-Лоде возможно пренебречь [1, 6, 12, 11], поскольку между тремя главными инвариантами деформаций, характеризующими деформированное состояние, существует только два связывающих их независимых соотношения, и нам будет достаточно ε и ε0. Таким образом, искомые определяющие соотношения остаются тензорно-линейными (но при этом сохраняется возможность описывать поведение «физически нелинейной» среды).
-
• Определяющие соотношения включают, как частные случаи, соотношения нелинейной теории упругости и закон Гука.
Для общности можно перейти от параметра вида напряженного состояния к параметру вида деформиро- ванного состояния и затем рассматривать вместо потенциала деформаций U(е0, у) потенциал U(е, е0) .
Определяющие соотношения и экспериментальные данные
Потенциальная функция деформационых соотношений может быть выбрана в следующем виде:
U = U ( е , £ 0 ) = c s£ o + f ( е ) + g (е0 ) . (3)
Тогда в случае c
= 0, f ( е ) = AL , g ( е о ) = BL из (3)
получим закон Гука.
Из формы представления потенциальной функции (3) непосредственно следует наличие зависимостей между инвариантами напряжений и деформаций:
_ d U ( е , е о )_д U ( е , е о ) де д U ( е , е о ) де0 _ j‘ ' де у де де у + де о де у
= dU(е,ео)g +дЦ(£,£о) 2 ej де 8 де0 3 е0 ’
Пу =(Сео + f (е))3у+т—(Се + g (ео)), 3 ео п = c £о + f '(е), По = С£ + g'(£о ).
Суть дальнейшей работы сводится к следующему: необходимо подобрать экспериментальные данные, позволяющие в каждый момент эксперимента получать значения п, п0 , е , е0; затем по таким экспериментальным данным с помощью методов регрессионного анализа строятся «поверхности» вида п = п( £ , е0 ) , п0 = п0 ( е , е0 ) , которые аппроксимируются функциями вида (4).
Указанным критериям соответствуют экспериментальные данные, опубликованные в работе [3]. В ней приводятся результаты испытаний различных горных пород, проведенных на установке пропорционального нагружения. Полученные в опытах деформации малы, поэтому можно считать, что для описания поведения материала применимы потенциальные соотношения нелинейной теории упругости.
Исследования выполнялись в условиях объемного напряженного состояния при п > п: = п3 .
На основании анализа экспериментальных данных примем:
-
2 k + 1 + 1
f (е) = b£-, g (£о ) = е^, ы ы( A e£ k+1 b£2
U = U ( £ , £ о ) = С ££ о + j^j + — ,
£=£А , £ - =\| 3 e - e - , e - =£ - - 3 е5 --
Таким образом, определяющие соотношения (4) примут следующий вид:
f2 ^ I кС£ I fС£0
П- =lol6v\<2ik0 +— | + е§у — + b ,
V 3 V V е^)V £ J
П = Се + ее k,(6)
п = Ье + С£о.(7)
Сравним (5) с определяющим соотношением (2), являющимся частным случаем общего определяющего соотношения (1) [1, 2], в результате находим, что
21 C£ I I
-I ВIm- +I Al
-
3 V £0 V Vе V
П„ =-------------------э------------ i АВ - CC
.
С точностью до переобозначения констант, данное соотношение совпадает с (5) при k = 1.
Достаточным условием единственности решения краевой задачи является выпуклость потенциала [3]:
ЗиуЗе у> О, где
+ 5е о
2 e
5п у
§ £ у =5 е у + 1 8 £ 5 у ,
. к - 2
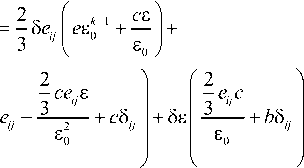
V
Воспользовавшись тем, что свертка симметричного и антисимметричного тензора равна нулю, а также свойствами
2 2 2
- еу 5еу =£О 5ео, -5еу. 5еу >(5ео ) , получим
5пу5£у > -1 (f15£o + f,5е)2 +fb-f2^ |(5£)2, где f = ek£0-1, f, = с.
Тогда условия единственности можно сформулировать следующим образом:
ek е k-1 > О, b —c— ek £ k
> О.
Также для единственности решения краевой задачи необходима положительность энергии деформации:
k + 1
- Ь£2 + C££„+ —0- > 0.
-
2 0 k + 1
Для определяющих соотношений (5) найдем константы материала для некоторых горных пород, воспользовавшись методом наименьших квадратов. Результаты приведены в табл. 1.
Таблица 1
Результаты обработки экспериментальных данных
Table 1
Results of experimental data analysis
|
Порода |
e , МПа |
c , МПа |
k |
b , МПа |
|
Талькохлорит |
5961 |
–6000 |
0,6644 |
33 590 |
|
Известняк |
846 |
–5000 |
0,4464 |
5738 |
Полученные постоянные материала удовлетворяют условиям единственности для всех рассмотренных в экспериментах комбинаций первого инварианта деформаций и интенсивности деформаций. На рис. 1, 2 представлены результаты сопоставления экспериментальных данных с теоретическими зависимостями для талькохлорита и известняка. Маркерами обозначены экспериментальные точки, сплошными линиями – отклик математической модели на соответствующую программу нагружения.
В большинстве экспериментальных результатов, анализируемых в статье, условия соответствовали пропорциональности изменения главных напряжений.
В случае рассматриваемых ниже экспериментов по испытанию бетона одно из главных значений тензора напряжений равнялось нулю, так что условие пропорциональности выполнялось для напряжений в плоскости. Для каждого вида испытаний можно получить зависимость между объемной деформацией и интенсивностью деформации. Несмотря на линейную зависимость гидростатической компоненты напряжений и интенсивности напряжений от первого инварианта тензора деформаций в соотношениях (6) и (7), зависимость £ ( £0 ) нелинейная и определяется свойствами материала и программой эксперимента. Данная зависимость оказывает влияние на вид представленных ниже графиков (рис. 1–5).
Результаты сравнения показывают, что предлагаемое определяющее соотношение с удовлетворительной точностью описывает поведение талькохлорита при испытаниях на пропорциональное нагружение практически во всем диапазоне изменения напряжений. Максимальное относительное отклонение теоретических значений инвариантов напряжения от экспериментальных не превышает 20 %. Для известняка соответствие экспериментальных данных с моделью хуже: максимальное отклонение для значений ст0 составляет 20 %, а для значений ст - несколько выше. При оценке качества модели следует учитывать, что разброс первичных экспериментальных данных для горных пород может достигать 20 %.
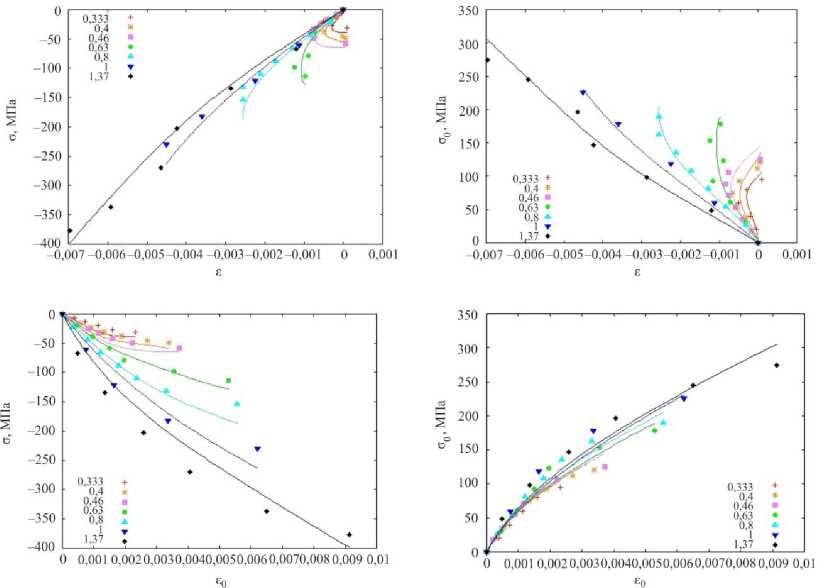
Рис. 1. Сопоставление экспериментальных данных испытаний талькохлорита с расчетными для различных значений параметра вида напряженного состояния ст / ст0
Fig. 1. Comparison of experimental data of talcochlorite tests with calculated data for different values of the stress state type parameter ст / ст0
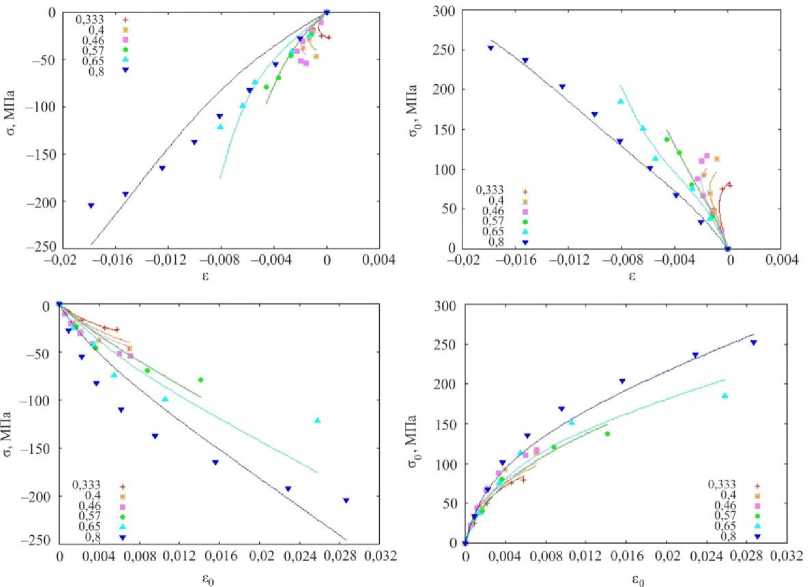
Рис. 2. Сопоставление экспериментальных данных испытаний известняка с расчетными для различных значений параметра вида напряженного состояния ст / ст0
Fig. 2. Comparison of experimental data of limestone tests with calculated data for different values of the stress state type parameter ст / ст0
Испытания бетона в условиях двухосного нагружения проводятся уже на протяжении более чем 100 лет. Целью экспериментаторов, как правило, является определение критериев прочности бетона различных марок. В некоторых работах приводятся графики, описывающие процесс деформирования образцов. Следует отметить существенный разброс в результатах испытаний, проводимых различными авторами. В частности, значения прочности для двухосного сжатия могут отличаться в 4 раза [27].
Воспользуемся результатами экспериментов на двухосное пропорциональное нагружение, приведенными в [27]. Испытывался бетон марки М-300 (табл. 2, рис. 3). В состав бетона входил гравий, с максимальным диаметром частиц наполнителя 15 мм. Соотношение между водой и цементом 0,9, объемное содержание цемента в растворе – 190 кг/м3. Образцы заливали в горизонтальные металлические формы с точной геометрией, вручную уплотняли, выдерживали во влажной среде в течение 7 дней и затем оставляли в помещении с относительной влажностью 68 % и температурой 20 °С на 21 день.
Эксперимент осуществлялся в специально изготовленной испытательной машине для двухосного нагружения. Усилие на образцы передавалось через стальные плиты, причем поверхность плит, контактирующая с бетоном, имела частые глубокие канавки, так что плита представляла собой «щетку». Такая форма плит обеспечивала уменьшение трения между ней и испытываемым образцом. Двухосное нагружение обеспечивалось гид-равличесикими цилиндрами с максимальным усилием сжатия в 75 т и максимальным усилием растяжения в 40 т. Постоянство соотношения главных напряжений обеспечивалось с помощью специального гидравлического распределительного устройства. Для испытаний на растяжение образцы бетона склеивались с нагрузочными плитами с помощью эпоксидного клея.
Результаты данных испытаний также были обработаны способом, описанным выше. Были определены постоянные материальной функции. Результаты сопоставления экспериментальных данных с расчетными представлены на рис. 6. Некоторая «волнистость» полученных диаграмм связана с погрешностями оцифровки графиков из статьи. Следует отметить, что возникающая в связи с этим ошибка по порядку величины меньше, чем разброс экспериментальных данных испытаний бетона, который может составлять порядка 10–20 %.
Таблица 2
Результаты обработки экспериментальных данных для бетона
Table 2
Results of experimental data analysis for concrete
|
Марка бетона |
e , МПа |
c , МПа |
k |
b , МПа |
|
Бетон М-300 |
166,8 |
–3790 |
0,38 |
7601 |
|
Бетон HSLW М-700 |
12 520 |
–1446 |
0,8725 |
24 070 |
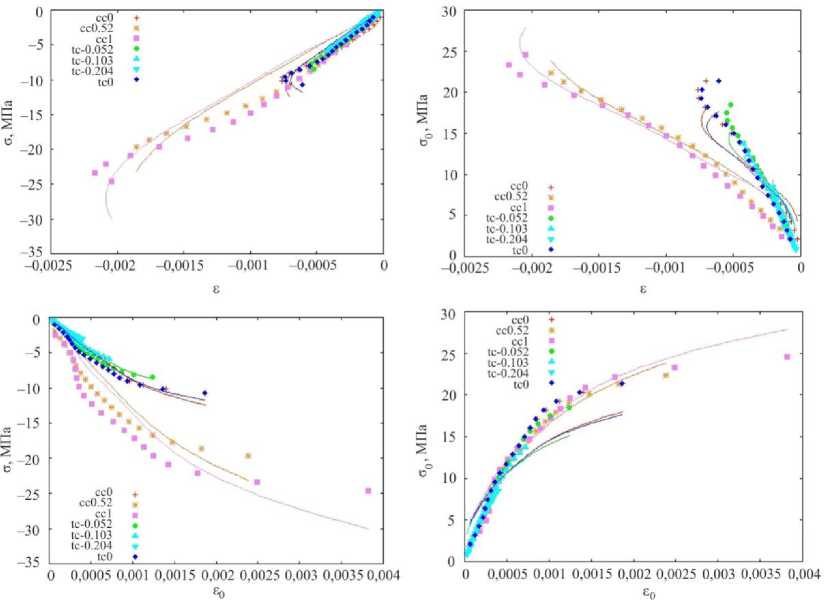
Рис. 3. Сопоставление экспериментальных данных испытаний бетона М-300 с расчетными для различных соотношений ст, / ст2 для сжатия по двум осям (cc) и для сжатия с растяжением (tc). Точками отмечены результаты испытаний, сплошными линиями – модель
Fig. 3. Comparison of experimental test data for M-300 concrete with calculated data for different ratios of ст, / ст2 for compression along two axes (cc) and for compression with tension (tc). The test results are marked with dots, and the model is marked with solid lines
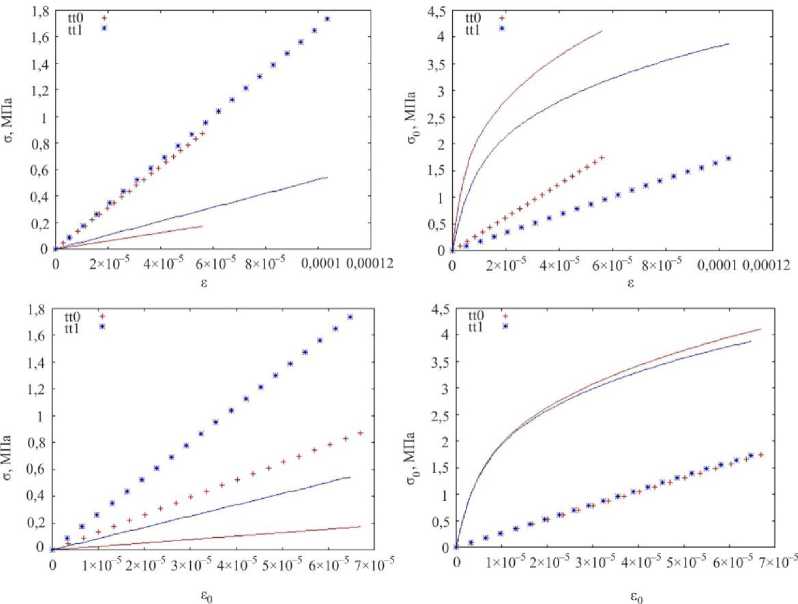
Рис. 4. Сопоставление экспериментальных данных испытаний бетона М-300 с расчетными для различных соотношений ст, / ст2 для растяжения по двум осям (tt). Точками отмечены результаты испытаний, сплошными линиями – модель
Fig. 4. Comparison of experimental test data for M-300 concrete with calculated data for different ratios of ст, / ст2 for two-axis tension (tt). The test results are marked with dots, and the model is marked with solid lines
Соответствие модели результатам испытаний несколько хуже, чем в случае горных пород. Для двухосного сжатия и сжатия с растяжением относительное отклонение экспериментальных значений σ от теоретических не превышает 25 %, для σ – 20 %. Следует отметить неприменимость предлагаемой модели для описания двухосного растяжения.
В работе [26] описываются аналогичные испытания по двухосному нагружению различных марок бетона. Были обработаны результаты исследований механического поведения образцов высокопрочного легковесного бетона (HSLWC) марки М-700 (см. табл. 2, рис. 4). Состав смеси на 0,1 м³ бетона: 40 кг цемента, 3,4 кг микрокремнезема, 61 кг мелкого заполнителя, 67 кг крупного заполнителя, 75 мл замедлителя схватывания бетона, 1000 мл суперпластификатора. Плотность смеси составила 1950 кг/м3. Бетон заливали в плексигласовые формы, уплотнение обеспечивалось помещением форм на 60 с на вибрирующий с частотой 40 Гц стол. После затвердевания образцы накрывали пластиковыми крышками, чтобы избежать высыхания. Через два дня после затвердевания образцы вынимали из форм и помещали в резурвуар с чистой водой на 56 дней. Затем образцы помещали в комнату с относи- тельной влажностью 99 % и постоянной температурой 20 °С. За два дня до испытаний образцы извлекали из комнаты, после чего их поверхности шлифовались алмазным диском для обеспечения необходимой точности геометрии.
Конструкция испытательной машины и нагрузочных плит аналогична описанной выше. Двухосное нагружение обеспечивалось линейными актуаторами с сервоприводами с обратной связью, обеспечивающими максимальное усилие в 710 кН. Поверхностные деформации на плоскостях образцов, контактирующих с нагрузочными плитами, измерялись с помощью экстензометров, приклеенных к образцам с помощью эпоксидного клея, деформации в направлении действия сил и деформация на свободной поверхности измерялись с помощью высокоточных LVDT-датчиков.
Для двухосного сжатия и сжатия с растяжением относительное расхождение между экспериментальными значениями σ и теоретическими не превышает 10 %, для σ – 15 %.
Для условий растяжения максимальное относительное различие между экспериментальными и теоретическими значениями для σ не превышает 20 %, для σ отклонение несколько больше.
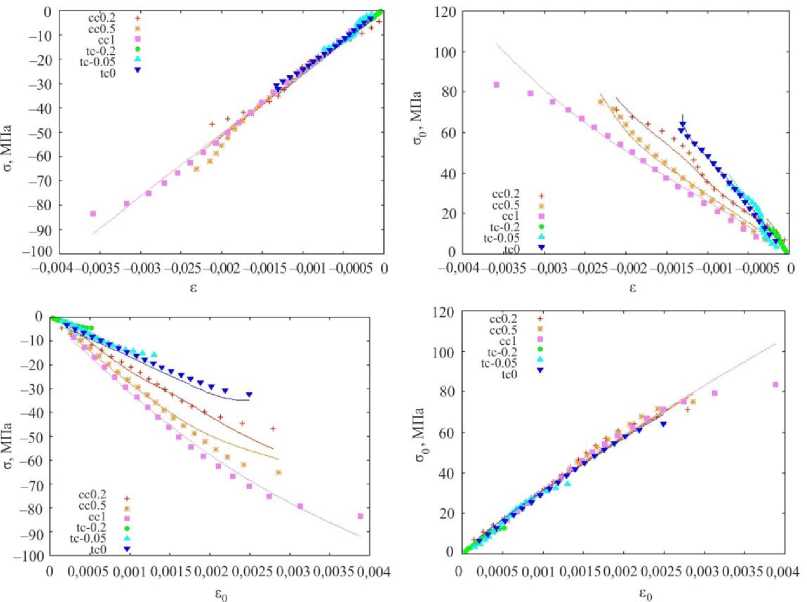
Рис. 5. Сопоставление экспериментальных данных испытаний бетона HSLW М-700 с расчетными для различных соотношений σ/σ для сжатия по двум осям (cc) и для сжатия с растяжением (tc). Точками отмечены результаты испытаний, сплошными линиями – теоретические зависимости
Fig. 5. Comparison of experimental test data for HLSW M-700 concrete with calculated data for various ratios of σ/σ for compression along two axes (cc) and for compression with tension (tc). Test results are marked with dots, and theoretical dependencies are marked with solid lines
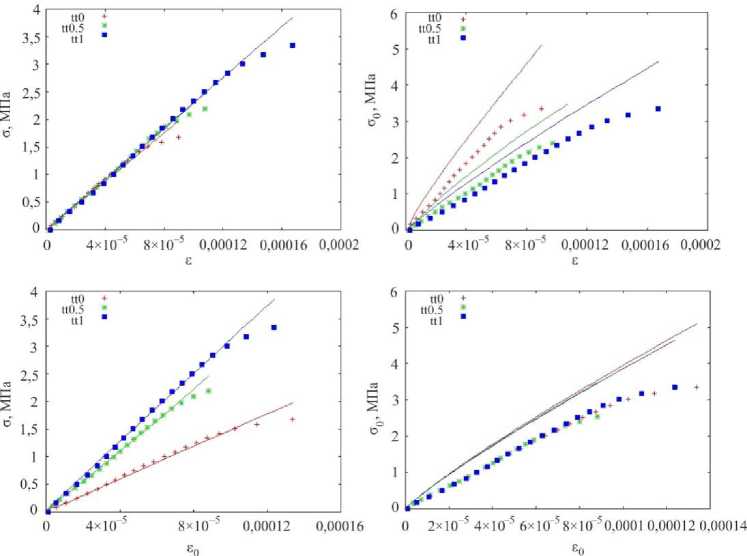
Рис. 6. Сопоставление экспериментальных данных испытаний бетона HSLW М-700 с расчетными для различных соотношений а, /а2 для растяжение по двум осям (tt). Точками отмечены результаты испытаний, сплошными линиями - модель
Fig. 6. Comparison of experimental test data for HLSW M-700 concrete with calculated data for different ratios of а, /a2 for two-axis tension (tt). The test results are marked with dots, and the model is marked with solid lines
Различные образцы бетона, как и рассмотренные горные породы, демонстрируют зависимость своих механических свойств от вида напряженного состояния. Особенно существенно от вида напряженного состояния зависит предел прочности. Требуется проведение дальнейших исследований для обоснования применимости определяющих соотношений вида (5).
Заключение
Предлагаемые определяющие соотношения учитывают зависимость механических свойств от вида напряженного (деформированного) состояния. Определяющие со- отношения такого типа могут быть полезны для описания механического поведения широкого класса материалов, например металлов, горных пород, пластиков. В данной работе выведены условия на материальные параметры определяющего соотношения, обеспечивающие единственность решения краевой задачи. С помощью методов регрессионного анализа обработаны результаты испытаний на сложное нагружение различных горных пород и марок бетона, определены значения механических характеристик. Установлена ограниченная применимость предлагаемого определяющего соотношения. Найдено относительное отклонение между экспериментальными данными и результатами, предсказываемыми моделью.
Список литературы Определяющие соотношения для материалов со свойствами, зависящими от вида деформированного состояния
- Ломакин Е.В. Определяющие соотношения деформационной теории для дилатирующих сред // Изв. АН СССР. Механика твердого тела. - 1991. - № 6. - С. 66-75.
- Ломакин Е.В. Кручение цилиндрических тел с изменяющимися деформационными свойствами // Изв РАН. Механика твердого тела. - 2008. - № 3. - С. 217-226.
- Ломакин Е.В. О единственности решения задач теории упругости для изотропного разномодульного тела // Изв. АН СССР. Механика твердого тела - 1979. - № 2. - С. 42-45.
- Ставрогин А.Н., Протосеня А.Г. Пластичность горных пород. - М.:Недра, 1979. - 301 с.
- Ломакин Е.В. Нелинейная деформация материалов, сопротивление которых зависит от вида напряженного состояния // Изв. АН СССР. Механика твердого тела. - 1980. -№ 4. - С. 92-99.
- Ломакин Е.В. Зависимость предельного состояния композитных и полимерных материалов от вида напряженного состояния. Ч. I Экспериментальные зависимости и определяющие соотношения // Механика композитных материалов. -1988. - № 1. - С. 3-9.
- Ломакин Е.В. Разномодульность композитных материалов // Механика композитных материалов. - 1981. - № 1 -С. 23-29.
- Jones R.M. Deformation Theory of Plasticity. - Bull Ridge Pub, 2009. - 640 p.
- Николаевский В.Н. Современные проблемы механики грунтов // Определяющие законы механики грунтов. Механика. Новое в зарубежной науке. - М.: Мир, 1975. - С. 210-229.
- Rudnicki J.W., Rice J.R. Conditions for the localization of deformation in pressure-sensitive deviant materials // J. Mech. Phys. Solids. - 1975. - Vol. 23, no. 6. - Р. 371-394. DOI: 10.1016/0022-5096(75)90001-0
- Новожилов В.В. О физическом смысле инвариантов, используемых в теории пластичности // ПММ. - 1952. - Т. 16, вып. 5. - С. 615-619.
- Белякова Т.А., Ломакин Е.В. Упругопластическое деформирование дилатирующей среды вблизи вершины трещины в условиях плоского напряженного состояния // Изв. РАН. Механика твердого тела. - 2004. - № 1. - С. 109-118.
- Desai C.S., Salami M.R. A constitutive model and associated testing for soft rock // Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. - 1987. - No 24. - Р. 299-307. DOI: 10.1016/0148-9062(87)90866-7
- Khan A.S., Xiang Y., Huang S. Behavior of Berea sandstone under confining pressure part I: yield and failure surfaces, and nonlinear elastic response // Int. J. plasticity. - 1991 - Vol. 7, no. 6. - P. 607-624. DOI: 10.1016/0749-6419(91)90046-2
- Khan A.S., Xiang Y., Huang S. Behavior of Berea sandstone under confining pressure part II: elastic-plastic response // Int. J. plasticity. - 1992 - Vol. 8, no. 3. - P. 209-220. DOI: 10.1016/0749-6419(92)90048-H
- Shao J.F., Henry J.P. Development of an elastoplastic model for porous rock // Int. J. plasticity. - 1991. - Vol. 7, no. 1. -P. 1-13. DOI: 10.1016/0749-6419(91)90002-G
- Adachi T., Oka F. An elasto-plastic constitutive model for soft rock with strain softening // Int. J. Numer. Anal. Methods Geomechanics. - 1995. - No. 19. - P. 233-247. DOI: 10.1016/S1003-6326(16)64173-0
- Nova R. A Simple Elastoplastic Model for Soils and Soft Rocks // Soil Constitutive Models American Society of Civil Engineers. - 2005. - P. 380-399. DOI: 10.1061/40771(169)16
- A micro-macro model for clayey rocks with a plastic compressible porous matrix / W.Q. Shen, J.F. Shao, D. Kondo, B. Gatmiri // Int. J. Plasticity. - 2012. - No. 36 - P. 64-85. DOI: 10.1016/j.ijplas.2012.03.006
- Shen W.Q., Shao J.F. An incremental micro-macro model for porous geomaterials with double porosity and inclusion // Int. J. Plasticity. - 2016. - No. 83. - P. 37-54. DOI: 10.1016/j.ijplas.2016.04.002
- Multiscale formulation for material failure accounting for cohesive cracks at the macro and micro scales / S. Toro, P.J. Sánchez, P.J. Blanco, E.A. de Souza Neto, A.E. Huespe, R.A. Feijóo // Int. J. Plasticity. - 2016. - No. 76. - P. 75-110. DOI: 10.1016/j.ijplas.2015.07.001
- Zreid I., Kaliske M. An implicit gradient formulation for microplane Drucker-Prager plasticity // Int. J. Plasticity. - 2016. -No. 83. - P. 252-272. DOI: 10.1016/j.ijplas.2016.04.013
- Yoshinaka R., Tran T.V., Osada M. Mechanical behavior of soft rocks under triaxial cyclic loading conditions // International Journal of Rock Mechanics and Mining Sciences - April-June 1997. - Vol. 34, no. 3-4. - P. 354.e1-354.e14. DOI: 10.1016/S1365-1609(97)00243-8
- Yintong Guo, Chunhe Yang, Haijun Mao. Mechanical properties of Jintan mine rock salt under complex stress paths // International Journal of Rock Mechanics and Mining Sciences - December 2012 - Vol. 56. - P. 54-61. DOI: 10.1016/j.ijrmms.2012.07.025
- Peng-Fei Qu Qi-Zhi Zhu, Yi-Fei Sun Elastoplastic modelling of mechanical behavior of rocks with fractional-order plastic flow // International Journal of Mechanical Sciences. - 2019 - Vol. 163, no. 4.134. - P. 105-102. DOI: 10.1016/j.ijmecsci.2019.105102
- Hussein A., Marzouk H. Behavior of High-Strength Concrete under Biaxial Stresses // Aci Structural Journal. - 2000. -Vol. 97. - P. 27-36.
- Kupfer Helmut B., Gerstle Kurt H. Behaviour of concrete under biaxial stresses // ASCE J Eng Mech Div. - 1973. -Vol. 99, no. 4. - P. 853-866.
- Bai Y., Wierzbicki T. A new model of metal plasticity and fracture with pressure and Lode dependence // International Journal of Plasticity. - 2008. - No. 24. - P. 1071-1096. DOI: 10.1016/j.ijplas.2007.09.004
- Development, implementation and validation of 3-D Failure Model for Aluminium 2024 for High Speed Impact Applications / P. Du Bois, M. Buyuk, J. He, S. Kan. // 2nd Russian LS_DYNA Users Conference October 7-8, 2010, Dalnaya Dacha, Russia.
- Ductile damage evolution under triaxial state of stress: theory and experiments / N. Bonora, D. Gentile, A. Pirondi, G. Newaz. // International Journal of Plasticity. - 2005. - No. 21. -P. 981-1007. DOI: 10.1016/j.ijplas.2004.06.003
- Anisotropic failure modes of high-strength aluminium alloy under various stress states / M. Fouremeau, T. Borvik, A. Benallal, O.S. Hopperstad. // International Journal of Plasticity. -2013. - No. 48. - P. 34-53. DOI: 10.1016/j.ijplas.2013.02.004
- Effects of the stress state on plasticity and ductile failure of an aluminium 5083 alloy / X. Gao, T. Zhang, M. Hayden, Ch. Roe // International Journal of Plasticity. - 2009. - No. 25. -P. 2366-2382. DOI: 10.1016/j.ijplas.2009.03.006
- Seidt J.D. Plastic Deformation and Ductile Fracture of 2024-T351 Aluminium under Various Loading Conditions: PhD Thesis. - Ohio State University, 2010.


