Optical properties of lowest-energy carbon allotropes from first-principles calculations

Diamond and different forms of carbon materials are the subject of the intensive theoretical and experimental study [1, 2]. It is well known that carbon can form sp2 and sp3 hybridized bonds which are realized under ambient conditions in cubic diamond, graphite, fullerene and graphene [3]. At high temperature and pressure graphite can be converted to cubic diamond or to the lonsdaleite (2H hexagonal diamond) [4, 5]. For a long time, hexagonal diamond has been produced artificially by static and shock wave compression of well-crystallized graphites [6]. Recently it was shown that hexagonal diamond can be also obtained from cubic diamond [7]. It was found that graphite cold-compression leads to a creation of the new sp3-bonded stable forms of carbon allotropes [8]. Nowadays, there are about two hundreds of different predicted hypothetical sp3 carbon allotropes, which are collected in the SACADA database [9]. The small difference of energy of several these allotropes relatively to the diamond, 0.01–0.10 eV per atom, raises the idea of a possibility to find these allotropes in the mixed carbon phases. The experimental search of such carbon allotropes should be based on some new physical information about formation of these new phases. The most probable signals can be connected with optical properties of the materials, such as Raman spectra, optical coefficients in the regions of infrared (IR), visible and ultraviolet (UV) spectra, as well as the energy dependence of the absorption and refractive indices. Here we calculate different optical properties of the six low-est-energy sp3 carbon allotropes: cubic diamond, lonsdaleite [4], 4H-diamond [10], SiC12 [11], C28 [12] and mtn [13]. The main goal of our study is to find the quantitative level of difference between optical properties of cubic diamond and relevant carbon allotropes, which can be measured experi- mentally. We start with a prediction of Raman shift spectra and IR active mode spectra, than we will study energydependent complex dielectric functions and their derivative in the ranges of visible and ultraviolet light. Our calculations are based on density-functional-theory (DFT) methods [14, 15] as it is implemented in CRYSTAL14 [16] and VASP [17] program packages. The calculations for the IR range have been done using CRYSTAL14 program, which uses the all-electron approach with atomic orbital basis sets. The relevant calculations in the visible and ultraviolet ranges of light have been done using VASP program package which uses plane-wave basis sets and the pseudo-potential approach.

Computational methods and details

Raman and IR spectra of crystal structure are defined by the set of harmonic phonon frequencies at the Γ point which can be obtained from the diagonalization of the Hessian matrix of the second derivatives with respect to atomic displacements [18]:

H ^r. =     ¹

ai , bj      M _a M _b

f d ² E ) b ( ^d u ai ^d u j J

where u ai and u bj are displacements of atoms a and b in the reference cell along the i-th and j-th Cartesian directions, respectively.

The Raman intensity of the Stokes line of a phonon mode Q p , active due to the a у component of the polarizability tensor a , is expressed as follows:

i>4^da у ^{/ d} Q p ) 2 . (1)

The scheme of calculation, recently implemented in the CRYSTAL14 program [16], explores second-order Coupled-

Perturbed Hartree-Fock/Kohn-Sham (CPHF/KS) equations [19]. The Raman spectrum is then computed by considering the transverse optical (TO) modes and by adopting a pseudoVoigt functional form: a linear combination of a Lorentzian and a Gaussian curve with full width at half maximum of 8 cm-1. Raman intensities are normalized so that the largest value is conventionally set to 100 a.u.

To calculate IR spectra we should know the complex dielectric tensor ε ii ( v ) which is computed for each inequivalent polarization direction on the basis of a classical Drude-Lorentz model:

ε ii ( ν ) =ε opt , ii + ∑ f p , ii ν ² p /( ν ² p -ν ² - i νγ p ), (2) ^p

where ii indicates the polarization direction, ε opt,ii is the optical dielectric tensor, v p , f p and γ p are the TO frequency, oscillator strength and damping factor for the p-th vibration mode, respectively. The real and imaginary parts of ε ii ( v ) are computed and the maxima of this function correspond to the TO frequencies. The optical or high-frequency dielectric tensor is computed in a quasi-free electron approximation via coupled perturbed Hartree-Fock (Kone-Sham) method [20]. The refractive (n) and absorption (k) indices are computed as real and imaginary parts of the complex refractive index n ^* ( ν ) = ε , also for

each inequivalent polarization direction.

In the projector augmented plane wave method realized in VASP the frequency-dependent dielectric functions is obtained in the random phase approximation, where the imaginary part of the frequency-dependent dielectric tensor is written as

ε ⁽²⁾ ( ω ) = (4 π ² e ² / Ω )lim(1/ q ² ) ∑ 2 w ×

^{αβ                           q → 0}          c , v , k     ^k

×δ ( ε _ck -ε _vk -ω ) u _{ck + e q} | u _vk V u ck + e q | u vk ck vk ck + e _α q vk ck + e _β q vk ,

where the indices c and v refer to conduction and valence

band states respectively in the sum over the empty states, ε c,vk are the corresponding eigenenergies, Ω is the volume of a primitive cell, k-point weights w k are defined such that they sum to 1, e α , β are the unit vectors for the three Cartesian directions, and u ck is the cell-periodic part of the orbitals at point k. The real part of the dielectric tensor ε ⁽ _α ¹ _β ⁾ ( ω ) is ob-

tained by the Kramers-Kronig transformation

ε(α1β) (ω) =1+π2P∫0∞

ε(αβ)(ω′)ω′

ω′ ²

-

2 . ■ ω +iη

d ω ,

where P denotes the principal value. By cubic symmetry, the following relation is satisfied for diamond and mtn

ε ( _x 1 _x ,2) ₌ε ( _y 1 _y ,2) ₌ε ( _z 1 _z ,2) , ε ( _α 1 _β ,2) ₌ 0, α_≠β ,                    (5)

so the real and imaginary parts of the complex dielectric constant ε = ε1+iε2 can be determined by ε = ε(1,2) . In 1,2 xx the case of the other, anisotropic, structures we use the average values:

ε 1,2 =ε 1,2 = (1/3)( ε ⁽ x ¹ x ^,2) +ε ⁽ y ¹ y ^,2) +ε ⁽ z ¹ z ^,2) ).

Computational setup, CRYSTAL14

We use the two schemes of DFT calculations, both are implemented in the CRYSTAL14 program [16]. The

first one incorporates the Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional [21] at general gradient approximation (GGA) of DFT and POB-TZVP allelectron basis set [22], and the second one – the B3LYP hybrid functional [23] and adopted Pople’s 6-21G Gaussian all-electron basis set [24, 25]. The level of accuracy of calculating the energies of Coulomb and Hartree-Fock exchanges is controlled by a set of TOLINTEG parameters, which were chosen as {8, 8, 8, 8, 18}. The convergence threshold on energy for the self-consistent-field (SCF) calculations is 10–7 Hartree for structural optimization and 10–8 Hartree for vibration frequency calculations. The number of basis vectors in the irreducible Brillouin zone is given by the shrink parameter IS = 8 for structural optimization and IS = 16 for vibration frequency calculations. The relaxation of cell parameters and atomic positions to equilibrium values was carried out until the lattice stress became less than 0.02 GPa.

Computational setup, VASP

The computations of the complex dielectric functions in the visible and ultraviolet regions were performed by the VASP package [17] at the level of GGA and with two functionals: the above-mentioned PBE [21] and the screened Heyd, Scuseria, and Ernzerhof (HSE06) hybrid functional [26], since the latter is well-suited to reproduce the electronic properties including the band gaps of a number of elemental and binary insulators and semiconductors. For this purpose, at first we performed the relaxation of the discussed structures with a cutoff energy of 700 eV for the plane-wave basis set, until the energy was converged up 10–7 eV per unit cell and the residual stress was less than 10–5 eV per atom. The integration over the Brillouin zone was performed using Monkhorst-Pack grids with the number of k-points along each direction of the reciprocal cell equal to an integer divisor of 25Å over the length of corresponding lattice vector. The chosen set of input parameters gives the reliable results for the main physical properties of diamond as it was shown in our previous work [12].

Structural properties

The full geometry optimization of studied structures have been performed using the quasi-Newton algorithm in CRYSTAL14 program. The relaxed lattice constants and atomic Wyckoff positions are presented in the Tables 6 and 7. The differences between lattice constants obtained in two schemes of calculations are about 1 %. While the energy differences per atom relatively diamond are equal, see Tables 1 and 2. To check a mechanical stability of hypothetical allotropes under study, we calculated the elastic constants and phonon spectra which are collected in the Fig. 4. Our results for structural properties agree with previous DFT calculations [10 – 13].

Raman and IR spectra

Raman identification of new carbon allotropes needs a precise calculation of vibration spectra. We performed these calculations applying quasi-harmonic approximation at the Г point as it was done for Raman identification of

lonsdaleite in Refs. [27, 28] and for Raman spectroscopy of nanocrystalline diamond in Ref. [29]. We have found for cubic diamond that the position of single Raman peak, corresponding to the first-order scattering of F 2g symmetry, is 1297 cm^–1 (PBE, POB-TZVP ) and 1332 cm^–1 (B3LYP, 6-21G). The last one is in a best agreement with experimental value. Such a way, we perform calculations of Raman and IR spectra here and after using B3LYP exchangecorrelation functional and modified Pople’s 6–21 basis set [25]. The presented in Fig. 1 polycrystalline (powder) Raman spectra were computed by averaging over the all possible orientations of the crystallites.

Table 1. Energy difference per atom relatively diamond, density and bulk modulus of the allotrope (PBE, POB-TZVP)

Structure	ΔE/atom, eV	ρ, g/cm3	B, GPa
diamond	0.00	3.51	443
4H-diamond	0.01	3.61	445
SiC12	0.01	3.53	444
lonsdaleite	0.03	3.51	445
C28	0.07	3.35	427
mtn	0.11	3.06	383

Table 2. Energy difference per atom relatively diamond, density and bulk modulus of the allotrope (B3LYP, 6-21G)

Structure	ΔE/atom, eV	ρ, g/cm3	B, GPa
diamond	0.00	3.43	428
4H-diamond	0.01	3.53	429
SiC12	0.01	3.43	428
lonsdaleite	0.03	3.43	429
C28	0.07	3.37	413
mtn	0.08	2.98	371

For the lonsdaleite we predict three Raman active modes: E 1g (1336), A 1g (1312) and E 2g (1209). Up to now, the pure monocrystalline lonsdaleite have not been found or synthesized and there is a well-known problem of correct diagnostics of lonsdaleite phase within cubic diamond-lonsdaleite intergrowths. Possible attendance of nanocrystalline cubic diamond can be a reason of incorrect interpretation of Raman spectra in experimental study. It was found that the Raman modes dynamics under laser heating allows splitting of cubic diamond and lonsdaleite modes and recognize diamond polymorphs [28]. The measurements in the region of 1300 – 1340 cm^–1 show the presence of two Raman active modes, A 1g (1319) and F 1g (1322). The control measurement for co-sized cubic diamond particles give downshift of a Raman active mode F 2g (1332) up to 1326 cm^–1. Taking into account this downshift effect, we can declare the agreement of our prediction with the experimental data for lonsdaleite [28] at least for two high-frequency modes. We also obtain a rough agreement with recent measurements of Ref. [29], in which the most intensive band at 1292 – 1303 cm^–1 and at 1219-1244 cm^–1 are interpreted as contributions from A 1g and E 2g vibration modes of lonsdaleite phase in Pop-igai impact rock. Early DFT calculations, performed in the local density approximation (LDA), gave the following results: E 1g (1312), A 1g (1305), E 2g (1193) [30] and E 1g (1338), A 1g (1280), E 2g (1221) [31].

In Fig. 1 a – e , we present our results for polycrystalline (powder) Raman spectra with intensity plotted in arbitrary units. Of course, it has the dependence on direction for monocrystalline structures, but it is small and we discuss it later for real refractive indices only. The single peak of cubic diamond corresponding F 2g (1332) mode is shown in all figures for comparison.

The number of active Raman modes or peaks depends on symmetry of crystal lattice and on the number of nonequivalent atoms in the asymmetric unit. As we see, quantum-mechanical approach predicts a very specific Raman spectrum for every allotrope, which can be considered as “finger prints” of these structures in the experimental search. The improvement of experimental methods to the level of accuracy of theoretical calculations will be crucial for search and recognition of diamond polymorphs.

The high-frequency refractive indices n ii for different direction ( ii = xx , yy , zz ), accordingly Voigt notation, are collected in the Table 3. The calculation with PBE functional and POB-TZVP basis set gives answer which is very close to the experimental value for cubic diamond (~2.40) instead of the calculation with B3LYP functional used successfully for Raman spectrum calculation. The refractive asymmetry factor can be defined as follows A ij = 2( n ii – n jj ) / ( n ii + n jj ). The values of A ij for lonsdaleite, C28, sic12 and 4H-diamond are about 2.5–3.5 %. This is enough large values for experimental test and recognition. The list of calculated IR active modes which initiate absorption of light in IR region are presented in Table 4. The ideal cubic diamond and lonsdaleite crystals do not absorb IR light. It means that experimental viewing of absorption for diamond-like structures may be used for recognition of new sp³ carbon allotropes.

Table 3. High-frequency refractive indices along the different directions

Basis set Structure	POB-TZVP, PBE n xx, n yy, n zz	Pople-6-21G, B3LYP n xx, n yy, n zz
Diamond	2.40, 2.40, 2.40	2.34, 2.34, 2.34
lonsdaleite	2.36, 2.36, 2.44	2.30, 2.30, 2.36
Mtn	2.11, 2.11, 2.11	2.10, 2.10, 2.10
SiC12	2.38, 2.38, 2.42	2.32, 2.32, 2.36
C28	2.35, 2.38, 2.43	2.29, 2.32, 2.36
4H-diamond	2.37, 2.37, 2.43	2.32, 2.32, 2.34

Table 4. IR active modes

Basis set Structure	Pople-6-21G, B3LYP
SiC12	E u (425), E u (578), A 2u (728), A 2u (1075), E u (1271),A 2u (1330)
4H-diamond	E 1u (1248), A 2u (1316)
C28	B 2u (443), B 2u (539), B 3u (547), B 1u (586), B 1u (719), B 3u (742), B 2u (786), B 2u (862), B 3u (878), B 2u (962), B 3u (1000), B 2u (1002), B 1u (1071), B 3u (1074), B 3u (1172), B 3u (1203), B 2u (1211), B 1u (1220), B 2u (1239), B 1u (1260), B 2u (1278), B 3u (1279), B 3u (1298), B 3u (1352), B 2u (1356), B 2u (1400)
mtn	F 1u (735), F 1u (871), F 1u (891), F 1u (1059), F 1u (1144), F 1u (1223),

c)

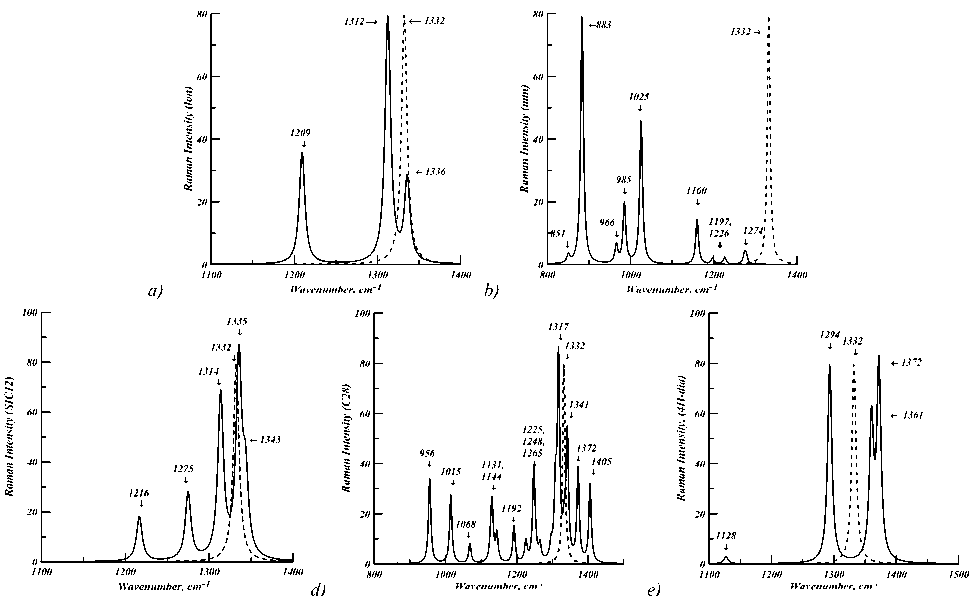
Fig. 1. Raman shift spectra in arbitrary units for carbon allotropes: a) lonsdaleite, b) mtn, c) SiC12, d) C28, e) 4H-diamond. The peak at the 1332 cm–1 in all panels corresponds cubic diamond

Optical and UV spectra

Optical properties are immediately connected with the electronic band structure of the crystal. To calculate the interband and intraband electron optical transitions one needs to solve the band structure of the system and know its band gap in different symmetry points of reciprocal space. Because of this reason, we calculated the electronic band structure for all the allotropes under study (see Fig. 5) and collected to the table our results for indirect and direct (in Г– point) band gaps for all the considered structures within PBE and HSE06 functionals (see Table 5). It is well-known that the former fails to reproduce the optical band gaps while the latter provides the reliable results. Our result of 5.38 eV band gap for diamond successfully reproduces the well-known experimental value of 5.47 eV [1].

Then, we calculated the complex dielectric function for diamond, lonsdaleite and considered lowest-energy allotropes in the random phase approximation as it was explained in the Sec. “Computational methods and Details”. In the Figs. 2 and 3 we present our predictions for diamond obtained with PBE exchange-correlation functional (bold solid line) and HSE06 functional (dashed line) together with experimental data (solid line) from the work [1] and PBE based predictions for lonsdaleite (dash-dotted line). We find a good agreement between theory and experiment within PBE functional calculations in the position and highness of the peaks, while with the HSE06 functional calculations, although providing correct optical band gaps, leads to the shift of the peaks approximately to 1 eV towards the high frequencies. Also, our results for cubic diamond and lonsdaleite are consistent with the earlier calculations in the work [32].

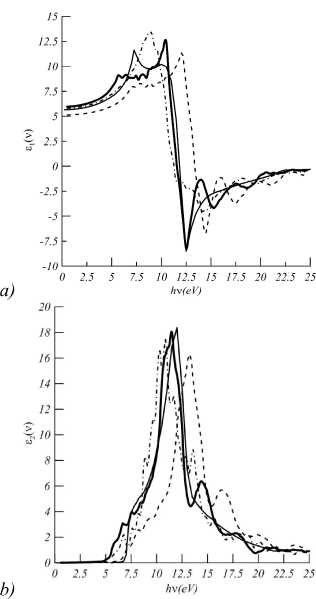
Fig. 2. Real (a) and imaginary (b) dielectric functions: solid line – experiment for cubic diamond, bold solid line – predictions for cubic diamond in PBE, dashed line – predictions for cubic diamond in HSE, dash-dotted line – lonsdaleite in PBE

strate the very similar behavior of ε 1,2 ( v ) to diamond or loncdaleite in the optical and UV region, so they do not lose the desirable optical parameters of diamond. In contrast, the mtn shows 2 times shorter and the smoothest peaks and has the smallest band gap in comparison to other allotropes, but the position of the peaks remains the same. Such a way, a presence of mtn in the polycrystalline sample can contribute a visual opacity.

The effect of the anisotropy of the optical properties for non-cubic structures is found to be small, so we do not show the dependence of the dielectric tensor from the crystal directions in the figures, but only the average values as defined by formula (2.6).

Table 5. Band gaps for carbon allotropes

Structure	PBE, indirect	HSE06, indirect	PBE, direct	HSE06, direct
diamond	4.67	5.38	5.64	7.04
lonsdaleite	3.34	4.91	4.96	6.37
mtn	3.76	5.09	3.76	5.03
Sic21	4.44	5.64	5.25	6.65
C28	4.77	5.96	4.77	6.06
4H-diamond	4.53	5.73	5.29	6.68

Conclusion

In summary, the first-principles quantum-mechanical calculations have been performed to obtain the frequency spectra and optical properties of lowest-energy sp3 carbon allotropes, such as: cubic diamond, lonsdaleite, SiC12, 4H-diamond, C28 and mtn. We have obtained Raman and IR spectra for all discussed allotropes and study their peculiarities. The electronic structure as well as the linear photon energy-dependent complex dielectric functions and related optical properties were computed.

Our investigations are beneficial to the experimental search and to the practical applications of these hypothetic carbon allotropes in IR, visible and UV photonics [33, 34].

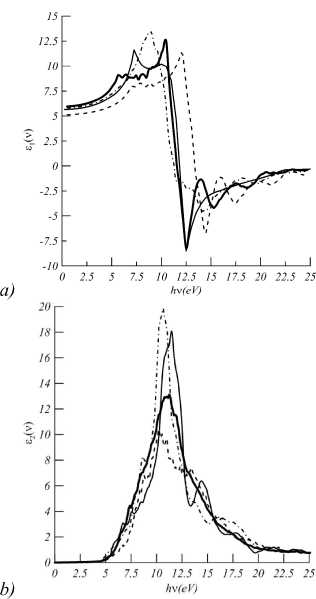
Fig. 3. Real (a) and imaginary (b) dielectric functions in predicted for carbon allotropes in PBE: solid line – cubic diamond, bold solid line – C28, dashed line –mtn, dash-dotted line – SiC12

Table 6. Lattice parameters for carbon allotropes calculated with POB-TZVP basis set and PBE exchange-correlation functional

Structure	N	a, Å	b, Å	c, Å	Atomic positions
diamond	227	3.569	-	-	(0.125, 0.125, 0.125)
lonsdaleite	194	2.507	-	4.169	(0.333, 0.667, 0.062)
mtn	227	9.625	-	-	(0.880, 0.067, 0.683), (0.125, 0.125, 0.625) (0.033, 0.033, 0.716)
SiC12	166	2.511	-	24.822	(0.667, 0.333, 0.740), (0.667, 0.333, 0.572) (0.667, 0.333, 0.511), (0.000, 0.000, 0.656)
C28	55	7.298	7.728	2.535	(0.398, 0.039, 0.0), (0.376, 0.151, 0.5) (0.207, 0.270, 0.5), (0.239, 0.384, 0.0) (0.015, 0.196, 0.5), (0.460, 0.408, 0.0)
4H-diamond	195	2.534	-	8.355	(0.000, 0.000, 0.093), (0.667, 0.333, 0.155)

Table 7. Lattice parameters for carbon allotropes calculated with Pople’s 6-21 basis set and B3LYP exchange-correlation functional

Structure	N	a, Å	b, Å	c, Å	Atomic positions
diamond	227	3.594	-	-	(0.125, 0.125, 0.125)
lonsdaleite	194	2.527	-	4.205	(0.333, 0.667, 0.063)
mtn	227	9.688	-	-	(0.880, 0.068, 0.683), (0.125, 0.125, 0.625) (0.033, 0.033, 0.716)
SiC12	166	2.534	-	25.067	(0.333, 0.667, 0.073), (0.333, 0.667, 0.916) (0.333, 0.667, 0.844), (0.667, 0.333, 0.999)
C28	55	7.301	7.735	2.538	(0.398, 0.039, 0.0), (0.375, 0.151, 0.5) (0.268, 0.270, 0.5), (0.239, 0.384, 0.0) (0.015, 0.197, 0.5), (0.460, 0.408, 0.0)
4H-diamond	195	2.513	-	8.266	(0.000, 0.000, 0.093), (0.667, 0.333, 0.156)

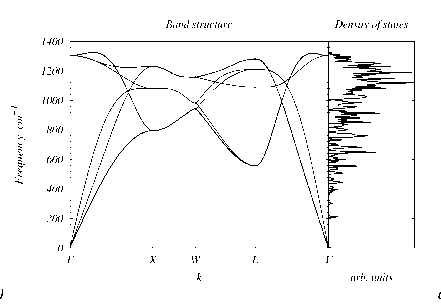
arb. units

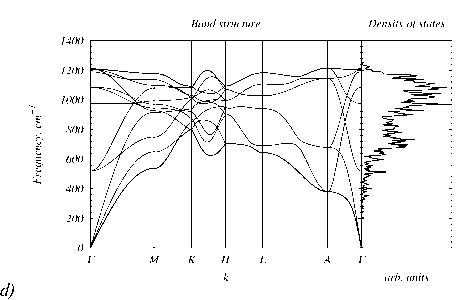
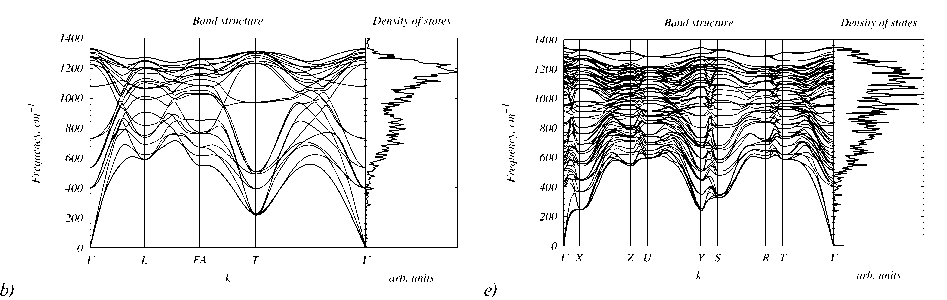
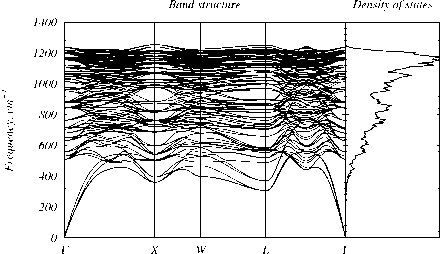
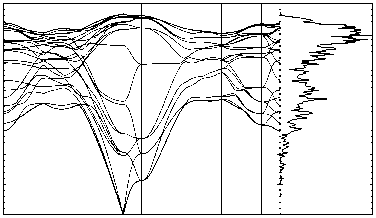
Fig. 4. Phonon band structures and density of states of allotropes: a) diamond, b) SiC12, c) mtn, d) lonsdaleite, e) C28, f) 4H-diamond

Band structure

Density of states

К

H

L M arb. units

M

c)

f)