Оптическая диагностика дефектов в слоистых периодических наноструктурах

DOI:

Актуальность изучения фотонных кристаллов обусловлена тем, что данная сфера современного материаловедения широко развивается в мире науки, так как уникальность фотонных кристаллов заключается в их структуре, свойства которой имеют периодическое изменение показателя преломления. Общее описание свойств фотонных кристаллов можно найти в [1; 4; 6; 11]. Основы теории оптики слоистых структур описаны в фундаментальной работе [2]. Это динамично развивающаяся область современного материаловедения. Полное исследование характеристик частиц a-SiO2 в синтетических опалах описано в [8]. Структура и оптические свойства слоистых нанокомпозитов ZnSe / SiO2, полученных методом радиочастотного магнетронного распыления, были изучены в [7]. В [3] изучались свойства новых материалов, созданных в результате наполнения искусственных опалов различными сегнетоэлектриками, такими как нитрит натрия, титанат бария, ниобат лития и др.

Структура фотонных кристаллов является их особой, отличной от других материалов, спецификой. Периодическое изменение показателя преломления является главной особенностью свойств структуры фотонных кристаллов.

Дисперсия таких кристаллов всех типов возможна при одинаковом порядке параметра решетки кристалла и длины волны излучения. Поскольку фотонные кристаллы прозрачны для основного спектра электрического излучения, они не пропускают свет с длиной волны, сравнимой со временем фотонно-кристаллической структуры.

Поскольку производство таких кристаллов является трудоемким и дорогостоящим, важен предварительный анализ гипотетических структур. Например, в [5] представлена программа, решающая задачу – распространение света через слоистую среду. В [12] при участии одного из авторов было рассмотрено распространение акустических волн через слоистую структуру, а в [10] был предложен анализ лазерной термометрии, основанный на отражении и пропускании лазерного излучения диэлектрическим слоем.

Рассмотрим падение плоской гармонической световой волны из вакуума на слоистую периодическую среду, занимающую область от z = 0 до z = d. Область z > d представляет собой подложку, заполненную однородным диэлектриком. Слоистая среда состоит из периодически повторяющихся слоев с заданными диэлектрическими постоянными (рис. 1). Требуется раз-

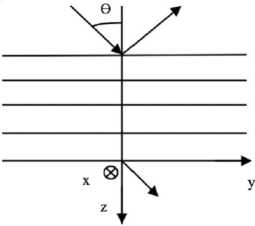
Рис. 1. Геометрия отражения волн от слоистой среды.

Толщина слоя: 1 = 100 Нм; 2 = 160 Нм; 3 = 80 Нм; 4 = 120 Нм. Угол падения 0 = 45°

работать алгоритм и реализовать программный комплекс для расчета коэффициентов отражения и пропускания амплитуды и энергии для такой слоистой периодической среды. Разработанный программный продукт применяется для анализа спектров отражения и пропускания слоистых периодических наноструктур.

Обозначим через A, R и T амплитуды электрических векторов падающей, отраженной и преломленной волн, а ε1, μ1 и ε2, μ2 – диэлектрическая и магнитная проницаемости граничных сред, а θ1 и θ2 – углы между нормалями к падающей и проходящей волнам и направлениями оси z.

Эти параметры связаны матричным уравнением:

Рассмотрим случай однородной диэлектрической пленки, расположенной между двумя однородными средами. Все носители будут считаться немагнитными (µ = 1).

Характеристическая матрица однородной диэлектрической пленки имеет вид:

M(z) =

cos(k0nzcos9) - ^sin(k0nzcos9)

—ipsin(k0nzcos9) cos(k0nzcos9)

/ cost)

M =       '

\-ip2sinp

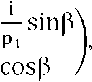
где

Q 2л

P = Гп2            (7a)

и

(Л + Д \ _ /т^ ^i2\ / Т \       ГП p^A-R)) vn21 тп22)\р1Т).       (1)

Для коэффициентов амплитудного отражения и пропускания получены следующие окончательные результаты:

R (m₁₁+m₁₂pOPi-(.m₂₁+m₂₂pO ^. (2)

A (m11+m12pl)p1+(m21+m22pl) v 7

Т                2Р1

. (3)

A (m11+m12pl)p1+(m21+m22pl) v 7

Коэффициент отражения и пропускания, выраженный через r и t, имеют вид:

Pl IT 12

RR = |Л|² ,        TT =^^|т| .         (4)

Фазу δR от R можно назвать изменением фазы во время отражения, а фазу δT от T можно назвать изменением фазы во время передачи. Изменение фазы δR относится к первому интерфейсу, в то время как δT относится к плоской границе раздела между слоистой средой и подложкой.

Соответствующие формулы для волны p-поляризации немедленно получаются из (2)– (4) путем замены величин p1 и pl величинами:

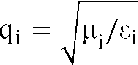
В этом случае R и T являются отношением амплитуд магнитных, а не электрических векторов.

pj = njcosθj, j = 1,2,3. (7b)

В случае, когда вместо однородной пленки мы берем слоистую структуру с характерными матрицами слоев М1, М2, ... Mn, полученную матрицу можно рассчитать как:

M(zN) = M1(z1)M2(z2–z1)* ... *MN(zN–zN–1). (8)

Причина возможного нахождения матрицы путем умножения заключается в том, что на границе каждого слоя выполняется условие непрерывности векторов столбцов Q на границе каждого слоя.

Qlzr=QIZ1+. (9)

Этот вывод следует из непрерывности составляющих векторов поля Еx и Нy, образующих вектор столбца Q.

Из анализа следует, что необходимо создать программный алгоритм, позволяющий нам умножать матрицы отдельных слоев для любого фиксированного количества этих слоев. То же самое относится и к случаю, когда некоторые слои объединяются в отдельную структуру и затем периодически повторяются.

сложение и умножение комплексных чисел, умножение комплексного числа на рациональное число, нахождение сопряженного и модуля. Для построения графических объектов используется графическая библиотека Xlib.h. В данном случае рассматривать тип данных конкретной переменной не является первостепенной задачей. Основная часть программы состоит из одной функции, которая называется main.

Основную часть функции можно представить в следующем виде:

• 1.    Создание первичных данных.

• 2.    Расчет необходимых параметров и построение матрицы характеристик для определенного угла падения.

• 3.    Сохранение коэффициентов отражения и пропускания в выходном файле.

• 4.    Построение графического изображения поведения коэффициентов отражения и пропускания для первоначальной оценки построенной модели.

• 10.    int main()

• 11.    {double A=0.1, n[N]={1,3.09,2.38,1.87,3.42,1}, p[N],be[N-1],te[N], l0[100],h[N-1] ={0,100, 160,80,120},RR[100],TT[100],hw[100];

• 12.    Complex Mr[2][2], T[100], R[100], M[N-1] [2][2],r,t;

• 13.    int m;

• 14.    hw[0]=0.09;

• 15.    for(m=1;m<100;m++)

• 16.    hw[m]=hw[m-1]+0.09;

• 17.    for(m=1;m<100;m++)

• 18.    l0[m]=299792458*4.135667662(hw[m] *1000000);

• 19.    te[0]=3.1416/6;

• 20.    for(int i=1; i

• 21.    te[i]=asin(sin(te[0])*n[0]/n[i]);

• 22.    for(int i=0; i

• 23.    p[i]=cos(te[i])*n[i];

• 24.    for(m=0;m<100;m++)

• 25.    {for(int i=1; i

• 26.    { be[i]=6.2832*n[i]*h[i]*cos(te[i])/l0[m];}

• 27.    Complex k(2*p[0],0);

• 28.    for(int i=1; i

• 29.    { M[i][0][0].Re=cos(be[i]);

• 30.    M[i][0][1].Im=(-1)*sin(be[i])/p[i];

• 31.    M[i][1][1].Re=cos(be[i]);

• 32.    M[i][1][0].Im=(-1)*sin(be[i])*p[i]}

• 33.    Mr[0][0]=M[1][0][0];

• 34.    Mr[0][1]=M[1][0][1];

• 35.    Mr[1][0]=M[1][1][0];

• 36.    Mr[1][1]=M[1][1][1];

• 37.    for (int i=2; i

• 38.    {Complex Temp[2][2];

• 39.    Temp[0][0]=Mr[0][0]*M[i][0][0] +Mr[0][1]*M[i][1][0];

• 40.    Temp[0][1]=Mr[0][0]*M[i][0][1]+ Mr[0][1]*M[i][1][1];

• 41.    Temp[1][0]=Mr[1][0]*M[i][0][0]+ Mr[1][1]*M[i][1][0];

• 42.    Temp[1][1]=Mr[1][0]*M[i][0][1]+ Mr[1][1]*M[i][1][1];

• 43.    Mr[0][0]=Temp[0][0];

• 44.    Mr[0][1]=Temp[0][1];

• 45.    Mr[1][0]=Temp[1][0];

• 46.    Mr[1][1]=Temp[1][1];}

• 47.    r = ((Mr[0][0]+Mr[0][1]*p[N-1])*p[0]-(Mr[1][0]+Mr[1][1]*p[N-1]))/ ((Mr[0][0]+Mr[0][1]*p[N-1]) *p[0]+(Mr[1][0]+Mr[1][1]*p[N-1]));

• 48.    t=k/((Mr[0][0]+Mr[0][1]*p[N-1]) *p[0]+(Mr[1][0]+Mr[1][1]*p[N-1]));

• 49.    RR[m]=r.Mod()*r.Mod();

• 50.    TT[m]=p[N-1]*t.Mod()*t.Mod()/p[0];

• 51.    R[m]=r*A;

• 52.    T[m]=t*A; }

• 53.    ofstream foutRR(“RR.txt”), foutTT(“TT.txt”), foutRre(“Rre.txt”), foutTre(“Tre.txt”), foutRim(“Rim.txt”),foutTim(“Tim.txt”);

• 54.    for(int i=0; i<100;i++)

• 55.    { foutRR<

• 56.    foutTT<

• 57.    foutRre<

• 58.    foutTre<

• 59.    foutRim<

• 60.    foutTim<

• 61.    foutRR.close();

• 62.    foutTT.close();

• 63.    foutRre. close();

• 64.    foutTre.close();

• 65.    foutRim.close();

• 66.    foutTim.close();

• 67.    txCreateWindow (maxX,maxY);

• 68.    txLine (30,30,30,maxY-30);

• 69.    txLine (30,maxY-30,maxX-30,maxY-30);

• 70.    float mX,mY;

• 71.    mX=(maxX-60)/90;

• 72.    mY=(maxY-60);

• 73.    for(int i=1;i<10;i++)

• 74.    txLine (i*10*mX+30,maxY-35,i*10*mX+ 30,maxY-25);

• 75.    txTextOut (10*mX+20,maxY-20, “10”);

• 76.    for(int i=1;i<11;i++)

• 77.    txLine (25,maxY-(0.1*i*mY+30),35,maxY-(0.1*i*mY+30));

• 78.    txTextOut (40,maxY-(0.1*mY+40), “0.1”);

• 79.    for (int i=0;i<99;i++)

• 80.    { txSetColor (TX_YELLOW);

• 81.    txLine (i*mX+30,maxY-(RR[i]*mY+30), (i+1)*mX+30,maxY-(RR[i+1] *mY+30));

• 82.    txSetColor (TX_GREEN);

• 83.    txLine (i*mX+30,maxY-(TT[i]*mY+30), (i+1)*mX+30,maxY-(TT[i+1] *mY+30));}

• 84.    return 0;}

Ниже приведен подробный алгоритм работы программы.

Входными данными программы являются: количество слоев N; толщина слоя h [N-1]; показатель преломления n [N], длина волны падения l0 (строка 11).

Расчет угла между нормалями к падающей и проходящей волнам te [N] (строки 20–21), а также be [N-1] (строка 26) в соответствии с формулой (7a) и p [N] (строка 23) в соответствии с формулой (7b). Кроме того, M [N-1] [2] [2]] (строки 28–32) – матрица характеристик для каждого слоя рассчитывается по формуле (5). Результирующая матрица Mr [2] [2] (строки 33–46) – является результатом произведения характеристических матриц по формуле (8). В соответствии с формулами (2), (3), (4), рассчитаны коэффициенты отражения R [91] и пропускания T [91] (строки 47–52).

Данные, сохраненные в выходных файлах (строки 53–66): “Rre.txt “ является реальной частью изменения фазы при размышлении; “Rim.txt “ является мнимой частью изменения фазы при отражении; “Tre.txt “ – реальная часть изменения фазы при прохождении; “Tim.txt “ – мнимая часть изменения фазы во время передачи; “RR.txt “ – коэффициент отражения; “TT.txt “ – коэффициент пропускания.

Используя графическую библиотеку, изображение поведения коэффициентов отра- жения и пропускания строится в виде кусочнолинейного графика (строки 61–83).

На рисунке 2 показан частотный спектр коэффициентов отражения и пропускания при прохождении через слоистую периодическую структуру (Cu2O/Si/Ag2O/C) при разных углах падения α. Толщина слоя: 100 Нм, 160 Нм, 80 Нм, 120 Нм. Длина волны падающего излучения составляет 640 Нм. Количество повторений структуры: 10. Входные данные программы: n[n]={1,3.24,3.42,2.97,2.38 ,1}, l0=640h[N-1]= {0,100,160,80,120}, C = 10.

На рисунке 3 показан частотный спектр коэффициентов отражения и пропускания при прохождении через слоистую периодическую

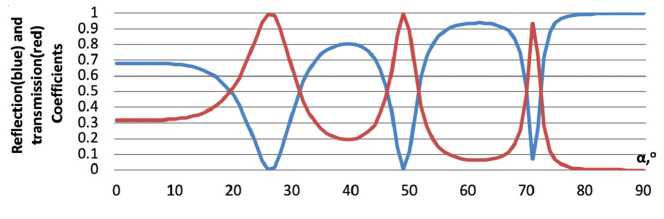
Рис. 2. Коэффициенты отражения энергии (синий) и пропускания (красный) при различных углах падения α при прохождении через слоистую структуру Cu2O/Si/Ag2O/C

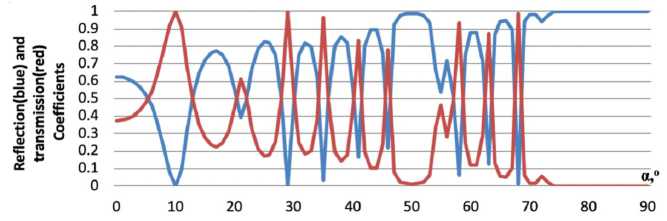
Рис. 3. Коэффициенты отражения энергии (синий) и пропускания (красный) при различных углах падения α при прохождении через слоистую структуру Cu2O/Si/Ag2O/C с дефектным слоем

структуру (Cu2O/Si/Ag2O/C) при разных углах падения α. Толщина слоя: 100 Нм, 160 Нм, 80 Нм, 120 Нм. Длина волны падающего излучения составляет 640 Нм. Количество повторений структуры: 10. Дефект: толщина второго слоя в пятом периоде составляет 800 Нм. Входные данные программы: n[n]={1,3.24,3.42, 2.97,2.38 ,1}, l0=640h[N-1]= {0,100,160,80,120}, C=10 ,o=5, q=2, d=5.

Вопрос анализа дефектов в периодических структурах важен, так как нарушение периодичности в них может привести к рассеянию энергии электромагнитного поля на дефектах. Для описания последнего была создана программа, получившая официальную регистрацию в реестре компьютерных программ [9]. Например, были рассчитаны энергетические коэффициенты отражения и пропускания для слоистой периодической структуры с дефектом и без него из следующих компонентов: слой оксида меди Cu2O толщиной 100 Нм, слой кремния Si толщиной 160 нм, слой оксида серебра Ag2O толщиной 80 Нм, слой алмаза толщиной 120 Нм. Программа используется для анализа частотного спектра волны, проходящей через исследуемую слоистую периодическую структуру.

На основе этого можно сделать вывод, что спектральная зависимость этих коэффициентов имеет ярко выраженную интерференционную картину. Из этого рисунка можно извлечь информацию о структуре слоистой периодической среды.

Результаты, полученные с помощью разработанной компьютерной программы, могут быть использованы для спектрального анализа при исследовании слоистых периодических сред с различными конфигурациями структуры и наличием дефектов, а также при анализе дефектов в одномерных фотонных кристаллах.