Оптическая сила, действующая на частицу, в присутствии обратного потока вблизи фокуса градиентной линзы

Изучение силы, действующей со стороны света на нанообъекты, до сих пор является актуальной темой исследований [1–11]. В последние годы особенный интерес вызывают исследования, где рассматривается действие силы на объекты размером порядка сотен нанометров. Это связано с тем, что диэлектрические и металлические частицы с таким характерным размером являются наиболее перспективными как детали для создания метаповерхностей [12– 16]. Расчет силы действия света на такие частицы производится, как правило, в дипольном приближении [17, 18], что ограничивает применимость таких результатов. Например, в [19] численно и экспериментально была изучена подвижность похожих на стержни частиц, которая появлялась из-за действующего со стороны света момента силы. Расчеты проводились в дипольном приближении. А в [20] авторы аналитически изучали момент силы, действующий на пару наношаров. Момент силы так же был рассчитан в дипольном приближении. Авторы в [21] рассмотрели силу, действующую со стороны некоторых Бесселевых пучков на наночастицы, которая рассчитывалась с помощью тензора напряженностей Максвелла, и обнаружили, что данная сила может быть отрицательной (обрат- ной) и может быть направлена к источнику света, несмотря на отсутствие градиентной составляющей силы при постоянной интенсивности вдоль оптической оси. Сами же поля рассчитывались с помощью обобщенной теории Лоренца-Ми. При этом авторы утверждают, что наличие обратного потока интенсивности [22–24] (отрицательной проекции вектора Пойнтинга на ось распространения света) не является ни необходимым, ни достаточным условием для возникновения обратной силы. Свои расчеты они приводили для полистироловых частиц диаметром от 0 до 4 мкм при длине волны света λ = 1,064 мкм. А в [25] авторы на основании эффекта «оптического трактора» экспериментально доказали возможность захвата, группировки и сортировки наночастиц размером 600–800 нм при длине волны света 532 нм. Расчет действия силы производился в дипольном приближении.

Из приведенного краткого обзора можно сделать вывод, что строгий метод расчета силы на основании тензора напряжений Максвелла используется редко из-за большого объема вычислений. Кроме того, обратную силу искали для сравнительно больших (сотни нанометров – единицы микрометров) шариков, в то время как для шариков диаметром в десятки и сотни нанометров эффект обратной силы подробно не рассматривался.

В этой работе рассмотрена обратная сила, дей- ствующая на наношары с диаметром от 70 до 350 нм. Показано, что на наношары, состоящие как из оптически прозрачного материала (n = 1,5 – стекло), так и из поглощающих материалов (n = 1,5 + 0,3i, а также золото) при расположении в остром фокусе высокоапертурной градиентной микролинзы действует обратная сила (то есть продольная проекция вектора силы отрицательная). При этом рассмотрены случаи наличия и отсутствия обратного потока интенсивности и показано, что, хотя обратная сила возникает независимо от его наличия, обратный поток оказывает влияние на величину силы – увеличивает её по модулю. Кроме того, показано, что вырез в выходной плоскости градиентной линзы существенно увеличивает действующую на наношар силу, позволяя его затягивать внутрь выреза, где интенсивность света и его действие на наношар максимальны. Такую градиентную линзу можно использовать в качестве «оптического магнита» для наночастиц. Расчеты светового поля производились с помощью FDTD-метода в пакете FullWAVE с высокой подробностью, в области расположения наношаров использовался шаг сетки отсчетов λ / 400, а расчет силы со стороны света про-

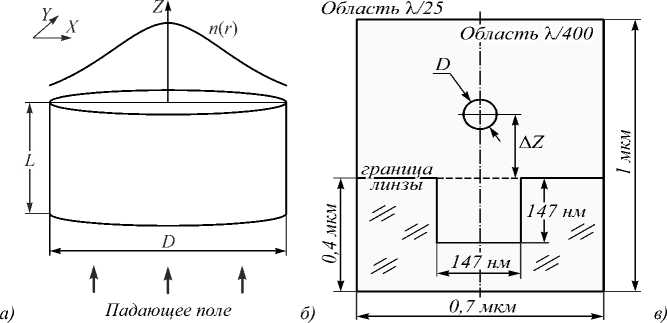
фаза падающего поля, имеющего левую круговую поляризацию и вихрь m = 2 (в)

Падающее поле было ограничено апертурой, равной диаметру линзы. На выходной поверхности линзы было сделано цилиндрическое отверстие диаметром 147 нм и глубиной внутрь линзы 147 нм. В [26] было показано, что такого размера отверстие максимизирует (по модулю) обратный поток энергии S z = (1/2)Re [ E *x H ] z на выходной поверхности линзы (50 нм за ней). На оптической оси располагался наношар диаметром D =70 нм.

Моделирование методом FDTD проводилось для трёх случаев: когда показатель преломления шара был равен n = 1,5 (стекло), n = 1,5 + 0,3i (стекло с поглощением), n =0,52+ 10,7i (золото). Для расчета распространения света методом FDTD использовалась переменная сетка отсчетов. Разбиение по всей линзе и за её пределами составляло λ /25 по всем трем осям координат. Интересующая область вокруг щели в изводился строгим методом на основании тензора напряженности Максвелла.

Постановка задачи

Расчеты производились в фокусе градиентной линзы Микаэляна, рассчитанной для фокусировки излучения на своем торце [26]. Показатель преломления такой линзы изменяется в соответствии с формулой:

- 1

,                                    (1)

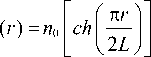
где n 0 = 3,47 – показатель преломления линзы на оси, r – радиальная координата, L – длина линзы. Диаметр линзы был равен D = 11,7 мкм, длина линзы L = 5,877 мкм, длина волны падающего света λ = 1,55 мкм. Показатель преломления на оси линзы n (0) = 3,47 (кремний), на краю линзы n ( D /2)= 1,0. На одну из поверхностей такой линзы нормально падал плоский пучок света, имеющий левую круговую поляризацию и фазовый вихрь порядка m =2 (рис. 1). Известно [26], что в таком случае образуется обратный поток энергии и интенсивность, близкая к максимальной на оптической оси.

Рис. 1. Рассматриваемая градиентная линза (а) и схема (её сечение в плоскости XZ) расположения шара в щели (б),

границах X, Y e (-0,35 мкм; 0,35 мкм), Z e (5,48 мкм; 6,48 мкм) моделировалась с повышенной точностью (рис. 1 б ), шаг сетки в этой области по всем трем осям составлял λ / 400. При увеличении разбиения в интересующей области до λ /600 полученные значения силы изменялись менее чем на 7,2% в точке на графике с максимальным различием, однако время моделирования возрастало примерно в полтора раза, поэтому выбор был сделан в пользу разбиения λ / 400. Расчет сил производился по полю вокруг шара по формуле:

F = -<^(g-n)dS, (2) S где n - внешний вектор нормали к поверхности S, а -тензор напряжений электромагнитного поля Максвелла, компоненты которого в системе СГС имеют вид :

)

- E i E k - H i H k

где E i , H i – компоненты электрического и магнитного полей, 5 ik - символ Кронекера ( 5 i = k = 1, 5 i * k = 0).

Падающее поле – левая круговая поляризация и фазовый вихрь m = 2

На рис. 2 представлены результаты моделирования силы и момента силы, действующей на наношар при описанных выше условиях.

Из рис. 2а видно, что, если золотая частица расположена в начале выреза, на нее действует положительная сила вдоль оптической оси. Но по мере сме- щения в положительном направлении вдоль оси Z она доходит до точки устойчивого равновесия примерно на расстоянии от границы линзы A Z=-45 нм. В случае частицы с показателем преломления n=1,5 без поглощения и с поглощением n = 1,5 + 0,3i проекция силы Fz на том же интервале остается отрицательной, однако по модулю они меньше приблизительно в 3,5 раза, чем для наношара из золота. На рис. 2б приведен момент силы, вращающий наношар из тех же материалов вокруг оптической оси Z и рассчитанный относительно центра шара. Расчет момента силы производился по формуле [27]:

M = ^r х ( о- n ) ] dS , (4) S

Fz, nH (падающая .мощность 0,1 Вт)    Sz, отн.ед.

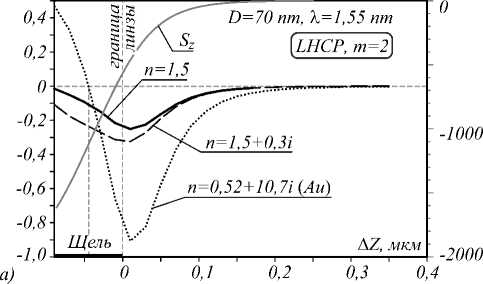
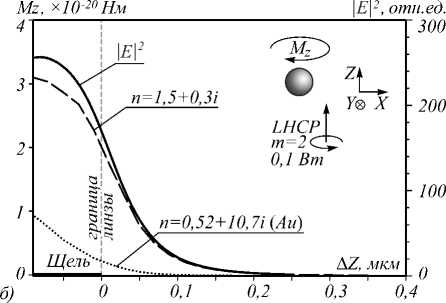
Рис. 2. Зависимость проекции силы Fz (а) и момента M z = [ r ^ F ] z (б), действующих на шар, от координаты шара A Z относительно границы линзы, и интенсивность света |E|² на оптической оси.

Падающая волна – левая круговая поляризация с фазовым вихрем m = 2

где r – радиус-вектор от точки, относительно которой рассчитывается момент силы, до точки интегрирования на поверхности S . Можно заметить, что момент, действующий на шар из золота, примерно в 3 раза меньше момента, действующего на поглощающую частицу, что связано с бόльшим отражением от золота и меньшей передачей момента наношару со стороны света. Момент силы, действующий на непоглощающую частицу с n = 1,5, равен нулю. Разность в направлении вращения вектора падающего на линзу электрического поля и момента M z обусловлена тем, что после фокусировки света направление вращения электрического вектора меняется на противоположное. В фокусе линзы и направление вращения вектора электрического поля, и направление действия момента M z совпадают по направлению. Из рис. 2 а видно, что в присутствии обратного потока энергии отрицательная сила, действующая на диэлектрическую поглощающую частицу, больше, чем действующая на непоглощающую.

Круговая поляризация без фазового вихря

На рис. 3 показаны зависимости проекции силы Fz от расположения шара для рассматриваемых показателей преломления, но падающее на линзу поле имеет левую круговую поляризацию при плоском волновом фронте с постоянной фазой. При таком начальном поле в фокусе линзы обратный поток интенсивности не образуется.

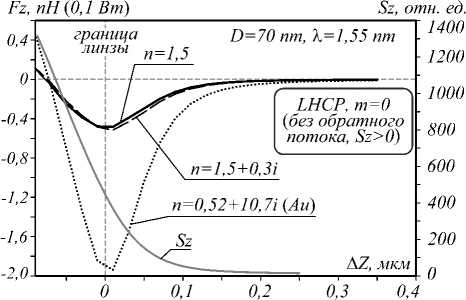
Рис. 3. Зависимость проекции силы Fz (а), действующей на шар, от координаты шара A Z относительно границы линзы. Падающая волна с левой круговой поляризацией

Видно, что при отсутствии фазового вихря проекция силы Fz, действующая на шар из золота на границе линзы, по модулю выросла в 2,1 раза, в то время как на поглощающий шар она выросла всего на 52%, а на непоглощающий – на 97%. При этом для шара из золота в начале графика (координата шара ΔZ =–90 нм) проекция силы Fz = 0,45 пН для обоих падающих полей, несмотря на разницу в интенсивности на оптической оси, приведенную на рис. 4.

|£р. отн.ед.

б)       -0,2 -0,1     0     0,1    0.2

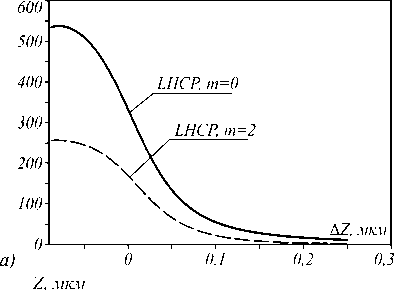
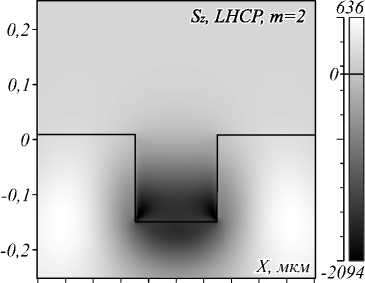
Рис. 4. Интенсивность |E|2 на оптической оси для случая круговой поляризации с фазовым вихрем m = 2 и наличием обратного потока интенсивности и в отсутствие фазового вихря m = 2 (а) и проекция вектора Пойнтинга Sz на ось Z в случае падающего поля с левой круговой поляризацией и фазовым вихрем m = 2 в плоскости XZ (б)

Из рис. 2–4 видно, что для непоглощающей частицы, равно как и для частицы из золота, график силы не пропорционален интенсивности света, которая в фокусе на оптической оси для двух начальных падающих полей близка по форме, но различается в 1,99...2,09 раз в рассматриваемом диапазоне значений Δ Z . В случае в два раза меньшей интенсивности света на оптической оси было бы логично ожидать уменьшения силы, действующей на все три наношара, так же в два раза. Но мы наблюдаем, что в случае наличия обратного потока вектора Пойнтинга (рис. 4 б ) сила, действующая на поглощающий шар и шар из золота, по модулю больше ожидаемого и направлена назад, в сторону источника света, что доказывает влияние обратного потока.

Влияние на проекцию силы размера частицы

Интересной выглядит зависимость продольной проекции силы, действующей на шар, от его размера. На рис. 5 приведены зависимости проекции силы Fz от размера наношара, расположенного за линзой. Для того, чтобы корректно рассчитать силу, расстояние от границы линзы (без щели) до центра частицы было выбрано 0,25 мкм. Расчёты проводились с диаметром наношара D от 0,07 до 0,35 мкм.

Из рис. 5 видно, что при росте до диаметра D =0,2 мкм сила на наношары со всеми тремя показателями преломления растет по модулю и остается отрицательной, но затем с дальнейшим ростом диаметра золотая частица начинает выталкиваться из пучка, в то время как поглощающая и диэлектрическая частицы продолжают испытывать отрицательную силу. Причем поглощающая частица притягивается назад к линзе немного сильнее, чем диэлектрическая без поглощения.

F=, пН(0,1Вт)

LHCP, т=0

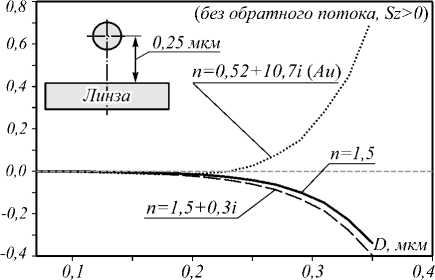
Рис. 5. Зависимость проекции силы Fz, действующей на шар, от диаметра шара D. Расстояние от центра шара до границы линзы было взято 0,25 мкм

Заключение

В работе рассчитана продольная проекция силы Fz , действующая на наношар в остром фокусе градиентной гиперболической секансной линзы с вырезом на оптической оси. Показано, что для малых частиц, близких по размеру к критерию Рэлея, имеет место обратная сила, которая тянет частицу назад, в сторону к источнику света. Показано, что в двух схожих распределениях интенсивности на оптической оси в фокусе линзы при наличии и отсутствии обратного потока проекция силы на оптическую ось Fz отрицательна и по отношению к интенсивности больше в том случае, когда обратный поток присутствует. Этот эффект больше выражен для поглощающих частиц и для частиц из золота. Показано также, что для частицы из золота характерна обратная сила при малом размере частицы (шар диаметром 70 нм при длине волны света λ = 1,55 мкм). Эта сила достигает величины Fz =– 1,9 пН при расположении наношара на границе линзы при падающем поле – левой круговой поляризации без фазового вихря, и превышает в 3,9 раз по модулю проекции силы Fz в случае непоглощающего ( n = 1,5) или поглощающего ( n = 1,5 + 0,3 i ) наношара. При этом мощность падающего пучка во всех случаях одинакова и равна 100 мВт. Обратная сила для наношара из золота пропадает при увеличении его диаметра, что согласуется с выводами в работе [21].

Работа выполнена при поддержке Российского научного фонда в частях «Падающее поле – левая круговая поляризация и фазовый вихрь m =2» и «Круговая поляризация без фазового вихря» (грант 18-1900595), Российского фонда фундаментальных исследований (грант 18-29-20003, 18-07-01380) в частях «Постановка задачи», «Влияние на проекцию силы размера частицы» а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в частях «Введение» и «Заключение».