Оптические чистые вихри и гипергеометрические моды

Давно известны и нашли широкое применение в оптике моды Эрмита-Гаусса (ЭГ) и Лагерра-Гаусса (ЛГ), которые являются частными решениями параксиального волнового уравнения (ПВУ) (или уравнения Шредингера) в декартовых и цилиндрических координатах [1]. Они являются поперечными модами стабильных лазерных резонаторов. Эти моды сохраняют свою структуру (распределение интенсивности и фазы в поперечном сечении), изменяясь при распространении вдоль оптической оси только масштабно. Эти моды также образуют ортогональный базис, так что с помощью линейной комбинации этих мод можно строить другие решения ПВУ.

В цилиндрических координатах ПВУ имеет и другие модовые решения, которые также, как и моды ЭГ и ЛГ, сохраняют свою структуру, меняясь только масштабно. Это параксиальные моды Бесселя [2], которые надо отличать от непараксиальных бездифракционных пучков Бесселя, которые являются решениями уравнения Гельмгольца [3] и здесь не рассматриваются. В отличие от гауссовых мод моды Бесселя имеют бесконечную энергию (хотя конечную интенсивность в каждой точке пространства) и расходятся линейно. То есть эффективный диаметр пучка Бесселя линейно возрастает с увеличением расстояния вдоль оптической оси от начальной плоскости. Известно, что гауссовые моды расходятся параболически, и только при большом удалении от начальной плоскости радиус гауссового пучка растет тоже линейно с ростом расстояния вдоль оптической оси.

В последнее время были введены в рассмотрение новые модовые решения ПВУ [4-8], которые изучались теоретически [4-7] и экспериментально [8]. Это световые пучки Айнса-Гаусса. Они являются решениями ПВУ в эллиптических координатах. В этих координатах ПВУ решается методом разделения переменных, и решение получается в виде произведения гауссовой функции на многочлены Айнса. Сами же многочлены Айнса являются решениями уравнения Уиттекера-Хилла [2]. Моды Айнса-Гаусса (АГ) являются ортогональным базисом, обобщающим моды ЭГ и ЛГ. Когда эллиптические координаты переходят в цилиндрические (эллипсы переходят в окружности), то моды АГ переходят в моды ЛГ, а при стремлении эксцентриситета эллипсов к беско- нечности (эллипсы переходят в отрезок прямой) моды АГ переходят в моды ЭГ.

Заметим, что в [9] исследовались астигматические лазерные пучки, названные модами Эрмита-Лагерра-Гаусса, которые также при определенном значении параметра (угла поворота цилиндрической линзы вокруг оптической оси) переходят в обычные моды ЭГ и ЛГ.

В данной работе рассмотрен еще один тип модовых решений ПВУ в цилиндрических координатах, которые также сохраняют свою структуру, изменяясь только масштабно. Расходимость этих мод гиперболическая, то есть при большом удалении от начальной плоскости эти пучки расходятся слабее, чем гауссовые и бесселевые пучки. Так как функции, описывающие эти моды, содержат вырожденную гипергеометрическую функцию, то мы назвали их гипергеометрическими (ГГ) модами. Они как и параксиальные моды Бесселя обладают бесконечной энергией. На практике их можно сформировать только на конечном расстоянии с помощью спиральной фазовой пластины [10-12], освещенной плоской волной. Так как у любой ГГ моды всегда (кроме начальной плоскости) в центре (на оптической оси) имеется нуль интенсивности, характерный для оптических вихрей [13], и ни освещающий пучок, ни сама спиральная пластинка не вносят дополнительной расходимости в пучок, то эти моды можно считать «чистыми» вихрями.

В работе установлено, что найденные решения являются однопараметрическим семейством более общего двухпараметрического класса решений ПВУ в цилиндрических координатах [2]. Впервые о гипергеометрических модах, по видимому, упоминалось в [10,14].

2. Чистые вихри – параксиальные световые пучки с минимальной расходимостью

ПВУ в цилиндрических координатах имеет вид:

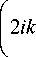
d d² 1 _d_ d z 8 r ² r 8 r

1 82 )

- ^1 E ( r , 0 , z ) = 0, r ОУ )

где (r, θ ) - поперечные полярные координаты, z - координата, направленная вдоль оптической оси, k -волновое число. Если искать радиально-симметричное решение уравнения (1) в виде неполного разделения переменных

л

E ( r , 6 , z ) = E

E 2 ( 6 ) E з ( z ),      (2)

то получатся моды ЛГ [1], которые не изменяют свою интенсивность E ( r , 6 , z )| 2 в системе координат

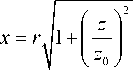
cos 6 ,

1 I------------                                             (3)

y = Г а ¹ + 1 ^— I Sin 6 ,

)

_ z = z, где z„ = 0 , r0 -радиус гауссового пучка при z=0, 02

k =2π/λ, λ – длина волны излучения.

Менее известно другое решение уравнения (1), которое также является решением с неполным разделением переменных, и не меняет своей интенсивности в системе координат [2]:

x = rz cos 6, y = rz sin 6,                                      (4)

z = z .

Из уравнения (9) видно, что световое поле (5) может быть сформировано с помощью узкой кольцевой щели радиуса γ в непрозрачном экране, а плотность световой энергии в щели должна быть бесконечно большой.

Из уравнений (5) и (6) следует, что при z , стремящемся к нулю, вблизи экрана радиус бесселевого пучка r_0m также стремится к нулю.

Теперь найдем еще одно решение уравнения (1) с неполностью разделенными переменными, расходимость которого при больших z будет «слабее», чем расходимость мод ЛГ (8) и параксиальных мод Бесселя (6). Будем искать решение в виде:

( kr ² 1

E ( r , 6 , z ) = E n I — | exp( in 6 ), I 4 z )

kr ²

где n - целое число. Для функции E „( t ) где t =----,

4z вместо уравнения (1) получим уравнение:

d ² dn ²

t —77 + (1 — 2 it)--- dt2           dt   4t

E n ( t ) = 0.

Будем искать решение уравнения (11) в виде:

E n ( t ) = tete ^u V n ( t ),                                    (12)

тогда для функции Ψ n ( t ) получим уравнение:

Линейно-независимыми решениями уравнения (1)

такого типа являются параксиальные моды Бесселя:

V m _T ( r , 6 , z ) =

/V (—1)mk T ( kYr 1, J        X m I I V2n z | z )

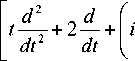
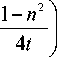
V n ( t ) = 0.

_ . ik ( 2 , 2 \ ■ a exp —( r + y ) + im 6 .

2 z^x '

Пусть частное решение уравнения (13) имеет вид

V n ( t ) = iJ _v ( t ) + J _{v+ 1}( t ),

где m – целое число, γ > 0 – модовый параметр (радиус узкой щели), характеризующий масштаб моды Бесселя. Из уравнения (5) видно, что параксиальный пучок Бесселя расходится линейно с увеличением

тогда, подставив выражение (14) в уравнение (13), получим, что ν= ( n– 1)/2, n – целое число. Окончательно находим счетное число линейно-независимых решений уравнения (1):

расстояния z :

X z « m r0 m     ~     ,

2 яу

где r 0m – радиус первого нулевого кольца моды Бесселя m- го порядка, α_m – первый ненулевой корень функции Бесселя, J_m(α_m)= 0 .

Линейная расходимость характерна также для мод ЛГ в дальней зоне. Так как радиус основной моды ЛГ з ависит о т z известным образом:

I I

1 + I- | ,                                   (7)

I ^z 0 )

то при z >> z 0 получим:

X z r ®---- .

Л ^r 0

При z, стремящемся к нулю, функция (5) стремится к функции

V m Y ( r , 6 , z ^ 0) = ^^{( r Y} ) exp( im 6 ). J 2 n r

_ , „ _x П Г . n ( n + 2) E n ^{( r} , ⁶ , ^z ) = exp [^{— 1} —4—

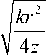
ikr ²

----+ in 6

4 z

^X| ^iJ ( n —1)/2

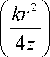
^{+ J} ( n +1)/2

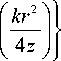
В решении (15) постоянный нормировочный сомножитель

Лexp

. n( n + 2) i

добавлен из тех соображений, чтобы предел функции E_n ( r , 6 , z ) при стремлении z к нулю был равен выражению

E n ( r , 6 , z ) = exp( in 6 ).

В этом нетрудно убедиться, используя асимптотику функции Бесселя в выражении (15) при больших значениях x :

J V ⁽ x ) ~

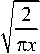
vn x -

^^^^^^B

П

Xa,, X и при условии, что tg ф =---= —, где ф - угол на-

2nY п r0

Таким образом, световое поле (15) можно сформировать, осветив плоской волной с неограниченной апертурой спиральную фазовую пластинку с функцией пропускания (16).

В другом предельном случае, когда z стремится к бесконечности ( 1^0 ), функция (15) будет иметь асимптотику:

i-Jut n ^/2 exp - i ^{п (} n ^{+ 2)} + in 9

E_n ( t ^ 0, 9 ) -------------- ^L 4 --------J . (1₈)

2 n /2 Г I ^{n + 1} I

I 2 J

При получении выражения (18) воспользовались первым членом разложения функции Бесселя в ряд при малом аргументе ( x^0 ):

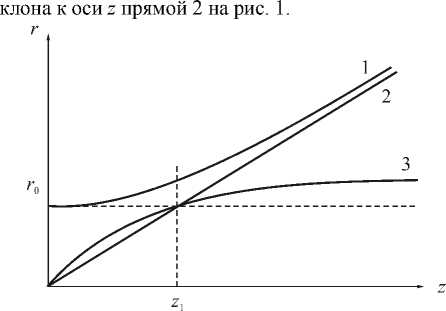
Рис. 1 Зависимость эффективного радиуса пучка от расстояния вдоль оптической оси для: гауссового пучка (кривая 1), параксиального бесселевого пучка (кривая 2) и чистого вихря (кривая 3)

^J m ^{( x} ) ~

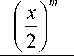
Г ( m + 1)

.

Из уравнения (18) видно, что при W0 функция E_n ( t , 9 ) также стремиться к нулю как t n/² .

Интенсивность моды (15) имеет вид:

Из рис. 1 видно, что при малых z<0 , наоборот, расходимость светового поля (15) наибольшая из трех рассматриваемых полей.

3. Гипергеометрические моды

I n ⁽ r , z ) = E n ⁽ r , ⁹ z ⁾² = у ^{[ J} ( ² n -1)/2 ⁽ t ) ^{+ J} ( ² n +1)/2 ⁽ t ) ]

Функции (15) - частный случай (однопараметрическое семейство) двухпараметрического семейства функций, являющихся решением уравнения (1) в цилиндрических координатах. Эти ГГ моды являются полным ортогональным базисом и сохраняют

Из уравнения (20) видно, что всегда (кроме начальной плоскости z=0 ) при t=0 I_n ( t ) =0 , то есть на оптической оси z всегда будет ноль интенсивности. Это является характерным признаком наличия в световом поле оптического вихря или фазовой сингулярности [13].

Из уравнения (20) с помощью рекуррентных соотношений для функции Бесселя можно получить выражение для производной:

свою структуру в системе координат вида x = rj"z cos 9,

< y = r'Jz sin 9 ,                                   (25)

ГГ моды имеют следующий вид [2]:

^ - n + i y-2

E y n ( r , 9 , z ) =-------- п

exp ^ (3 n - 1 + i y ) x

dI n ⁽ t )           2             2

dt      Л n ^{[ J} ( n -1)/2 ⁽ t ) J ( n +1)/2 J .

Из уравнения (21) видно, что картина интенсивности при любом z имеет кольцевой вид (n+0) и радиус первого основного кольца с максимальным значением интенсивности можно найти из уравнения:

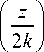
Г n + i y + 11Г          x

I 2 J

x-------iF

Г ( n + 1)^{1 1}

n + 1 - i Y , , ir I ---2--- , n + 1; — I exp( in 9 ),

^J ( n -1)/2 ⁽ t ) = J ( n +1)/2 ⁽ t ).

где - ro< у <да - действительное число, Г( х ) -

Пусть в уравнении (22) первый (наименьший) корень равен t=t_0n , тогда радиус первого светлого кольца в картине интенсивности (20) будет равен:

гамма-функция, 1 F 1 ( a,b;x ) - вырожденная (или конфлюэнтная) гипергеометрическая функция:

r 0 n

1 2 1 0 n X z

П

да

1 F 1 ^{( a} , b ; x ) = E k =0

Г ( a + k ) Г ( b ) x^k Г ( a ) Г ( b + k ) k ! ^.

Существует связь между функцией (27) и функцией Бесселя:

Из сравнения выражения (23) с (6) и (8) можно заключить, что моды (15) имеют самую слабую расходимость из известных параксиальных мод (смотри рис. 1) при z > z i , где

/ X V

I x I __ix e i ^x

( 2 J

J _v( x ) = ^^----- ,F ( v + 1/2, 2 v + 1, 2 ix ).

^v       Г ( v + 1) ¹¹

^z 1

z 0

2 1 0 n ’

Физически световые поля с комплексной амплитудой вида (26) можно сформировать, освещая не-

ограниченной плоской волной амплитудно-фазовый транспарант с функцией пропускания:

r i* ^-'

E _т n ( r , 6 , z = 0) = —— exp( in 9 ).                 (29)

2 n

При r=0 в уравнении (29) возникает особенность, во избежание которой положим Y=-i, тогда вместо (29) получим функцию пропускания фазового транспаранта, отличающуюся от функции пропускания спиральной фазовой пластинки (16) только постоянным множителем:

E - . ( r . 9 ) = ^

2п

.

Поэтому функции (15) должны совпадать с ГГ модами (26) при Y=-i (хотя параметр y в выражении (26) должен быть действительным). Покажем, что это действительно так. Положив в выражении (26)

Подбором значений комплексных коэффициентов C n в выражении (35) можно оптически формировать распределения интенсивности заданного вида, которые при распространении вдоль оптической оси будут сохраняться с точностью до масштаба. Оптически сформировать поле с распределением интенсивности вида (35) можно, осветив неограниченной плоской волной амплитудно-фазовый транспарант с функцией пропускания вида:

N

T ( r , 9 ) = Z C n exp( in 9 ).                      (36)

n =- N

Заметим, что световые поля в дальней зоне дифракции, ограниченные при z=0 одинаковой апертурой V , имеют одинаковые фазовые скорости распространения. Действительно, распределение интенсивности в дальней зоне дифракции зависит от отношения k ^ /z :

Y=-i , получим:

^E -in ⁽ r , ⁹ z ) = ™^eXP

2 п

i 3 n n

- x n /2    ,        .

kr ² ।      । n + 2 ।

-- Г --- x

2 z J I 2 J

I n fe n)

k

— exp z

ik ( E ² +П ²) 2 z

x

Г           ikr¹ ^

------. F n , n + 1; — exp( in 9 ). Г ( n + 1)^{1 1} ( 2         2 z J

^x Jj f n ^{( x} , y ^)exp

V

- ik ( x E, + y n ) 2 z

dxdy

С учетом выражения (28) при v = (n -1)/2, t = k-, 4 z

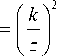
~ Г k E k n

I n I , I z z

.

J ( n -1)/2 ⁽ x ) =

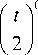
e ^{- it}

Г

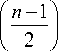
₁ F ( n /2, n ; 2 it )

и рекуррентного соотношения для гипергеометрической функции

₁ F ( n /2, n + 1; 2 ix ) = I — + 2 1 ₁ F ( n /2, n ; 2 ix ),      (33)

I dx J

получим вместо (31) выражение:

E-^ (t, 9) = (2n) 1 ^ exp -iП(3n4- 2) x tje exp (it + in9) [iJ(n-1)/2 (t) + J(n+1)/2 (t)] .

Однако, в отличие от (35), эффективный радиус всех световых полей с конечной энергией и ограниченных областью V в дальней зоне, как видно из (37), расходится линейно с расстоянием ( r~z ), а гипергеометрические моды расходятся пропорционально квадратному корню из расстояния( r ~ z[z ).

Линейная комбинация гипергеометрических мод (35) обладает угловым орбитальным моментом (УОМ) [15,16].Проекция на оптическую ось z вектора углового орбитального момента сохраняется при изменении z , и ее можно вычислить при z= 0. В соответствии с выражением для УОМ [16] для проекции на ось z получим:

i [Г E ( r , 9) — E ‘ ( r , 9 ) rdrd 9

J =           d9

® JJ | E ( r , 9 ) |² rdrd 9

Функция (34) отличается от функции (15) только нормировочным сомножителем ( 2 п)^-1( -1 ) ⁿ .

4. Свойства чистых вихрей

ГГ моды или чистые вихри обладают интересными свойствами. Все моды независимо от величины номера n распространяются с одинаковыми фазовыми скоростями. Это свойство отличает ГГ моды от мод ЭГ, ЛГ, АГ. Это означает, что любая линейная комбинация мод (15) будет сохранять свою структуру с точностью до масштаба ( z>0 ):

где E ( r, 6) - комплексная амплитуда светового поля, удовлетворяющая уравнению (1), и - циклическая частота света. Подставляя выражение (36) в уравнение (38), получим проекцию вектора УОМ для суперпозиции гипергеометрических мод:

N

Z nC n l²

т _ n =- N ________

^J z = N

» £ C n l²

n =- N

.

I ( r , 9 , z ) =

N

Z C n E n ( r , 9 , z )

n =- N

= I

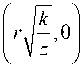
Из уравнений (38) и (39) видно, что хотя гипергеометрические моды обладают бесконечной энергией, нормированный угловой орбитальный момент у них конечен.

Ненормированный УОМ гипергеометрических мод – бесконечный, но плотность момента в каждой точке пространства – конечна. Измерить УОМ светового поля можно с помощью специального дифракционного оптического элемента, функция пропускания которого пропорциональная линейной комбинации угловых гармоник (36) [17].

5. Результаты численного моделирования распространения чистых вихрей и их суперпозиций

Моделировать распространение световых полей вида (35), представляющих собой чистые вихри и их суперпозиции, сложно из-за бесконечного радиального размера таких полей.

Однако, если взять радиус поля достаточно большим, то фактическая ограниченность поля не будет существенно сказываться на его центральной части. Кроме того, моделирование распространения ограниченных вихрей [14] позволяет предсказать поведение полей, формируемых с помощью спиральных фазовых пластинок и дифракционных оптических элементов.

Моделирование непараксиального распространения поля (36) проводилось на основе разложения входного поля по сферическим волнам:

го

F ( u , v , z ) = ^-^- j f f ( x , y ) X

2n

-го exp( ikR) (1

x         ik - d x d y

R2   (

R = ^(x - u)2 + (y - vУ + z2 .(40)

При моделировании использовались следующие параметры: размер поля 5 x 5 мм, число отсчетов в выходном поле 512x512. На рис. 2 показаны результаты моделирования распространения чистых вихрей различных порядков.

Рис. 2. Распределение интенсивности при распространении чистых вихрей порядков n=1, 2, 3, 5 на расстояниях z=5, 10, 20 и 50 мм

На рис. 2 видно, что чем больше порядок вихря, тем шире формируемая им воронка, что согласуется с формулой (23) для радиуса первого светлого кольца поля. Напомним, что радиус воронки пропорционален первому корню функции Бесселя, значение которого возрастает с ростом индекса n . Кроме того, на рис. 2 видно, что растет и яркость первого кольца, а также энергия, которая в нем сосредоточена.

В работе [18] исследовался вопрос использования пучков ЛГ с различными азимутальными индексами для формирования тороидных оптических дипольных ловушек. Было показано, что моды ЛГ с «винтом» более высокого порядка обеспечивают более глубокую потенциальную яму и более компактную концентрацию при фиксированных радиусе тороида и мощности лазера. Анологичные свойства присущи и чистым оптическим вихрям.

На рис. 3 показано распространение линейной комбинации (суперпозиции) чистых вихрей вида exp( i θ )+exp( - 2 i θ ). В первой строке приведены результаты для исходного амплитудно-фазового поля, а во второй строке – для только фазового, т.е. в плоскости z=0 было поле exp{ I arg [exp( i θ ) + exp( - 2 i θ )]}. Последний случай достаточно легко реализовать с помощью фазовых дифракционных оптических элементов. Видно что, как и было предсказано в разделе 4, распределения интенсивности для суперпозиций чистых вихрей сохраняются при распространении вдоль оптической оси с точностью до масштаба. Интересно, что в случае, когда на входе чисто фазовая суперпозиция чистых вихрей, то картина выглядит как уходящие в бесконечность темные каналы постоянной ширины, вместо расходящихся темных клинов как в случае амплитуднофазового поля на входе.

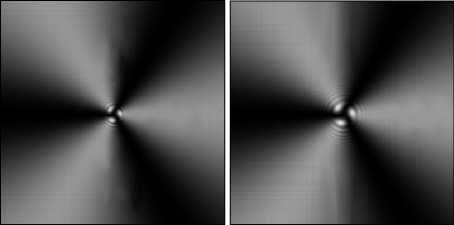
Z=5 мм Z=10 мм

Z=20 мм

Z=50 мм

Рис. 3. Распространение линейной комбинации чистых вихрей вида exp( i θ ) + exp( - 2 i θ ) : распределение интенсивности на расстояниях z=5, 10, 20 и 50 мм для амплитудно-фазового поля на входе (верхняя строка) и только фазового (нижняя строка).

Заключение

В заключении кратко сформулируем полученные результаты.

• •    Получено новое семейство радиально-симметричных линейно-независимых решений параксиального волнового уравнения, которые названы чистыми вихрями и которые обладают слабой расходимостью и одинаковой фазовой скоростью (15).

• •    Сформировать чистые вихри можно, освещая плоской волной с неограниченной апертурой спиральную фазовую пластинку (16).

• •    Показано, что радиус кольца с максимальным значением интенсивности чистого вихря растет

как корень квадратный от расстояния вдоль оптической оси (23).

• •    Показано, что найденные модовые решения являются частным случаем двухпараметрического семейства решений ПВУ, названных гипергеометрическими модами ((26) и (34)).

• •    Результаты численного моделирования подтверждают теоретические выкладки.

Работа выполнена при финансовой поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF REC-SA-014-02) и гранта Президента РФ НШ-1007.2003.01, а также гранта РФФИ 05-01-96505.