Оптические, ИК- и ТГЦ-экраны на основе слоистых структур металл-диэлектрик-полупроводник

В оптическом диапазоне широко используются многослойные экраны (зеркала) и фильтры из прозрачных слоёв, отличающихся показателем преломления (ПП) n = ^s ( to ) [1-11]. Число подобных публикаций весьма велико. Такие плоскослоистые структуры могут служить как зеркала или как многополосные фильтры с окнами прозрачности и непропуска-ния (заграждения) [2–10]. Для проявления селективных свойств толщины слоёв должны быть порядка четверти длины волны, что для оптического диапазона с учётом ПП соответствует сотням нм. Большое значение при этом имеют потери и дисперсия диэлектрической проницаемости (ДП) s ( to ), ухудшающие, как правило, свойства и ограничивающие полосу. Получение сильно селективных свойств на небольшом числе слоёв требует большого различия их ДП. Однако у оптически прозрачных материалов такое различие невелико, как невелико и разнообразие самих таких материалов. Поэтому возникает задача синтеза слоёв с заданными свойствами. Большинство материалов в той или иной степени содержат свободные носители зарядов, т.е. относятся к полупроводникам, полуметаллам и металлам (эта градация сильно зависит от рассматриваемого диапазона и температуры). Параметры полупроводниковых слоёв (концентрации и плазменные частоты) можно менять легированием, оптической и электрической накачкой, а также управлять ими с помощью внешнего магнитного поля, что делает привлекательным использование полупроводниковых плёнок. Кроме того, возможно допирование диэлектрических плёнок металлическими и иными наночастицами с использованием формул смешения типа Бруггемана,

/ М.В. Давидович, И.А. Корнев // Компьютер-

Дж.К.М. Гарнетта и ряда других. В сильном магнитном поле ДП металлических и полупроводниковых плёнок приобретает тензорный характер со свойствами замагниченной плазмы. Такую тонкую плёнку толщины t удобно описывать тензором двумерной проводимости 6 = i tos ₀ ( s ( to ) - I) t , где s ( to ) - ДП плазмы.

В ИК- и ТГц-диапазонах также интересны отражающие экраны, многополосные фильтры, фильтры-поглотители. Такие плоскослоистые структуры можно рассматривать как метаповерхности. В частности, нанесённые на оконное стекло прозрачные в оптическом диапазоне, но сильно отражающие в ИК-диапазоне структуры или тепловые экраны весьма перспективны: зимой они препятствуют излучению тепла из здания, что позволяет существенно экономить на отоплении, а жарким летним днём препятствуют проникновению тепла внутрь. Многослойные тепловые экраны на основе наноразмерных плёнок Cu-SiO 2 , Cu-SiO, Al-SiO 2 , Al-SiO были предложены в работе [12]. Также подобные структуры рассматривались в ряде других работ [13–18]. Использование только плёнок SiO 2 , по-разному допированных для небольшого отличия ПП, в принципе позволяет получить модуль коэффициента отражения, почти равный единице, но требует создания структуры с несколькими десятками периодов, что технически сложно. Использование хорошо проводящих металлов позволяет создавать слои с Re( s ( to ))<0, поддерживающие затухающие моды, но они хорошо прозрачны только в узком оптическом диапазоне, а на низких частотах имеют большую отрицательную мнимую часть и большие потери.

В общем случае мы будем описывать любой слой ДП в форме модели Друде–Лоренца:

е(ю) = eL (ю) - юр / (ю2 - iююc), где еL(ю) - Лоренцев член (без учёта вклада свободных носителей заряда). Он соответствует ДП кристаллической решётки или поляризации атомов, а также поляризации за счёт межзонных переходов (если они есть). Для диэлектрика достаточно для плазменной частоты положить юp=0, что соответствует отсутствию свободных зарядов. Для низких потерь должна быть мала частота столкновений юc, для чего нужны чистые материалы, низкие температуры или компенсация потери путём оптической накачки (в другом диапазоне) полупроводниковых слоёв, т.е. создание структур типа спазеров. В частности, это интересно для ИК- и ТГц-экранов при накачке из оптического или УФ-диапазонов.

Цель данной работы – исследование структур из нескольких слоёв, квазипериодических структур с несколькими разными материалами слоёв и аналогичных периодических структур для получения селективных свойств в оптическом, ИК- и ТГц-диапазонах. При этом для увеличения широкополосности предложено использовать материалы с сильно различающимися и перестраиваемыми (оптически, электрически или за счёт температуры) значениями плазменных частот. Для существенно различных поддиапазонов удобны квазипериодические структуры, в которых большой период содержит несколько периодически расположенных с малым периодом элементов.

Структуры из нескольких слоёв

E-моды и H-моды относительно перпендикулярного слоям направления распространения характеризуются нормированными на Z ₀ = ^ ц ₀ / e ₀ волновыми импедансами р n = k z /( к ₀ е _n ) для E-моды, и р n = к 0 / k zn для H-моды, где k z„ = _v к 2 e _п - к , ² . Дифракция на структуре описывается полной нормированной матрицей передачи a ˆ , равной произведению матриц передачи всех слоёв:

л an

cos ( 6 n )

i sin ( 6 n ) / P n ’ h )

i sin ( 6 n Veh ) cos ( 6 n )

где 6n = kzn tn, tn - толщина слоя. ДП имеет вид еn = en - ien. При возбуждении плоской волной величина kx действительная и определяет угол падения ф = arctan (kx / kz0) , где kz0 = ^к02 - kx . Если же вдоль структуры распространяется плазмон, то величина kx комплексная и определяется из дисперсионного уравнения, которое следует из согласования импедансов вакуума и структуры [19–21]. Соответственно возбуждение плазмона квазиплоской волной тем сильнее, чем меньше коэффициент отражения, который зависит от угла падения. При возбуждении квазимо-нохроматическим пучком с угловым спектром возникает зависимость цветности от угла в отражённом и прошедшем свете [22]. При дифракции возможно условие 6n ® -i |6n |, если en < 0 и к02en - kx < 0 , а диссипация в слое мала, что обычно соблюдается в области плазмоники. В этом случае матрица передачи слоя в пренебрежение диссипацией имеет вид an

cosh (6 n|)        i sinh (6 n |)|p(ne’ h )| i sinh (|6n|) / |pne, h )|       cosh (6 n |)

.

Перемножение соответствующих слоям матриц типа (1) и (2) может для полной матрицы конечной структуры приводить к условиям либо | X |<1 (структура работает как фазовращатель со сдвигом фазы V и фазовым множителем exp(- i V )), либо | X |>1 (структура работает как аттенюатор с множителем exp(-| v| )). Здесь cos( v ) = X = (<2 11 + at₂₂)/ 2 . В общем случае диссипации фазовый сдвиг и множитель комплексные.

При расчёте структур из нескольких слоёв случай | X |>1 может быть реализован в полосе непропускания как при условиях e n <  0 , так и при условиях e n >  0 , а также и при смешанных условиях. При этом на границе полосы имеет место равенство, а в центре | X | максимально. Вне полосы заграждения возникают резонансы пропускания. Такие резонансы на эванес-центных модах известны, например, для периодических структур [23]. Заграждение при всех прозрачных слоях, отличающихся ПП с cos ( 6 _n ) <  1 в периодическом случае, известно как отражение за счёт брэгговских резонансов. При малом числе слоёв (периодов) хорошее заграждение получается при сильном различии ДП (ПП) слоёв.

Вычислив матрицу передачи, имеем коэффициент отражения структуры: R =( Z – 1)/( Z + 1), где введён её нормированный импеданс

Z = <11 + <12/ р

< 21 р + <  22

Уравнение (3) пригодно для обеих поляризаций. Указанный выше аналитический расчёт можно использовать для матриц слоёв (1) и (2) в качестве начального приближения для численной оптимизации, которую удобно проводить из условия

min Z(lЛ12 - 1Л0р),

где | R 0 | ‒ искомое значение модуля коэффициента отражения, а сумма берётся по заданным частотным точкам. Также можно производить численный синтез по сопротивлению (3), а в случае малой диссипации и по значению | X |.

Квазипериодические структуры

Такие структуры имеют число периодов порядка нескольких десятков. Периодичность сильно сказывается на частотной характеристике уже при числе периодов более десяти, а при их числе порядка сорока и более вполне можно использовать дисперсионную характеристику Флоке–Блоха периодической структуры фотонного кристалла (ФК). Последняя определяет фазовый сдвиг ^ = kzd на периоде d. Этот сдвиг можно получить как полную фазу коэффициента прохождения T, рассчитанную с учётом её скачков 2п и делённую на длину структуры. Полосы заграждения (непропускания) имеют место в областях запрещённых зон дисперсии ^(к0). Следует отметить, что запрещённые зоны существуют для структур без диссипации (в них фазовый сдвиг мнимый), а при потерях в них имеет место распространение с большими затуханиями [19–21]. При этом даже если структура почти периодическая, периодичность волн из-за затухания нарушается. Синтез таких структур удобно производить на основе величины X для одного периода. Синтезируемые таким образом структуры с большим числом периодов и слоёв должны затем быть проанализированы как конечные с вычислением коэффициента отражения R и прохождения T. Число слоёв как минимум в два раза больше числа периодов, поскольку простейшие структуры содержат два слоя в периоде. Удобны структуры с тремя слоями в периоде с сильно различающимися плазменными частотами. В частности, один из слоёв может быть диэлектрическим, т.е. с нулевой плазменной частотой. Такие квазипериодические структуры содержат ещё больше слоёв. Интересны структуры типа период в периоде, когда большой период содержит несколько мелких периодов из двух слоёв. Однако для синтеза такие структуры должны быть хорошо прозрачны.

Выполнение структур со многими слоями – технологически достаточно сложная и дорогая операция. Для ИК (тепловых) экранов с большой поверхностью желательно напылять не более двух металлических или полупроводниковых слоёв. Для структур со многими периодами удобно синтезировать периодические структуры, а затем путём оптимизации пытаться корректировать частотные свойства реальной структуры. Итак, для двух или трёх слоёв в периоде начальная оптимизация идёт по двум или трём параметрам. Затем полученные толщины, периоды которых 2 n или 3 n , следует использовать при оптимизации структуры из n периодов.

Тонкие плёнки и структуры с малой толщиной

Если толщина металлического слоя много меньше глубины проникновения 5 , для структур типа ФК удобно использовать методы гомогенизации [21] . Обычно глубина проникновения 5 <<  X . Такой ФК является гиперболическим метаматериалом, т.е. при определённых условиях без учёта диссипации может быть описан двумя компонентами эффективной ДП s xx <0, s zz >0. В длинноволновом пределе для ФК с металлическим и диэлектрическим слоем в периоде d = t m + t d имеем значения диагональных компонент тензора эффективной ДП

- ¹

Sm^m , Sdtd     _i | Smtm , Sdtd 1

S xx         T + T , S ZZ I 1 ~ 1 I d d I d d )

.

При учёте пространственной дисперсии для этих величин возникает зависимость от kx, т.е. от угла па- дения. В случае тонкого металлического слоя tm<< X его удобно описать поверхностной проводимостью ° = i®s0(sm-1). Для такого слоя имеем

Л a ° n

( ° Z 0 ) 1

Естественной плёнкой, имеющей двумерную проводимость, является графеновый лист. Его проводимость приведена в ряде работ, например, в [24]. Можно использовать как её скалярное значение, так и тензорное значение. В последнем случае моды становятся гибридными и следует использовать матрицы 4×4. Такие матрицы в оптике известны как матрицы Берремана [25]. Вид матрицы зависит от того, в каком порядке сшиваются компоненты полей. Если принять порядок компонент ( E x , H y , – E y , H x ), матрица анизотропно проводящего листа примет вид

	■ 1 0 0      0 "
аа =	Z 0 ° ny 1 - Z 0 ° nz 0	.                         (5)
° m	0 0 10
	_- Z 0 ° nz 0 Z 0 ° nz 1 _

Удобно использовать нормированную (безразмерную) проводимость | = Z 0 ° n . В случае диэлектрических однородных слоёв и анизотропно проводящих листов классическая матрица 4×4 слоя имеет блочнодиагональную структуру с матрицами E-волн и H-волн (1) на диагоналях. Кроме классических матриц типа (1), можно использовать волновые матрицы передачи и матрицы рассеяния. Эти матрицы связывают амплитуды волн различных направлений. Однако это не приводит к выигрышу в скорости для алгоритмов. Сконструировать наноразмерную металлическую плёнку с тензорной проводимостью можно, например, выполнив в ней 2D-перфорацию в виде ориентированных щелей [17]. Продольная проводимость вдоль щелей будет индуктивной, тогда как поперечная может стать ёмкостной. Структуры с такими плёнками работают как поляризаторы. При падении волны одной поляризации возникают обе как в отражённом, так и в прошедшем свете.

Оптически прозрачные ИК- и ТГц-экраны

Для получения оптической прозрачности должно выполняться несколько условий. Первое – плазменные частоты слоёв должны лежать в ИК- или ТГц-диапазонах, а в интересующем оптическом окне находится зона пропускания. Второе – толщины металлических слоёв должны быть порядка десятка нанометров и менее, т.е. металлические слои должны быть прозрачными в оптическом диапазоне, а запрещённые зоны – не попадать в область окна. Третье – полупрозрачные в оптике металлические слои с толщинами в десятки нм и четвертьволновыми и менее слоями диэлектрика образуют структуру с большим коэффициентом отражения в ИК- и в более длинноволновой области, где Re(sxx)<0. Синтез таких структур возможен по полосам заграждения при пренебре- жении диссипацией с использованием величины X. Удобными параметрами оптимизации могут служить плазменные частоты, толщины слоёв и ДП sL. Для полной оптимизации структуры из N периодов с двумя слоями в периоде таких параметров 3N, если длина периода фиксирована, и 4N – если нет. Если же использовать только диэлектрические слои, для хорошего заграждения необходимо большое число периодов. Поэтому удобна предварительная оптимизация периодической структуры. После такой предварительной оптимизации следует рассчитывать параметры R и T с учётом диссипации. В малой окрестности полученных значений можно провести корректирующую оптимизацию по R или T.

Рассмотрим предварительную оптимизацию в случае двух слоёв. Если оба слоя прозрачны, то X = cos(0i)cos(02)- Zi,2sin(0i)sin(02), где введена безразмерная величина Z1,2 = (pi/p2 + pVp^/2. Индексы у импедансов опущены. Очевидно, значения X = ±1 соответствуют фазовым сдвигам ^ = ±л, т.е. границам зон непропускания. Удобно положить 01 = 02. Тогда X =1- (Zi,2+i)sin2(0i). В полосе заграждения должно быть sin2(0i)>2/( Z +1). Определяя Zi,2 = (pi/p2 + р2/р1)/2 через плазменные частоты и ДП sL1, sL2, ищем граничные частоты, где выполняется равенство. Сдвиг частот определяет толщина слоя. Если же первый слой прозрачный, а второй нет, то р2 = i |р2| для обоих типов поляризаций, cos(02) = cosh(|02|), sin(02) = - i sinh(|02|), поэтому Zi,2 = i(|p2|/Pi —Pi/|P2l)/2 = iZ , а определение границ полосы непропускания следует проводить на основе уравнения cos (0i ) =

± i + Z sin ( 0 _i) sinh (| 0 ₂|) cosh(| 0 ₂|)

Оно упрощается, если в этой полосе | р ₂| ® p _i. Следует отметить, что все величины зависят от угла падения (величины k x ), поэтому увеличение угла падения может приводить к условию (6) даже для положительной ДП, если 0 < s 2 <  i.

Для трёх слоев в периоде имеем X = A – B – C , где

A = cos ( 0 _i ) cos ( 0 ₂ ) cos ( 0 3 ) ,

B = Z i,2 sin ( 0 3 ) sin ( 0 2 ) cos ( 0 3 ) ,

C = sin (03 )x p2 cos (0i) sin(02 ) + pi sin(0i)cos (02) p2

.

В области заграждения либо все три величины 0„ действительные, либо только две, либо одна. Традиционно рассматриваемые задачи относятся к обратным задачам [26]. Можно рассматривать различные подходы к синтезу и оптимизации, в том числе и по значениям X для непериодической структуры, для одного периода структуры или по значению Xm = Tm (X) для структуры из m периодов. Отличие точного синтеза от синтеза по X в том, что использу- ется полином Чебышева первого рода порядка m. Поскольку Tm(±i) = (-i)m, синтез по X правильно определяет границы полос заграждения, а при больших m результат синтеза для бесконечной структуры близок по частотным характеристикам к конечной структуре. Результаты для оптимальных ИК- и ТГц-экранов в виде 3 мм стеклянной подожки с четырёхслойной ме-талл-диэлектрик структурой приведены на рис. 1.

\Т\ 1.0Е+0'

l.OE-b

l.OE-2-i

1.0Е-3-.

1.0Е-4-,

1.0Е-5л

l.OE-бз

1.0Е-7ч

ЕОЕ-8^

l.OE-Sh

l.OE-1 Оз

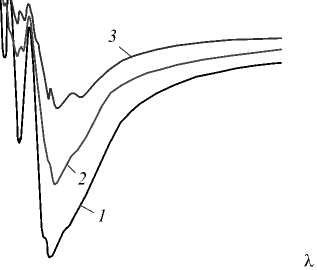
1.0Е-5 1.0Е-4 1.0Е-3 1.0Е-2 l.OE-1 1.0Е+0

Рис. 1. Коэффициент прозрачности по мощности в зависимости от длины волны в см для двухслойной структуры из металлической пленки толщины 30 нм и слоя SiO 2 толщины 300 нм при четырёх периодах, расположенной на стеклянной подложке 3 мм: алюминий (кривая 1), никель (2), хром (3)

На рис. 2 даны результаты для такой структуры с двумя, тремя и четырьмя периодами.

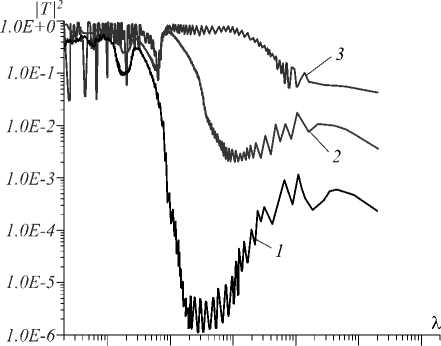
1.0Е-5 1.0Е-4 1.0Е-3 1.0Е-2 l.OE-1 1.0Е+0

Рис. 2. Прозрачность по мощности в зависимости от длины волны (см) при ® р = 1,9х10¹⁶ Гц, ® с = 10 1 Гц, толщине металла 15 нм, толщине подложки SiO 2 50 нм для четырёх периодов (кривая 1), трёх периодов (2) и двух периодов (3)

Для экранов с металлическими пленками подавление в ТГц-диапазоне тем больше, чем больше периодов и, соответственно, толщина экрана. На рис. 3 приведена прозрачность по мощности для структуры InSb-SiO 2 -Al из десяти слоёв. InSb характеризуем ДП i7,5 и to p = 6xi0ⁱ² Гц, для Al взято to p = i,45xi0ⁱ⁶ Гц.

Наиболее дешёвыми и технологичными ИК-экранами являются однослойные металлические по- крытия на стекле. Для оптической прозрачности толщина металлической плёнки должны быть существенно меньше оптической глубины проникновения, т.е. порядка 20‒30 нм. Коэффициент отражения такой плёнки проще всего получить методом трансформации импеданса. Именно трансформируя волновой импеданс вакуума р0 диэлектрическим слоем к границе с металлической плёнкой, получаем входной импеданс

ро + iрd tan (9d) р in = р d                 , ч .

рd +1 ро tan (9d)

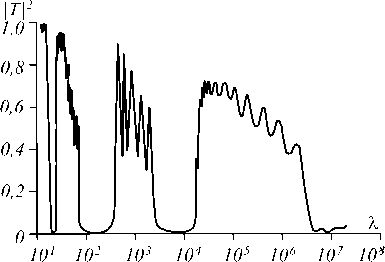
Рис. 3. Результаты вычисления прозрачности по мощности в зависимости от длины волны (нм) структуры из 10 периодов InSb-SiO 2 -Al c толщинами 100 нм и 400 нм и 5 нм

Далее трансформируем этот импеданс металлической плёнкой, получаем ри = р m

Pin + iрm tan (9m ) рm + Iр^ tan (9m )

Здесь индексами m и d обозначены параметры металла и диэлектрика. Следует учесть, что в интересующей нас ИК-области для хороших металлов диссипация мала, поэтому 9 m ® - i |9 m |, р m ®i |р m |. Имеем R = (рn —р0)/(рn +р0), при этом в силу малости толщины плёнки диссипацией в ней можно пренебречь, и получаем |T|2 = 1–|R|2. Можно также положить tan(9 m) ® - i tanh(|9 m |) ® - i |9 m |. Для упрощения удобно описать плёнку поверхностной проводимостью. Тогда имеем рк = [р‘п| + кооtm (sL -1-Ю2 /to2)] 1.            (12)

В этих формулах величина 9 d большая, а импеданс (11) осциллирует с частотой и углом падения, поэтому результат желательно усреднить. Результат показывает, что медная или алюминиевая плёнка позволяет уменьшить прозрачности до 20 %.

ТГц-экраны и фильтры

Используя плазмонную запрещённую зону при отрицательной ДП s <0 проводящего слоя в ТГц-диапазоне или фотонную запрещённую зону, когда плазменная частота достаточно низкая и s > 0, можно получить хорошее заграждение для структуры из 2‒3 десятков периодов. Однако такая структура имеет много узких полос пропускания в ИК- и оптическом диапазоне. Изменяя толщины слоёв в таких структурах, получаем пропускающие ТГц-фильтры. Это же относится к ИК-диапазону. В нём желательны материалы со значениями плазменных частот порядка 1013‒1015 Гц, для чего можно использовать полуметаллы и сильно легированные полупроводники.

При использовании хорошо прозрачных диэлектрических слоёв их толщины при брэгговских резонансах в ТГц-диапазоне составляют порядок сотен мкм, а число периодов должно существенно превышать 10. Такая структура с 20 периодами имеет длину порядка нескольких мм. В оптическом диапазоне она имеет весьма изрезанную частотную характеристику. При усреднении по белому спектру будет иметь место частичное пропускание. Поэтому удобно использовать более тонкие слои с плазменными частотами, лежащими вблизи полосы. Области плазмоники ( s '<-1) соответствуют частоты to c < to < to p / ^s _L + 1 , тогда как область to « to p / ^/s L или «эпсилон, близкое к нулю» соответствует сильному затуханию в слое, когда для его ПП имеем n ® ( 1 - i ) / Vs'' / 2 .

Оптические экраны

Пример расчёта прозрачности оптических экранов с десятью периодами и двумя слоями в периоде дан на рис. 4.

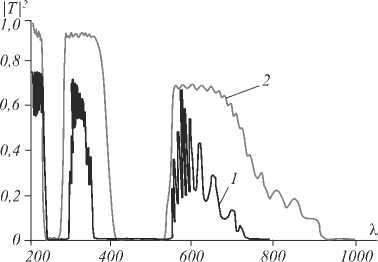
Рис. 4. Оптический и ИК-экран из m периодов металла t m =10 нм и диэлектрика t d =200 нм для е а =3. Кривая 1 - Ag, m=10, кривая 2 – Al, m=20

Рассмотрены структуры c m- периодами металл–диэ-лектрик. Для них имеют место полосы заграждение в УФ-диапазоне, а также полоса заграждения в диапазоне красного, ИК- и части ТГц-диапазона. Увеличение числа слоёв увеличивает заграждение в длинноволновой области, в том числе и за счёт диссипации.

Отличие структур с полупроводниковыми слоями (рис. 3) и металлическими слоями (рис. 4) состоит в сдвиге областей плазмонных запрещённых зон по частоте в силу разных плазменных частот, при этом для первых возможно окно прозрачности в ИК-диапазоне, тогда как вторые являются тепловыми экранами.

Заключение

В работе показана возможность фильтрации и заграждения в определённых широких полосах оптического, ИК- и ТГц-диапазонов на основе многослойных структур металл–диэлектрик–полупроводник.

Рассмотрены структуры из нескольких слоёв и квази-периодические структуры типа два слоя и три слоя в периоде с числом периодов порядка 10 и более. Предложен метод синтеза по величине X , определяемой матрицей периода или полной матрицей структуры. Рассмотрены методы создания полос заграждения с использованием как прозрачных, так и непрозрачных слоёв, для чего предложен приближённый синтез с подборкой требуемых плазменных частот слоёв путем допирования. Рассматриваемые задачи относятся к обратным, поэтому предварительный синтез требует численной оптимизации с учётом диссипации.