Оптические моды в линейных массивах диэлектрических сферических частиц. Численное исследование

В настоящее время растущий интерес привлекают к себе прямые цепочки и другие низкоразмерные сруктуры сферических наночастиц, способные передавать оптическую энергию из одной точки пространства в другую [1–3]. Под воздействием внешнего электромагнитного излучения определённой частоты в таких структурах могут возникать коллективные оптические моды, называемые плазмонами, если частицы металлические, и поляритонами, если частицы диэлектрические. Эти возбуждения представляют собой суперпозицию колебаний векторов поляризации вещества и электромагнитного поля. Вообще говоря, эти возбуждения являются затухающими, поскольку оптическая энергия может поглощаться веществом частиц или излучаться в пространство в виде свободных фотонов. Однако если поглощение энергии веществом слабо, а частота моды лежит в зоне проводимости, то есть в области частот, где излучение свободного фотона невозможно, то мода может распространяться вдоль цепочки почти без по- терь энергии. Таким образом, цепочка наночастиц способна вести себя как волновод высокой добротности, что может быть использовано в различных микро- и наносистемах. Переносимая энергия может, например, возбуждать молекулы или стимулировать химические реакции на другом конце волновода.

Как нам известно [2, 3], первый нановолновод, способный передавать энергию на расстояние в пределах 100 нм, представлял собой линейную цепочку сферических серебряных или золотых частиц. При возбуждении плазмонного резонанса на частице на одном конце волновода энергия по очереди передаётся всем частицам в цепочке. Однако с ростом длины цепочки эффективность переноса энергии заметно падает в связи с поглощением энергии электронами проводимости.

Чтобы избежать потерь энергии, связанных с поглощением, было предложено использовать цепочки не из металлических, а из диэлектрических частиц. В диэлектрическом волноводе, где поглощение энергии слабо, основные потери связаны с излучением энергии в виде свободного фотона. Однако радиационные потери энергии могут быть практически полностью исключены, если частота возбуждения лежит в зоне проводимости. В этой области частот излучение свободного фотона бесконечной цепочкой невозможно в связи с законом сохранения импульса, поэтому естественно, что на частотах, лежащих в зоне проводимости, потери энергии на излучение в конечной цепочке будут минимальны.

Чтобы проиллюстрировать это, рассмотрим бесконечную цепочку с периодом a , расположенную вдоль оси Oz . Все оптические возбуждения бесконечной цепочки характеризуются различными значениями квазиволнового вектора q, лежащими в интервале - π/a < q < π/a [4]. Если частота возбуждения такова, что волновой вектор к = ш/c свободного фотона этой частоты меньше значения квазиимпульса q , то излучение фотона запрещено законом сохранения импульса. Таким образом, для частот, удовлетворяющих условию ω/c < π/a , существуют две ветви проводящих мод, не подверженных радиационным потерям:

⁽ - ⁿ-<_q< - ^{ш )} . ^{( ш}<д<^{п )} . a cc a

Критерий ω/c < π/a равносилен условию, что расстояние между частицами a должно быть меньше половины длины волны свободного фотона частоты ω :

а<|. (1)

где А = 2 с;/(ш [5—9].

Стоит заметить, что металлические цепочки легко удовлетворяют критерию (1), поскольку при периоде цепочки порядка a ~ 30 нм частоты проводящих плазмонных мод лежат в спектре видимого света, длина волны которого составляет несколько сотен нанометров [2, 3]. Таким образом, в металлических волноводах радиационные потери энергии практически отсутствуют, и преобладающими являются потери, связанные с поглощением.

Волноводы из диэлектрических материалов могут удовлетворять критерию (1), если показатель преломления материала достаточно велик. Как показано в работе [9], где рассмотрена модель осциллирующих диполей, проводящие моды, удовлетворяющие критерию (1), действительно могут существовать в цепочках частиц, сделанных из таких материалов, как TiO2, ZnO или GaAs. При этом показатель добротности проводящих поляритонных мод стремится к бесконечности по мере роста числа частиц в цепочке. К тому же, моды у границы зоны проводимости обладают групповой скоростью, близкой к нулю. Поэтому цепочки диэлектрических частиц демонстрируют наличие медленных оптических мод так же, как и другие системы, исследованные теоретически или экспериментально [10–15].

Для переноса энергии по цепочке диэлектрических частиц наибольшее значение имеют моды, обладающие наибольшим временем жизни (максимальным показателем добротности). В настоящей работе исследована зависимость показателя добротности этих мод от числа частиц в цепочке на основании формализма многократного рассеяния [16, 17, 7]. Как будет показано ниже, достаточно точные результаты можно получить в дипольном приближении, в котором численные расчёты могут быть произведены быстро.

В разделе 2 мы описываем формализм многократного рассеяния и его приложения к исследованию собственных решений уравнений Максвелла для цепочки частиц. В разделе 3 представлены полученные численно зависимости показателя добротности от числа частиц в цепочке, а также исследовано влияние приближения. В разделе 4 мы приводим наши выводы.

• II.    Формализм многократного рассеяния в изучении цепочек частиц

В этой работе мы используем формализм многократного рассеяния [16, 17], который был развит для исследования распространения электромагнитных волн в системах сферических диэлектрических частиц, распределённых в пространстве произвольным образом. Основная идея этого формализма заключается в том, что волна, рассеянная каждой частицей, представляется в виде суперпозиции сферических векторных гармоник. Каждая такая гармоника характеризуется угловым моментом n = 1.2. ... и его проекцией на ось Oz: m = -n. .... n. Интенсивность каждой гармоники в рассеянной волне ха- рактеризуется парциальными амплитудами almn , blmn , которые отвечают двум поляризациям электромагнитной волны (здесь l = 1, ..., N — номер частицы). Парциальные амплитуды рассеянной волны могут быть выражены через парциальные амплитуды plmn , qml n падающей волны с помощью коэффициентов рассеяния Ми an, bn и коэффициентов переноса Ajmlnμν и Bmjlnμν :

l        N   nmax n amn- + Е ЕЕ AUj+ a n    j= 1(=l) n =1 m = -n

N  n max n

+ E E E Bmn-v b-v  pmn, j=1(=l) n =1 m = -n

N  n max   n

l

^r.

bmn                        jl j b + / < / < 7 ^ mmv^v'J++ n    j =1(=l) n=1 m=-n

n

N

n max   n

+ У У У BjLuvjL = Mm n-  (2)

mnμν μν mn j =1(=l) n=1 m=-n

Коэффициенты переноса и коэффициенты Ми являются функциями частоты. При этом коэффициенты переноса определяются взаимным расположением частиц, тогда как коэффициенты Ми характеризуют их размер и показатель преломления.

В строгой формулировке задачи индекс n в уравнении (2) пробегает все целые значения от единицы до бесконечности, однако на практике сумму по этому индексу приходится обрезать на каком-то максимальном значении n _max .

В дальнейшем мы будем рассматривать собственные поляритонные моды цепочек частиц, удовлетворяющие однородной системе уравнений l        N nmax n amn + E У У AU * + mnμν μν

a n    j=1(=l) n=1 m=-n

N  n max n

+ У У У BjU bU = 0 , mnμν μν

• j =1(= l ) n =1 m = -n

l        N nmax n m + E EE j ^j + mnμν μν

• ⁿ    j = 1(= l ) n =1 m = -n

N  n max n

• + E EE B mln-vj =о ,  (3)

j =1(=l) n=1 m=-n которая получается из системы уравнений (2) в отсутствие падающей волны. Эта система уравнений имеет нетривиальные решения только на дискретном множестве частот za = wa — iYa, для которых определитель системы уравнений (3) обращается в ноль (мнимая часть этих частот определяет время затухания моды за счёт потерь энергии). Показатель добротности моды с частотой za обычно определяется так:

Q a = W a - (4) 2 Y _a

Таким образом, наша задача заключается в том, чтобы вычислить собственные частоты z a . При этом расчёты могут быть произведены только в рамках какого-то приближения, ограничивающего число уравнений в системе (3). Было рассмотрено шесть возможных вариантов таких приближений. Самые простые варианты состоят в том, чтобы положить все парциальные амплитуды равными нулю, кроме a^l_m 1 (вариант (A)) или b ^l _m 1 (вариант (B)) [7]. Другие варианты заключаются в том, чтобы положить П max = 1 (C), П max = 2 (D), n max = 3 (E), n max = 4 (F). Сравнивая результаты этих шести подходов, мы обнаружили, что приближения (A) и (B) позволяют достаточно точно вычислить частоты (действительной части), тогда как приближение (E) n _max = 3 даёт достаточно точное значение показателя добротности.

В настоящей работе мы исследуем конечные линейные цепочки идентичных сферических частиц, расположенных вплотную друг к другу и состоящих из трёх различных диэлектрических материалов: ZnO ( n r = 1 , 9), TiO ₂ ( n r = 2 , 7) и GaAs ( n r = 3 , 5). Аксиальная симметрия цепочки приводит к сохранению проекции углового момента, что формально следует из того, что при m = ц коэффициенты переноса A ^l _m ^j _nμν и B _m ^lj _nμν равны нулю. Поэтому систему уравнений (3) можно разбить на несколько подсистем, характеризуемых определённым значением m . Любая из этих подсистем может быть записана в матричном виде

MM _m ( z ) x = 0 .

Вектор-столбец x содержит парциальные амплитуды almn, blmn, а MMm (z) — зависящая от частоты матрица, диагональные элементы которой представляют собой обратные коэффициенты Ми 1/¯an и 1/bn, а недиагональные элементы содержат коэффициенты переноса Almj nmν , Bmlj nmν .Вна-стоящей работе мы рассматриваем только моды с m =0 (продольные, l-моды) и с m =1 (поперечные, t-моды).

Как уже было сказано, частоты собственных поляритонных мод цепочки могут быть найдены лишь численно из условия вырожденности матрицы однородной системы уравнений (3). Для этого мы использовали алгоритм Ньютона–Рафсо-на, представляющий собой метод последовательных приближений. Каждое следующее приближение z n +1 получается из предыдущего z n по формуле

f ( z n )

^{z n +1 = z n} df ( z n ) /dz ^, где f ( z ) — минимальное по модулю собственное значение матрицы M _m ( z ) [7].

• III.    Исследование цепочек частиц

Ниже приводятся результаты исследования линейных цепочек сферических диэлектрических частиц, расположенных вплотную друг к другу (при этом расстояние между частицами минимально, поэтому интервал частот, удовлетворяющих условию (1), наиболее широк). Мы полагаем радиус частицы равным единице, при этом межчастичное расстояние равно a =2. Поскольку частоты и темпы затухания возбуждений обратно пропорциональны размерам частицы, можно легко вычислить их для любого a .

В приближениях (A) и (B) численный расчёт приводит к двум разным собственным поляритонным модам, обладающим наибольшими временами жизни и отвечающим нижним резонансам Ми в коэффициентах ¯ a ₁ и b ₁ соответственно. Мы будем называть эти моды a — и b -модами. Обе эти моды получаются также в приближении (C), в котором уравнение (3) содержит коэффициенты a ¯ 1 и b 1 одновременно. Частота b -моды меньше частоты a -моды (см. также [7]), причём включение в уравнение (3) мультипольностей более высокого порядка (приближения (D) — (F)) даёт к значениям частот лишь малую поправку, не превышающую 1%. Кроме того, показано, что частоты a — и b -мод почти не зависят от числа частиц в цепочке. Даже для цепочки, содержащей только 10 частиц, эти частоты могут быть найдены с достаточной точностью.

В табл. 1 приведены значения безразмерного параметра λ/ 2 d для продольных и поперечных a — и b -мод и показателей преломления частиц n _r = 3 , 5, 2 , 7, 1 , 9, соответствующих веществам GaAs , TiO 2 иZnO (здесь λ = 2 πc/ω — длина волны моды, d — диаметр частиц, равный межчастичному расстоянию). Когда этот параметр больше единицы, мода является проводящей. Из табл. 1 можно заключить, что все низкочастотные a — и b -моды для GaAs и TiO 2 являются проводящими, тогда как для ZnO заведомо проводящей является только поперечная b -мода (для продольной a -моды параметр λ/ 2 d <  1, а на счёт поперечной a -моды и продольной b -моды нельзя точно сказать, являются ли они проводящими или нет, поскольку эти моды расположены слишком близко к порогу λ/ 2 d =1).

III.1. Частоты проводящих мод

Таблица 1

Параметр проводимости для мод, обладающих наибольшими временами жизни

Материал λ/ 2 d	GaAs		TiO 2		ZnO
	l -мода	t -мода	l -мода	t -мода	l -мода	t -мода
a -мода	1 , 668	1 , 869	1 , 312	1 , 482	0 , 994	1 , 168
λ/ 2 d	l -мода	t -мода	l -мода	t -мода	l -мода	t -мода
b -мода	1 , 299	1 , 869	1 , 077	1 , 303	0 , 949	≈ 1

• III.2.    Показатели добротности

Исследование b -мод в цепочках частиц, состоящих из GaAs, показало, что показатели добротности этих мод зависят от числа частиц по закону

Q ( N ) к CN ³ , (5)

что соответствует результатам более ранних исследований. Физическая природа этой зависимости была объяснена на основании анализа времени жизни моды в конечной одномерной фотонной системе у границы зоны [9, 18, 19] (см. также более ранние теоретические и экспериментальные работы [10–15]).

Хотя выбор приближения почти не влияет на точность при вычислении собственных частот, он оказывает существенное влияние на точность вычисления показателя добротности. Как показано на рис. 1, зависимость Q (N) может быть представлена в виде (5) в любом приближении, но коэффициент C зависит от выбранного приближения. Поскольку для GaAs различие между значениями показателя добротности, вычисленными в приближениях nmax = 3 и nmax = 4, составляет около 0,3%, а для TiO2 и в ZnO оказывается даже меньше, мы предполагаем, что приближение nmax = 3 даёт достаточно точную оценку показателя добротности для любого материала. Результаты, приведённые ниже, для GaAs даны в приближении nmax = 3, а для TiO2 и ZnO — в приближении nmax = 2, так как для этих материалов это приближение уже является достаточным.

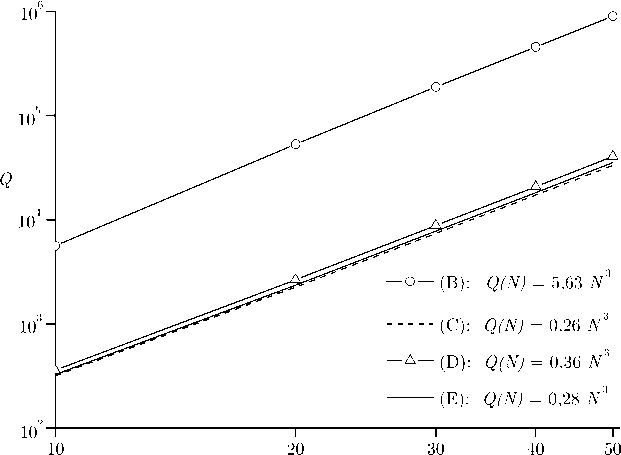
Рис. 1. Показатели добротности поперечной b -моды для цепочки частиц из GaAs в различных приближениях. Результаты для случая (F) n max = 4 не приведены, так как они отличаются от результатов в случае (E) менее чем на 1%

В этой статье мы предлагаем модель для оценки зависимости времени жизни τ моды (показатель добротности Q пропорционален времени жизни τ ) в линейной цепочке длины L = Na . Рассматриваем квантовую частицу единичной массы, движущуюся в потенциальном поле, которое равно U 0 >  0 в области — L < x < L и обращается в ноль вне этой области. Состояния этой частицы с энергией E , близкой к

U о ( \ E — U о | ^ E ), по свойствам аналогичны поляритонным модам в цепочке диэлектрических частиц, частоты которых лежат вблизи границы зоны. На основании этой модели в приложении показано, что показатель добротности моды с такой энергией возрастает при увеличении размера системы L по закону Q ~ L ³ , что эквивалентно формуле (5).

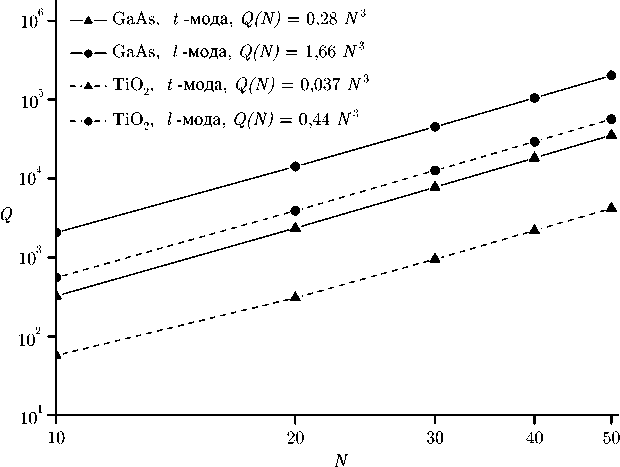
Рис. 2. Показатель добротности поперечной и продольной b -мод для цепочек частиц из GaAs и ТЮ 2 как функция числа частиц в цепочке, n max = 3

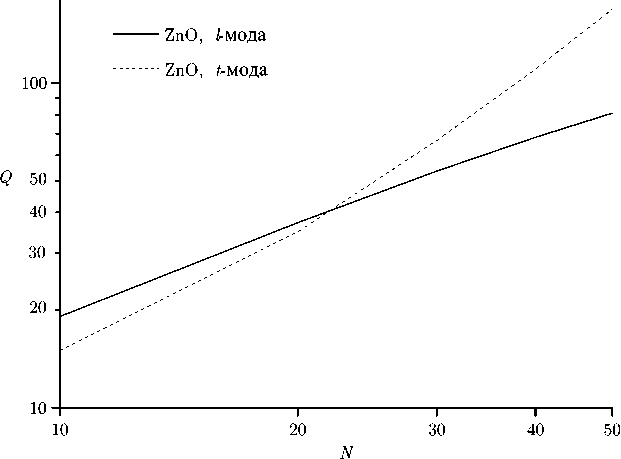
Рис. 3. Показатель добротности поперечной и продольной b-мод для цепочки частиц из ZnO как функция числа частиц, nmax = 2

Показатель добротности a-мод не обязательно растёт с ростом числа частиц по закону Q ∼ N3 , даже для проводящих мод. Вероятно, это связано с гибридизацией этих мод с быстро затухающими b-модами в том же интервале частот. Зависимость Q ∼ N3 показателя добротности наблюдается только для продольных a-мод в GaAs, что может быть связано с тем, что интервалы частот этих мод не перекрываются с частотными интервалами других мод. В любом случае, мы видим, что показатель добротности a-мод растёт с ростом числа частиц N медленнее, чем N3 , или что показатель добротности для этих мод меньше, чем для соот- ветствующих b-мод. Поэтому приведённый ниже анализ ограничивается b-модами для GaAs, TiO2 и ZnO. Показатели добротности для поперечных и продольных b-мод для этих материалов приведены на рис. 2, 3. Данные и графики были получены для nmax = 3 для GaAs и для nmax = 2 для TiO2 и ZnO, так как для этих материалов это приближение является достаточно точным.

Как для GaAs, так и для TiO ₂ продольные моды обладают более высоким показателем добротности. Показатели добротности продольных и поперечных мод в цепочках из TiO ₂ различаются в 4 раза, из GaAs — в 10 раз. Причина того, что время жизни продольных мод больше, чем поперечных, пока не ясна. Возможно, это связано с тем, что электромагнитные волны в вакууме поперечны, и поэтому интенсивность излучения электромагнитных волн поперечными модами выше, чем продольными.

Заметим, что этот результат отличается от результатов, полученных для кольцевых массивов частиц [7], для которых самым высоким показателем добротности обладает поперечная b -мода. Это объясняется тем, что в случае кольцевых массивов показатель добротности растёт с ростом числа частиц N экспоненциально Q ( N ) ~ exp( kN ), а множитель к тем больше, чем меньше частота моды. Поэтому в кольцевых массивах достаточно большого числа частиц низкочастотные моды всегда обладают самым высоким показателем добротности.

Поскольку поперечная b -мода в ZnO лежит совсем немного выше порога проводимости X/ 2 d = 1, а продольная мода лежит ниже его (см. табл. 1), для этих мод кубическая зависимость показателя добротности от числа частиц не наблюдается. Для малого числа частиц N <  22 продольные моды имеют более высокий показатель добротности, как и для GaAs и TiO ₂ . Однако для большего числа частиц показатель добротности поперечной моды оказывается больше, так как она, в отличие от продольной моды, является проводящей.

Стоит заметить, что моды, обладающие максимальным показателем добротности, обладают также максимальной групповой скоростью. Дело в том, что эти моды расположены вблизи верхней границы зоны проводимости, которой соответствует квазиволновой вектор, равный q = п/a. Частота как функция квазиволно-вого вектора ш (q) имеет экстремум в точке q = п/a [7, 9], поэтому групповая скорость вблизи верхней границы зоны обращается в ноль.

То обстоятельство, что максимальным показателем добротности (или наибольшим временем жизни) обладают моды с минимальной групповой скоростью, можно физически интерпретировать, основываясь на том, что радиационные потери в конечной цепочке происходят главным образом на концах цепочки. Это приводит к тому, что время жизни поляритонного возбуждения заданной частоты, имеющего вид волнового пакета конечных размеров, пропорционально времени распространения этого возбуждения вдоль цепочки. Следовательно, время жизни возбуждения тем больше, чем меньше групповая скорость при данной частоте.

Таким образом, цепочки диэлектрических частиц представляют собой реализацию «медленного света», описанного в статьях [14, 15], которые могут быть интересным дополнением к другим уже существующим реализациям [10–13].

• IV.    Заключение

В этой статье исследованы поляритонные возбуждения, формирующиеся в конечных линейных цепочках диэлектрических частиц, состоящих из GaAs (показатель преломления n r = 3 , 5), TiO ₂ (фаза рутила, n r = 2 , 7) и ZnO ( n r = 1 , 9). Рассматривались поперечные и продольные моды с максимальным временем жизни, то есть с максимальным показателем добротности. Частоты этих возбуждений отвечают первому резонансу Ми, связанному с коэффициентом b ₁ . Было показано, что частоты проводящих мод могут быть точно определены в самом простом приближении дипольного взаимодействия между частицами n max = 1, тогда как точная оценка показателя добротности получается в приближении n max = 3, что отвечает учёту одновременно дипольного, квадрупольного и октупольного взаимодействия между частицами.

Показано, что для материалов GaAs и TiO ₂ показатель добротности собственных мод возрастает с увеличением числа частиц в цепочке приблизительно по закону Q ~ N ³ . В отличие от кольцевых массивов частиц, в цепочках наибольшим показателем добротности обладает продольная мода. При этом групповая скорость мод, обладающих максимальным показателем добротности, стремится к нулю при увеличении длины цепочки. Зависимость Q ~ N ³ не наблюдается только для ZnO, обладающего наименьшим показателем преломления n r = 1 , 9, так как для этого материала моды с максимальным показателем добротности имеют частоту вблизи порога формирования проводящих мод.

V. Приложение

-С o V E — U о sin ( V E — UL^ =

= i V EC i e i^EL ,          (7)

где уравнение (6) записано для волновой функции, а уравнение (7) — для её производной. Делим уравнение (6) на (7), получаем

V E — U о tg ( V E — U о L )

i

. E

В нашем случае L ^ + то , E ^ U о , поэтому для того, чтобы левая часть равенства (8) оставалось конечной, необходимо, чтобы при достаточно больших L выполнялось условие

Здесь мы излагаем нашу физическую интерпретацию зависимости показателя добротности от длины цепочки на модели квантовой частицы, движущейся в потенциальном поле:

U о >  0 , - L < x < L, 0 , | x | > L,

V E — U о L = I — 5, 5 <  1 .    (9)

Из (8) следует, что

¹      • a         /77—77

---- = i—r=, a = E E ^— U о , tg aL E

U ⁽ x ) = {

а поскольку в силу (9)

tg aL =

Квазисостояние с минимальной энергией E>U 0 может быть использовано для оценки показателя добротности, как показано в уравнении (4). Массу квантовой частицы положим равной единице, так как это не влияет на зависимость показателя добротности от размера L . Тогда для x >  0 решение уравнения Шредингера можно представить в виде:

п/ 2 — aL¹

то, учитывая, что E ^ U о , а ~ п/ 2 L , по-

лучаем

— — aL 2

_г п и- ¹ / ^

i 2 LU ^о

Отсюда следует, что

Ф о ( x ) = C о cos ( V E — U 0 x) , x < L,

а = V E — U о =

п Л__ • ), 2 L V    L v U q У

Ф 1 ( x ) = c 1 e^{iV Ex} , x> L.

Как и должно быть для квазисостояний, на бесконечности волновая функция переходит в уходящую волну. В связи с симметрией модели достаточно наложить граничные условия в точке x = L , тогда граничные условия в точке x = — L будут выполняться автоматически. Граничные условия в точке x = L представляют собой требования непрерывности волновой функции и её производной: Ф _о ( L ) = Ф 1 ( L ), Ф 0 ( L ) = Ф 1 ( L ). Это приводит к следующей системе уравнений:

C о cos (V E — U о L ) = C 1 e^ L , (6)

откуда легко выразить значение энергии:

π ²        π ²

^E ~ U ^{о +} 4 L ² i 4 L з V U g .

Следовательно,

π ²                    π ²

^{3 E} = ^— H L v U O , ^{$ E} = ^U' + 4L2 “ ^U о ■

Тогда, по аналогии с формулой (4), показатель добротности может быть представлен в форме

_Q = _— S S = L 3 U 3 //

^Q 2 9 E   п ^{2 0} ,

что согласуется с результатом, полученным при исследовании показателя добротности цепочки частиц.