Оптические системы с многосекторными полями зрения на основе дифракционных элементов

ОПТИЧЕСКИЕ СИСТЕМЫ С МНОГОСЕКТОРНЫКИ ПОЛЯМИ ЗРЕНИЯ НА ОСНОВЕ ДИФРАКЦИОННЫХ ЭЛЕМЕНТОВ

При создании ряда устройств обработки информации, технического зрения и т.п. возникает необходимость построения оптических систем с многосекторными полями зрения. Такие системы должны обеспечивать пространственное совмещение изображений эквидистантных предметов, наблюдаемых под различными углами. С функциональной точки зрения системы с многосекторными полями состоят из двух основных компонентов: демультипликатора, осуществляющего совмещение пучков, распространяющихся под различными углами, и объектива, формирующего изображение.

Наиболее простым по конструкции демультипликатором является дифракционная решетка, формирующая в различных дифракционных порядках пучки одинаковой интенсивности [1]. Если при этом в качестве объектива используется одиночная дифракционная линза, то вся система в целом может быть изготовлена в виде одной оптической детали - плоскопараллельной пластины, на противоположных гранях которой выполнены линейная и кольцевая рельефно-фазовые дифракционные структуры. Работа такой пластины в каждом порядке дифракционной решетки, за исключением нулевого, эквивалентна работе внеосевого голограммного оптического элемента (ГОЗ).

Фокусирующие и аберрационные свойства внеосевого ГОЭ, формирующего изображение на сферической поверхности, рассмотрены в работе [21. Учитывая, что приемники излучения, как правило, рассчитаны на сопряжение с оптическими системами, формирующими плоское изображение, в настоящей работе рассматриваются фокусирующие и аберрационные свойства внеосевого ГОЭ при формировании изображения на плоскости, нормальной к оси наблюдения.

Наиболее общая голографическая схема получения внеосевого ГОЭ, предназначенного для формирования изображения достаточно удаленных объектов, представлена на рис, 1. На длине волны записи Ао ГОЭ будет формировать безаберрационное изображение бесконечно удаленного точечного источника, расположенного на прямой 0-,0. Эту прямую, являющуюся осью коллимированного пучка записи, в дальнейшем будем называть осью диаграммы направленности ГОЭ на длине волны Ао - Ось 00’, в точке О* которой будет формироваться безаберрационное изображение, назовем осью наблюдения, саму точку О' - фокусом ГОЭ, а расстояние 00' = f^ - фокусным расстоянием элемента.

Если бесконечно удаленный точечный источник не находится на оси диаграммы направленности или длина волны его излучения А не совпадает с Ао, то изображение источника смещается из точки О' и искажается абер-

Рис. 1. Голографическая схема получения внеосевого ГОЭ:

1, 2 - коллимированный и сходящийся пучки записи;

3 - плоскость записи рациями. Для определения параксиальных координат изображения и оценки аберраций в этом случае необходима формулы расчета хода лучей через внеосевой ГОЭ. Такие формулы могут быть получены с использованием аппарата, изложенного в работе [3].

В системе координат XYZ, в которой начало координат совпадает с центром апертуры ГОЭ, плоскость YOZ проходит через оси диаграммы направленности и наблюдения, а ось 0Z нормальна к плоскости ГОЭ (рис. 2), формулы, связывающие направляющие косинусы падающего (m^, m , т^) и дифрагированного (т1 , т', тТ) лучей имеют вид х У z

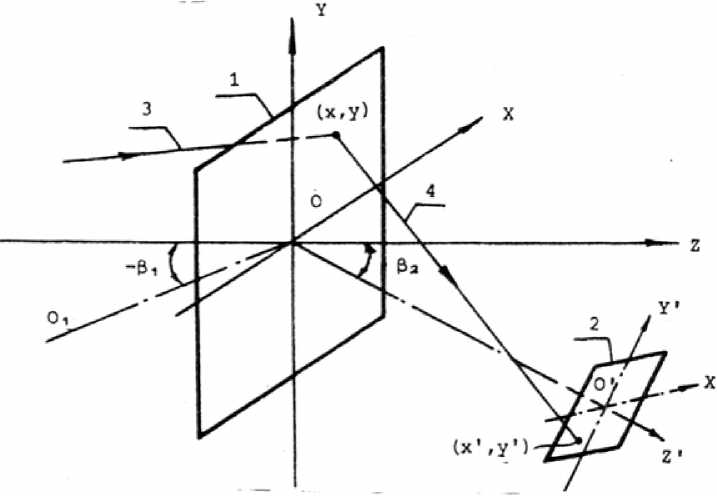
Рис. 2. К расчету хода лучей через внеосевой ГОЭ:

1 - плоскость дифракционной структуры ГОЭ;

2 - фокальная плоскость элемента;3, 4 -падающий и дифрагированный лучи

m* = mx - ЦЙх;'

my = my " pfsin ed + fi(y - f* sin Уд)]; I(1)

m* = /1 - m’2 ~ m|2 ,I zx у где

Q = L_ f ! + x2 + y= _ 2y sin P3 )4, fo         ^2        fo(2)

U = X/Xq*

Формулы (1) получены в предположении, что ГОЭ работает в минус пер вом порядке дифракции и находится в воздухе. Координаты точки пересечения дифрагированного луча с фокальной плоскостью (плоскостью, нормальной к оси наблюдения и отстоящей на рас стоянии fy ст центра апертуры ГОЭ) в системе координат X'Y’Z', связанной с этой плоскостью и осью наблюдения (см, рис, 2) , имеют вид х ' = х + Gm';1

х                              \(3)

у* = у + G{m' cos Ра - in1 Sin Эд)| где fo - у sin Эд G = ——----------------------*(4)

m^ sin Э_а + m^ cos Э_а

Обозначим через Е(Е') тангенс угла между падающим (дифрагированным) лучом и плоскостью YOZ, то есть меридиональной плоскостью; через п(п’) тангенс угла между падающим (дифрагированным) лучом и осью диаграммы направленности ГОЭ (осью наблюдения), измеренный в меридиональной плос' кости. Параксиальные формулы и формулы для аберрационных коэффициентов можно получить, разложив выражения (1) — (4) в ряды по степеням х, у, Е, И и ограничив их членами требуемого порядка малости. В параксиальном приближении ряды ограничиваются членами первого порядка и из (1)-(4) получаем

х* = f;g + м^;ох .                   хр- , „хр*

у' = fQn + м0001п + моооо + мо100у, где хр.

^ооо мхр*

ОО о мхр'

О 1 о о

Mq о О 1

дл.

, /дх^ / sin &1 - Sin е_а

°       \ COS $а

( " |cos Ра;

I Ао /               \

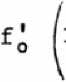
cos От ] cos Эд/ *

Первые три коэффициента выражений (6) определяют хроматизм внеосе-хр.                                                               хр, вого ГОЭ: М q00 - сагиттальный хроматизм первого порядка, Моооо и хр. М0100 ~ меридианальный хроматизм соответственно нулевого и первого порядков. Коэффициент М0о01 характеризует анаморфотность внеосевого ГОЭ.

Переходя к определению первичных монохроматических аберраций, от метим, что у оптических систем, не имеющих оси симметрии, первичными являются аберрации второго порядка. Полагая в формулах (1) ц = 1, раз лагая (1>—(4) в степенные ряды и ограничиваясь членами второго порядка малости относительно величин х, у, £ и п, получим для внеосевого ГОЭ следующие выражения первичных монохроматических аберраций:

Ах^ — МО110у£;                                          (

ДУа — ^Ю1ОХ^ + ^ОЛОтУГ + ^‘0020^  "*" ^0002*1

где мО1,о = -sin Sa?

^1 о 1 о ~ —^9 Sa;

Иою-г = -2COS ^ tg 0а;

^оо2о ~ Т ^° ^9 S3;

1   , /cos3 sin ~ sin Pt cos2 82

M     = ±           .--------—----------—

0002   2 °\           cos3 8a

В соответствии с работой [4] дадим следующие названия полученных аберрационных коэффициентов:

М , М им - коэффициенты астигматизма; O11O1O1O О 1 О 1

МОоОЗ И моо2о ~ соответственно коэффициенты масштабной и параболической дисторсии.

Приведенные здесь выражения могут быть положены в основу расчета и анализа оптических систем, включающих внеосевые ГОЭ, и в частности ди фракционных систем с многосекторными полями зрения.