Оптический дифференциатор на основе трехслойной металлодиэлектрической структуры

В последние годы наблюдается всплеск интереса к разработке компактных структур фотоники для дифференцирования оптических сигналов, а также для реализации более сложных дифференциальных операторов. Указанные дифференцирующие структуры рассматриваются в качестве перспективной элементной базы для новых электронно-оптических устройств обработки информации [1, 2].

В рамках линейной оптики преобразование оптического сигнала, происходящее при его взаимодействии с дифракционной структурой, может быть описано в рамках теории линейных систем [3–6]. Передаточная функция (ПФ) дифракционной структуры пропорциональна коэффициенту отражения (пропускания) структуры, рассматриваемому как функция пространственной частоты (тангенциальной компоненты волнового вектора падающей волны) или угловой частоты. Поскольку ПФ идеального дифференцирующего фильтра обращается в нуль на центральной частоте, то необходимым условием для оптического выполнения операции дифференцирования является наличие нуля в спектре отражения (пропускания) дифракционной структуры. Нули в спектре отражения (пропускания), как правило, обусловлены резонансными эффектами возбуждения собственных мод структуры. В этой связи для оптической реализации операций дифференцирования были предложены различные резонансные структуры, включающие брэгговские решётки с «дефектом» периода [5–9], трехслойные структуры с «W-образным» профилем показателя преломления (т.н. W-структуры) [10], плазмонные структуры на основе схемы Кречмана [11, 12], дифракционные решётки [3, 13– 16].

Кроме того, теоретически было показано, что достижение строгого нуля в спектрах отражения границы раздела диэлектрических сред на основе эффекта Брюстера может быть использовано для пространственного дифференцирования поляризованных оптических сигналов [17, 18]. Экспериментальные и теоретические исследования, проведённые для случая отражения ТМ-поляризованного света от грани стеклянной призмы под углом Брюстера, показали высокую эффективность такого подхода для выполнения аналоговой операции выделения контуров изображений амплитудных и фазовых объектов [19–21]. Основным преимуществом реализации оптического дифференциатора на основе границы раздела сред диэлектрик-диэлектрик является очевидная простота изготовления. Преобразование оптического сигнала, определяемое коэффициентом отражения структуры, хорошо аппроксимируется ПФ дифференциатора первого порядка для углов падения вблизи угла Брюстера. При этом максимальная амплитуда коэффициента отражения в этой области имеет порядок 10 –3.

Таким образом, недостатком этого подхода является необходимость повышения интенсивности падающего пучка на несколько порядков для надёжной регистрации отраженного изображения.

Помимо резонансных структур, для выполнения операции дифференцирования по пространственной переменной были предложены компактные аналоги коррелятора с градиентными линзами, в которых пространственный фильтр представлен метаповерхностью, кодирующей функцию комплексного пропускания дифференцирующего фильтра [1, 22–24]. По мнению авторов настоящей статьи, дифференциаторы на основе резонансных структур (систем слоев и дифракционных решеток) значительно компактнее, поскольку не требуют дополнительных линз, выполняющих преобразование Фурье. Кроме того, резонансные структуры существенно более просты в изготовлении по сравнению с метаповерхностями, которые обычно представляют собой массив нанорезонаторов.

В настоящей статье впервые исследовано выполнение операций дифференцирования по пространственной координате и во времени с помощью простой структуры металл–диэлектрик–металл (МДМ), работающей на отражение. Указанная МДМ-структура состоит из верхнего металлического слоя, диэлектрического слоя и металлической подложки. Структуры такого типа широко используются в качестве абсорберов света [25–30]. Эффект поглощения света в МДМ-структуре имеет резонансную природу и обусловлен возбуждением мод структуры, локализованных в диэлектрическом слое. Важно отметить, что несмотря на то, что представленные в известных работах [25–30] результаты численного моделирования и экспериментального исследования МДМ-структур показывают наличие в спектрах отражения зон с близким к нулю отражением, в указанных работах не представлено теоретического обоснования того, что коэффициент отражения МДМ-структуры может строго обращаться в нуль. В настоящей работе приведено строгое доказательство этого факта. Из представленного доказательства следует, что при заданных материалах, длине волны и угле падения излучения всегда можно получить нулевое отражение за счет выбора толщин металлического и диэлектрического слоев МДМ-структуры. По мнению авторов настоящей работы, этот результат является важным и, в частности, обосновывает возможность использования МДМ-структуры для дифференцирования оптических сигналов. Представленные в работе результаты численного моделирования показывают, что МДМ-структура позволяет с высоким качеством реализовать вычисление первой производной по пространственной переменной и во времени.

1.    Исследование оптических свойств структуры металл–диэлектрик–металл

Исследуемая в данной статье МДМ-структура схематически изображена на рис. 1. Данная структура состоит из верхнего металлического слоя (толщина hm, диэлектрическая проницаемость εm), диэлектрического слоя (толщина hd, диэлектрическая проницаемость εd) и металлической подложки (диэлектрическая проницаемость εm). Для простоты будем считать, что материал над структурой соответствует вакууму (диэлектрическая проницаемость ε = 1).

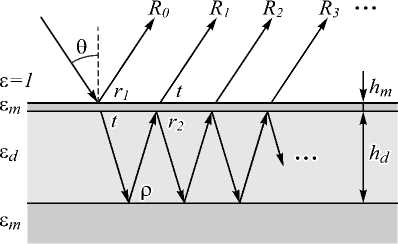
Рис. 1. Геометрия структуры металл–диэлектрик–металл и модель многолучевой интерференции

Получим коэффициент отражения структуры для случая падения плоской волны. Будем считать, что падающая волна имеет единичную амплитуду и некоторую фиксированную поляризацию (ТЕ- или ТМ). Обозначим k x = k 0 sin θ тангенциальную компоненту волнового вектора падающей волны, где θ – угол падения, k 0 =2 π / λ – волновое число, λ – длина волны. Для получения коэффициента отражения воспользуемся моделью многолучевой интерференции [31]. В рамках этой модели отраженная от МДМ-структуры плоская волна представляется в виде суммы плоских волн, отраженных различное число раз от металлической подложки (рис. 1). Обозначим R m , m =0, 1, 2,... амплитуды отраженных волн, где индекс m описывает число отражений от металлической подложки. Волна с индексом m =0 соответствует волне, отраженной от верхнего металлического слоя, расположенного между двух однородных полубесконечных диэлектрических сред, и имеет амплитуду R 0 = r 1 , где r 1 – комплексный коэффициент отражения металлического слоя. Амплитуду отраженной волны R m , испытавшей m ≥ 1 отражений от подложки, несложно получить в виде:

R m = t ² ρ ^mr 2 ^{m - 1} e ^{2 imkzhd} ,                                       (1)

где t и r 2 – коэффициенты пропускания и отражения металлического слоя, расположенного между двух однородных полубесконечных диэлектрических сред, для плоской волны, падающей со стороны диэлектрического слоя, ρ – коэф фициент отражения металлической подложки, k z = k 02 ε d - k x 2 – z -компонента волнового вектора отраженной от подложки плоской волны в диэлектрическом слое. Несложно заметить, что коэффициенты R m образуют геометрическую прогрессию со знаменателем q = r 2 ρ ⋅ e 2 i k zh d . С учетом этого факта коэффициент отражения МДМ-структуры можно получить в виде:

”         I'W kz*

R = V Rm = r . pte---- m=0            1- r2pe2,kzhd r - e 2ikzhd p(r1 r — 12)

1 - r ₂ p e ² ik z h d

. (2)

Отметим, что коэффициенты r 1 , r 2 , t в (2) зависят от параметров падающей волны (длины волны, угла падения, поляризации) и рассчитываются по известным формулам [31], описывающим отражение и пропускание плоской волны при прохождении через плоскопараллельный слой однородного материала (в данном случае – из металла с диэлектрической проницаемостью e _m ). Коэффициент отражения подложки p определяется по формулам Френеля. Выражение (2) является строгим и может быть также получено в рамках формализма матрицы рассеяния [32, 33] или с использованием модели связанных волн [34].

Отметим, что рассматриваемая МДМ-структура является резонансной, поскольку в ней могут существовать вытекающие моды, локализованные в диэлектрическом слое. Дисперсионное уравнение мод получается приравниванием к нулю знаменателя выражения (2):

• 1    - r ₂ p e ^{2 ikzhd} = 0. (3)

Из уравнения (3) могут быть рассчитаны комплексные константы распространения (или комплексные длины волн) собственных мод МДМ-структуры, соответствующие полюсам коэффициента отражения, рассматриваемого как функция от k x (или от длины волны). В ряде случаев в резонансных структурах коэффициент отражения может обращаться в нуль [11, 30]. Данное свойство является важным с практической точки зрения и, в частности, позволяет использовать резонансную структуру для оптического дифференцирования.

Используя полученное представление коэффициента отражения (2), покажем, что при определенном выборе параметров h m и h d коэффициент отражения рассматриваемой МДМ-структуры обращается в нуль. Согласно (2), коэффициент отражения обращается в нуль при выполнении условия

----¹— = e ² ik z h d p , r r - 1 ²

Выражение (4) связывает комплексные величины и поэтому эквивалентно равенству модулей и аргументов левой и правой частей:

r 1

Г 1 r - 11

= lpl,

,         1 If         Г 1          1,4

h d =--- arg I-----------I + 2 n n

2 k z I     (p ( r Г 2 - 1 ² ) )

n G N .

Покажем, что соотношение (5) всегда может быть выполнено за счет выбора толщины hm верхнего металлического слоя, от которой зависит только левая часть (5). Рассмотрим, как меняется левая часть выражения (5) при изменении hm. При hm ^ 0 коэффициен- ты r1, r2, t стремятся к коэффициентам отражения и пропускания f, r2, t для плоской границы раздела между вакуумом и диэлектриком с диэлектрической проницаемостью ed. Заметим, что выражение r r2 - f2 в (5) является определителем матрицы рассеяния для плоской границы раздела между вакуумом и диэлектриком [34]. В силу унитарности данной матрицы |rr2 -121 = 1, и, следовательно, левая часть (5) стремится к величине |f| при hm ^ 0. При hm ^ да, t ^ 0 и левая часть (5) стремится к величине 1/|r2| > 1. Таким образом, при увеличении толщины металлического слоя hm левая часть (5) непрерывно изменяется от величины |/11 < 1 до величины 1/|r2|>1. Величина |p|, стоящая в правой части (5), меньше единицы. Кроме того, для большинства металлов можно считать, что Ip| > |П|, и поэтому существует значение hm, при котором равенство (5) выполняется. Расчет значения hd при известной толщине hm металлического слоя, обеспечивающей выполнение равенства (5), осуществляется по формуле (6).

В качестве примера на рис. 2 показаны толщины металлического и диэлектрического слоев МДМ-структуры, рассчитанные из условий нулевого отражения (5), (6), при различных угла падения 9 и для различных металлов (золота, серебра, алюминия). Расчет производился для случая падающей волны с TE-поляризацией при длине волны X = 630 нм. В качестве диэлектрической проницаемости диэлектрического слоя использовалось значение ε d = 2,25. Для выбранной длины волны диэлектрические проницаемости металлов ε m равны – 18,096 + 0,48422i (серебро), – 11,548 + 1,2821i (золото), – 54,325 + 21,478i (алюминий) [35]. Толщина металлического слоя h m для каждого угла падения определялась из решения уравнения (5). Для решения данного уравнения использовался т.н. метод доверительной области (англ. trustregion method), реализованный в функции fsolve в пакете MATLAB. Расчет значений h d осуществляется по формуле (6) при n =0 на основе полученных значений h m . В этом случае, как видно из рис. 2, общая толщина ( h m + h d ) МДМ-структур, обладающих нулевым отражением, не превышает 270 нм.

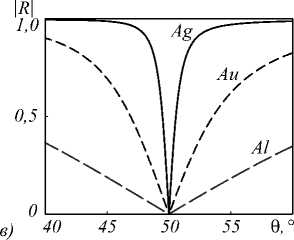
В качестве примера на рис. 3 показаны угловые спектры отражения |R(9)| МДМ-структур, имеющих нуль коэффициента отражения при углах падения 9 = 0 (рис. 3а) 9 = 30° (рис. 3б) и 9 = 50° (рис. 3в). Параметры структур (толщины металлического и диэлектрического слоев) отмечены точками на графиках на рис. 2. Для проверки правильности расчетов спектры на рис. 3 были рассчитаны не по формуле (2), а на основе строгого решения уравнений Максвелла методом [36]. Графики спектров подтверждают наличие нулевого отражения при заданных углах падения. Отметим, что в окрестности нормального падения (рис. 3а) коэффициент отражения является четной функцией угла падения и поэтому имеет нуль второго порядка [6]. Из рис. 3 видно, что ширина минимумов отражения зависит от выбранного металла и от угла падения. Наименьшая ширина минимумов отражения достигается для серебра, обладающего наибольшей отражательной способностью. Кроме того, ширина минимумов отражения при 9 = 30° больше ширины минимумов при 9 = 50°. Это связано с увеличением добротности резонансов с ростом угла падения.

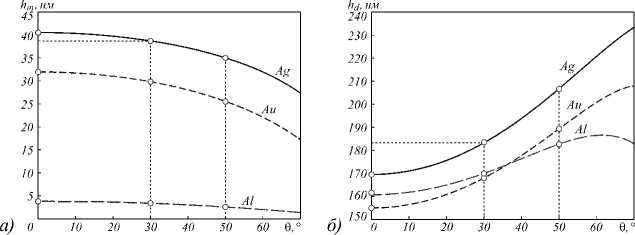
Рис. 2. Толщины верхнего металлического слоя (а) и диэлектрического слоя (б) МДМ-структуры в зависимости от угла падения, обеспечивающие нулевое отражение. Точками отмечены значения толщин слоёв при углах падения 0°, 30° и 50°, использованные при расчёте спектров на рис. 3

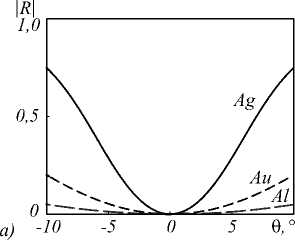
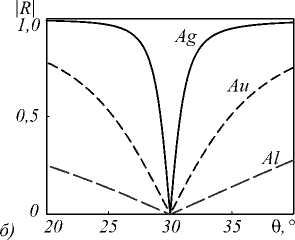
Рис. 3. Угловые спектры отражения \R.( 0 )\ для МДМ-структур из различных металлов, рассчитанных из условия нулевого отражения при углах падения 9 = 0° (а), 9 = 30° (б) и 9 = 50° (в)

направлением плоской волны и осью z inc . Будем считать, что пространственный спектр пучка G ( k x ,inc ), | k x , _inc | 5 g , описывающий амплитуды составляющих пучок плоских волн, является достаточно узким ( g << k 0 n sup ), так что k_{z м} = ^ k 02 n _s ² up - k^ nc ® k 0 n sup . В этом случае падающий пучок имеет следующий вид:

u inc ( x inc , z inc ) exp ( i^k 0 z inc ) J G ( ^k x ,inc ) ^X X exp ( ik x ,inc x inc ) d k x ,inc ^.

Легко видеть, что преобразование спектра падающего пучка G ( k x ,inc ), происходящее при отражении от структуры, описывается умножением на коэффициент отражения R ( k x ), рассматриваемый как функция x -компоненты волнового вектора плоской волны, падающей под углом у + 9 ₀:

k x = k 0 n sup sin ( y + 9 0 ) ® k x ,inc cos 9 0 + k x ,0 , (9)

u inc

x inc ,

z inc ) exp ⁽ ik 0 z inc ) P nc ⁽ x inc ) ,

где P inc ( x inc ) – поперечный профиль пучка, а функция u ( x inc , z inc ) соответствует y -компоненте электрического или магнитного поля в зависимости от поляризации (ТЕ или ТМ соответственно). Падающий пучок может быть представлен в виде суперпозиции плоских волн с различными значениями пространственной частоты k x ,_mc = k ₀ n _sup sin у , где у - угол между

где k x ,0 = k 0 sin 9 0 . При этом профиль отраженного пучка в системе координат отраженного пучка ( x refl , z refl ) (рис. 4) принимает вид

P refl ( x refl ) = J G ( k x ,inc ) R ( k x ) X X exp ( ik x ,inc x refl ) d k x ,inc ^.

Согласно (8– 10), преобразование профиля пучка при отражении P _inc ( x _inc) ^ P refl ( x _refl) можно описывать

как преобразование сигнала P inc ( x inc ) линейной системой со следующей ПФ [5, 10]:

H s ( k x ,inc ) = R ( k x ,inc cos θ 0 + k x ,0 ) .                   (11)

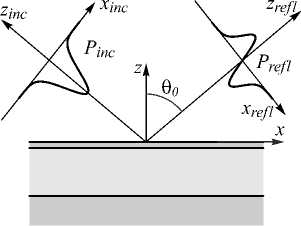
Рис. 4. Геометрия задачи дифракции пучка на МДМ-структуре и схематичное изображение операции пространственного дифференцирования

Аналогично можно показать, что для импульса, соответствующего суперпозиции плоских волн с фиксированным направлением, но с различными частотами ω = ω inc + ω 0 , где ω 0 – центральная частота, преобразование формы огибающей импульса, происходящее при отражении от структуры, описывается выражением [3, 4]

P refl ( t ) = ∫ G ( ω inc ) R ( ω ) exp ( - i ω inc t ) d ω inc , (12)

где G ( ω inc ), | ω inc | ≤ Ω – спектр огибающей падающего импульса, R ( ω ) – коэффициент отражения структуры, рассматриваемый как функция частоты. Легко видеть, что ПФ линейной системы, описывающей преобразование (12), имеет вид [3, 4]

H t ( ω inc ) = R ( ω inc +ω 0 ) . (13)

Как показано в предыдущем параграфе, параметры МДМ-структур (толщины металлического и диэлектрического слоев) могут быть выбраны из условия нулевого отражения при заданном угле падения θ = θ 0 и частоте ω = ω 0 (или длине волны λ = λ 0 =2 π c / ω 0 ). В этом случае, разлагая ПФ (11) и (13) в ряды Тейлора в окрестности точек k x ,inc =0 и ω = ω 0 до линейных членов, получим:

H s ( k x ,inc ) ^{≈ α} s k x ,inc , H t (^ω inc ) ^{≈ α} ω k x ,inc . (14)

Передаточные функции (14) пропорциональны ПФ дифференциатора по пространственной переменной Hdiff (kx,inc) = ikx,inc и ПФ дифференциатора во времени Ht,diff (ωinc) =– iωinc соответственно. Таким образом, представленный теоретический анализ показывает возможность использования МДМ-структуры в качестве оптического дифференциатора. Отметим, что добротность резонанса (ширина резонансного минимума) для рассматриваемой структуры определяется как углом падения, так и выбранным металлом (см. рис. 3). Поэтому за счет выбора угла падения и / или металла можно получить требуемый интервал линейности для ПФ (14), согласованный с шириной пространственного или частотного спектра падающего пучка. Выполнение операции дифференцирования профиля пучка по пространственной переменной схематично показано на рис. 4.

Отметим, что представление (14) для H s ( k x ,inc ) верно только при наклонном падении (при θ 0 ≠ 0), поскольку в окрестности нормального падения коэффициент отражения является четной функцией от k x (см. рис. 3 а ). Представление для H t ( ω inc ) остается верным и при нормальном падении.

3.    Результаты численного моделирования МДМ-дифференциаторов

Рассмотрим возможность использования рассмотренной МДМ-структуры для выполнения операций дифференцирования по пространственной переменной и во времени. Операцию пространственного дифференцирования рассмотрим на примере ТЕ-поляризованного монохроматического падающего пучка с Гауссовым профилем P inc ( x inc ) = exp( - x _i²_nc / σ ² x ), σ x =8 мкм и длиной волны λ 0 =630 нм (частотой ω 0 = 2,9899 ⋅ 10 15 c –1 ). Операцию дифференцирования во времени рассмотрим для ТЕ-поляризованного импульса с Гауссовым профилем огибающей P inc ( t ) = exp( - t 2 / σ t 2 ), σ t =88 фс и центральной частотой ω 0 = 2,9899 ⋅ 10 15 c –1 .

На рис. 5 показаны пространственная и временная ПФ МДМ-структур при угле падения θ =30 ° и при использовании золота в качестве металла. Соответствующие толщины металлического и диэлектрического слоев МДМ-структуры отмечены точками на соответствующих золоту графиках на рис. 2. Точечными линиями на рис. 5 показаны нормированные спектры профиля падающего пучка G ( k x , inc ) ∝ exp( - k x 2, inc σ 2 x /4) и огибающей импульса G ( ω inc ) ∝ exp( -ω i2nc σ t 2 /4) . Вертикальными точечными линиями отмечены ширины спектров по уровню 1 /e².

Из рис. 5 видно, что спектры профиля падающего пучка и огибающей падающего импульса по большей части лежат в интервалах линейности ПФ. В этой связи следует ожидать хорошего качества дифференцирования. Отметим, что линейная фаза в ПФ (рис. 5) описывает лишь сдвиг (задержку) отраженного пучка (импульса) и не влияет на качество дифференцирования.

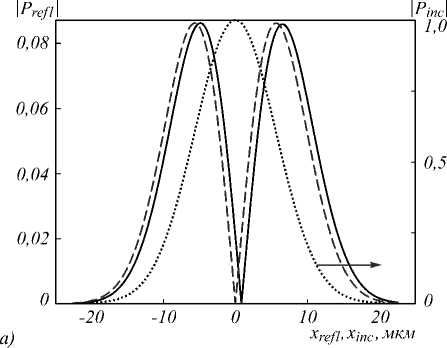
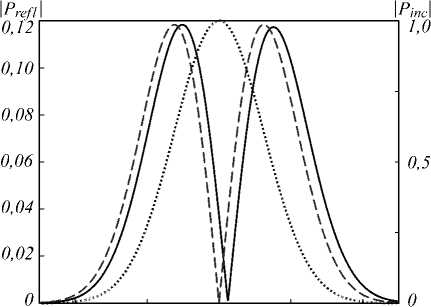
На рис. 6 показаны профиль отраженного пучка Prefl (xrefl) , рассчитанный по формуле (10), и огибающая отраженного импульса, рассчитанная по формуле (12), которые формируются при ПФ, показанных на рис. 5. Для сравнения пунктирными линиями показаны модули аналитически вычисленной производной по пространственной переменной от профиля падающего пучка (рис. 6а) и аналитической производной по времени от огибающей падающего импульса (рис. 6б). Модули производных приведены с масштабными множителями, выбранными из условия совпадения максимумов аналитических производных и отраженных сигналов. Рис. 6 показывает высокое качество дифференцирования. В случае дифференци- рования по пространственной переменной (рис. 6а) среднеквадратическое отклонение (СКО) модуля профиля отраженного пучка от аналитической производной, нормированное на максимальную амплитуду отраженного пучка, составляет 0,6%, а в случае дифференцирования по времени – 1,1 %. Отметим, что при расчёте нормированных СКО сдвиг (задержка) отраженного пучка (импульса) не учитывался.

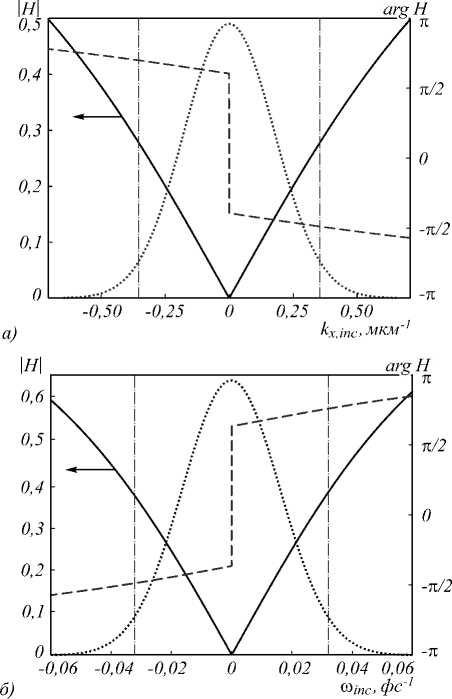
Рис. 5. Модули (сплошные линии, шкала слева) и фазы (штриховые линии, шкала справа) пространственной ПФ (а) и временной ПФ (б) МДМ-структуры при угле падения θ = 30° и материале металлических слоев золото. Точечными линиями показаны нормированные спектры профиля падающего пучка и огибающей импульса. Вертикальными штрихпунктирными линиями отмечены ширины спектров по уровню 1/e²

По мнению авторов настоящей работы, рассмотренная МДМ-структура имеет ряд практических преимуществ перед дифференциаторами на основе брэгговской решётки с «дефектом» периода [5, 6], W-структуры [10], а также «плазмонным» дифференциатором на основе схемы Кречмана [11]. Для брэгговской решётки с «дефектом» периода (а также для диэлектрической дифракционной решетки и произвольной системы диэлектрических слоев) условие нулевого отражения может строго выполняться только при наличии у структуры горизонтальной плоскости симметрии [15]. Условие наличия горизонтальной симметрии является неудобным при практической реализации дифференциатора, когда оптический пучок падает из воздуха, а сама структура располагается на некоторой диэлектрической подложке. В этом случае для получения нулевого отражения необходимо вводить пучок через призму, имеющую показатель преломления, равный показателю преломления подложки. Это существенно увеличивает габариты дифференциатора. Такой же недостаток (наличие призмы) имеют дифференциатор на основе W-структуры и плазмонный дифференциатор на основе схемы Кречмана.

-200    -100     0      100     200

б)                                                t. фс

Рис. 6. Модули профилей отраженных сигналов (сплошные линии, шкала слева) и аналитически рассчитанных производных (штриховые линии, шкала слева) при монохроматическом падающем пучке (а) и временном импульсе (б). Точечными линиями показаны профили падающего пучка и огибающей падающего импульса (шкала справа)

Заключение

В рамках модели многолучевой интерференции получено выражение для коэффициента отражения МДМ-структуры, состоящей из верхнего металлического слоя, диэлектрического слоя и металлической подложки. С использованием полученного выражения доказано, что коэффициент отражения МДМ-структуры может строго обращаться в нуль. Из приведенного доказательства следует, что при заданных материалах, длине волны и угле падения излучения нулевое отражение всегда можно получить за счет выбора толщин ме- таллического и диэлектрического слоев МДМ-струк-туры. Наличие нуля отражения позволяет использовать МДМ-структуру в качестве оптического дифференциатора. Приведенные результаты численного моделирования демонстрируют возможность оптического вычисления производной по пространственной координате и во времени. Аналогично [10], помимо выполнения операций пространственного дифференцирования и во времени, МДМ-структура может быть использована для одновременного дифференцирования во времени и по пространственной переменной. Полученные результаты могут найти применение при создании систем аналоговых оптических вычислений и оптической обработки информации.

Работа выполнена при поддержке гранта Российского научного фонда (проект № 19-19-00514) в части исследования оптических свойств МДМ-структуры (параграфы 1, 2), Российского фонда фундаментальных исследований (проект 18-07-00613) в части исследования МДМ-дифференциаторов (параграф 3) и Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристалло-графия и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) в части создания программных средств для моделирования работы дифференцирующих МДМ-структур (параграф 3).