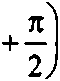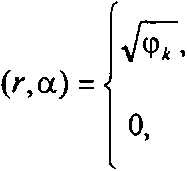Оптический метод структурирования контурных изображений

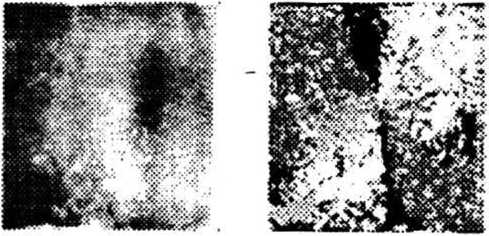
Специфический характер и сложность анализа таких объектов, как отпечатки пальцев, интерферограммы, кристаллограммы [1,2], и других контурных изображений, требует предварительной обработки таких изображений с целью выделения наиболее важной информации из массы несущественных деталей. Для этого предлагается структурировать контурное изображение [1] путем построения поля направлений, характеризующего направление линий в каждой точке изображения. Это приводит к сжатию информации, так как целый набор линий заменяется на их направление, а также к выделению особых точек контурного изображения.

В [3] разработано и исследовано несколько цифровых методов построения и обработки поля направлений. Однако, часто из соображений быстродействия или как дополнение к готовой оптической системе [4,5] желательно оптическое структурирование поступающего на вход изображения. В данной работе рассматривается оптикоэлектронный метод построения поля направлений с помощью вращающейся щели и амплитудной маски, установленных в частотной плоскости.

С целью исследования работоспособности предлагаемого метода средствами компьютерного моделирования проведено сравнение его с цифровым дисперсионным методом [3] для различных модельных и натурных изображений. Показана работоспособность и эффективность разработанного метода в численных экспериментах по распознаванию отпечатков пальцев с помощью оптического разложения Карунена-Лоэва [4,5].

• 1,    Оптический метод построения поля направлений,

Полем направлений [1] называется функция ф(х$у), значение которой в данной точке равно углу касательной к линии равного уровня функции w(x,y) в этой же точке, приведенному к диапазону [0е, 180е):

( дМдх\                    m

Ф(х,^) = arctg                                       (1)

• V oXicyj

где A(x,y)=w(x,y)-coiist=0 - линия уровня (см. Рис.1).

Рис.1. Определение угла наклона касательной к линии равного уровня изображения при построении поля направлений.

Понимание оптического метода построения поля направлений основано на представлении контурного изображения w(x,y), например, интерферограммы, в виде набора косинусных дифракционных решеток, ограниченных некоторыми областями, с различными углами наклона и частотой штрихов:

N

*(х,у) = £й(х,у)со8(а,х + Р,у)                      (2)

г=1

где q_t (х,у) - функция области, ограничивающей /-ю решетку; cos(a/ х+0у у) - /-ая решетка с параметрами а/ и ру , определяющими частоту и наклон штрихов.

И, Селекция направлений.

Угол наклона штрихов (р определяется через параметры решетки аир следующим образом:

^ = ^^ф        a_

<                 => tg ф = (3)

ax + Ру = constр

Представим:

cos(ax + Ру) = 1{ехр[/(ах + Ру)] + ехр[-/(ах + Ру)]}.

Тогда преобразование Фурье от функции решетки:

cos(ax + ру) —^ ^ {§(£ - а, л - Р) + 5(^ + а, т] + р)}(4)

где (х,у) и (^/q) - декартовы координаты во входной и частотной плоскостях, 3 -двумерное преобразование Фурье, 8(х,у) - функция Дирака.

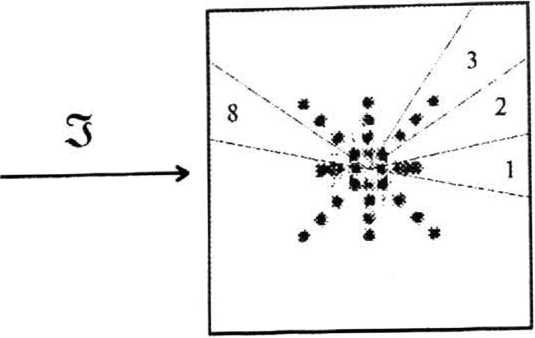
Таким образом, решетка дает в Фурье-плоскости два 8-импулъса, расположенные симметрично на линии, проходящей через центр (см. рис.2) под углом 6:

tgO = —

a

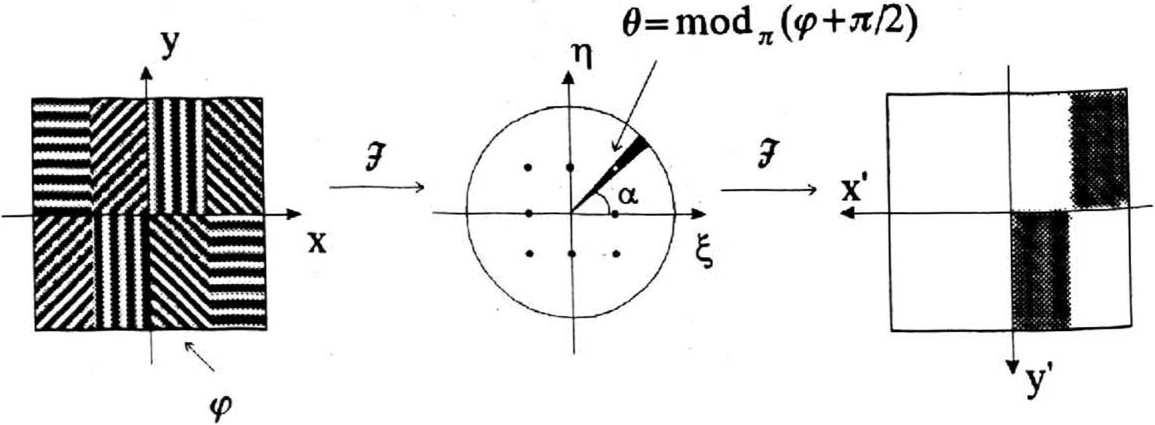
Рис. 2. Селекция направлений с помощью оптического метода с вращающейся щелью.

Тогда 6 и <р с учетом (3) связаны следующим образом:

tgO = --— = -ctgcp = td ф+-                     (5)

tg(p                   2У т.е., О перпендикулярен углу наклона штрихов решетки ф.

Если решетка ограничена некоторой областью ^(х,у), то в частотной плоскости мы получим свертку Фурье-образа от функции, описывающей эту область, £(£,п) с 8-импульсами. Так, при сканировании изображения прямоугольными окнами функция области ^(x,y)=rect(x,y), а ее Фурье-образ O(^,Ti)=sinc(§,Ti).

Известно, что свертка 8-функции с любой функцией дает ту же функцию с соответствующим смещением:

ОД - £о>п - По) ® №, п) = 2(£ - 5о> п- По)                (6)

Тогда, в описанном выше примере, мы получим вместо 8-импульсов расположенные точно также sinc-функции.

Далее, если с помощью щели (см. рис.2) в верхней части частотной плоскости вырезать сегмент под углом 0 = mod„((p + 7c/2), то еще одно Фурье-преобразование от такого вырезанного спектра даст следующий результат:

^,П)®бК-(м-Р)=еК-а,П-Ю                        (7)

То есть, в выходной плоскости (х',у) отличная от нуля интенсивность будет только в области, соответствующей решетке с углом наклона штрихов ф (с учетом симметрии (х \у) -► (-^-у)).

Причем, этот эффект имеет место независимо от частоты полос, так как им будут соответствовать 8-функции, находящиеся на одном луче - ближе или дальше от центра. Следовательно, вырезая сегмент вдоль направления 0 = modn((p 4- тс/2) мы захватываем спектры от всех решеток с направлением штрихов -ay/P, = tg (р независимо от частоты штрихов и областей, их ограничивающих:

N                          N

w(x, у) = У Ч, (^х.у) cos(a,х+Р,у) —^-» У Q (^ - a,, п - Р,) ->

.=i                                              (8)

• -^А^ ^а (^ - а,, n - Р J -^ У q_k (-Х -у) = D^x,у) кеК                           к^К

где D^x.y^ совокупность всех областей, где линии изображения w(x,y) направлены под углом ф.

Таким образом, вращая щель и вырезая сегменты в верхней части Фурье-плоскости, мы можем просканировать все направления линий, имеющиеся на изображении в диапазоне [0,л).

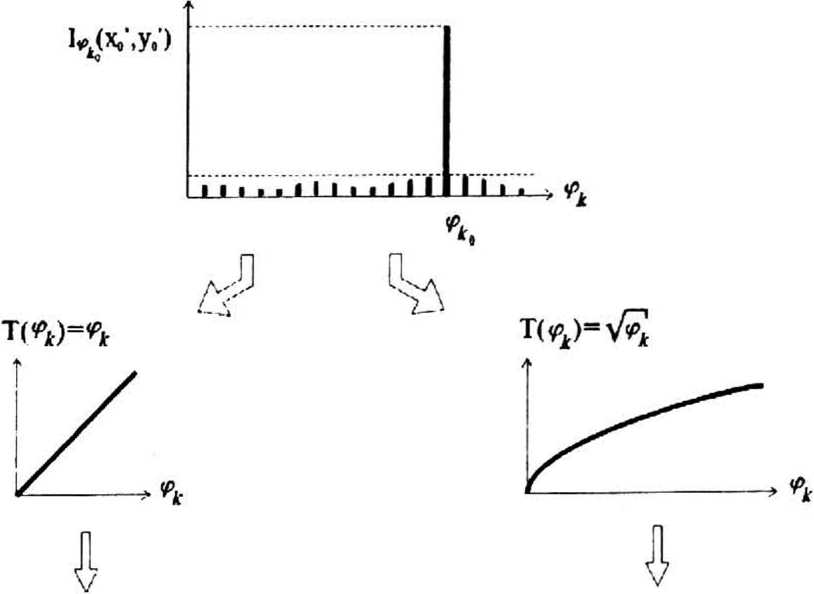
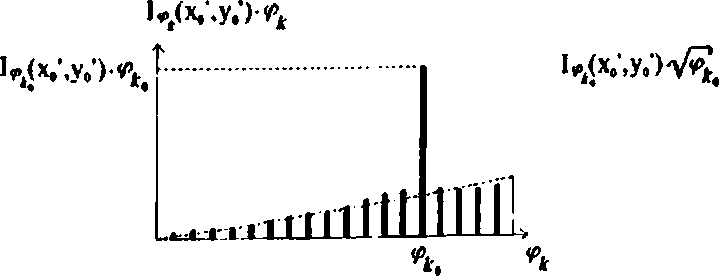
• 12,    Маркировка углов.

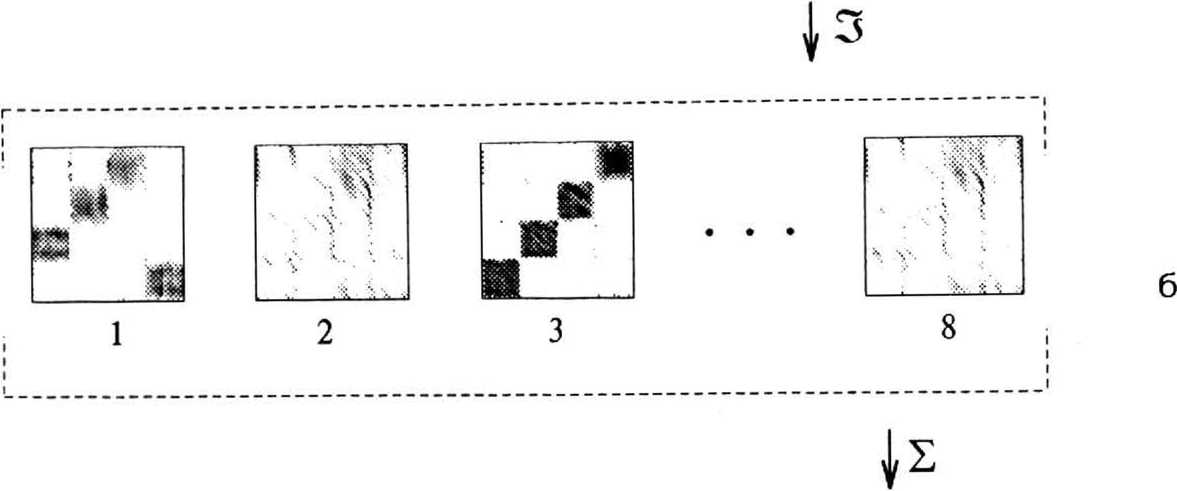
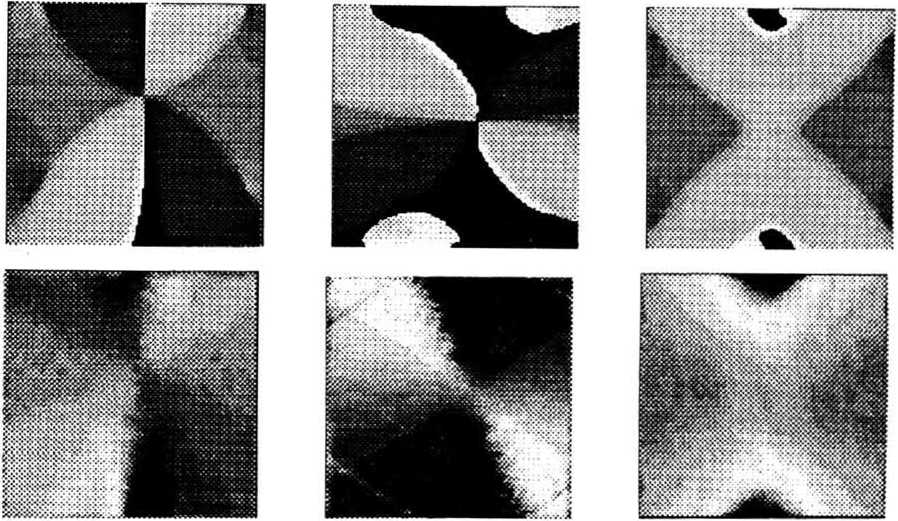
Чтобы идентифицировать области, соответствующие различным направлениям, их нужно маркировать.

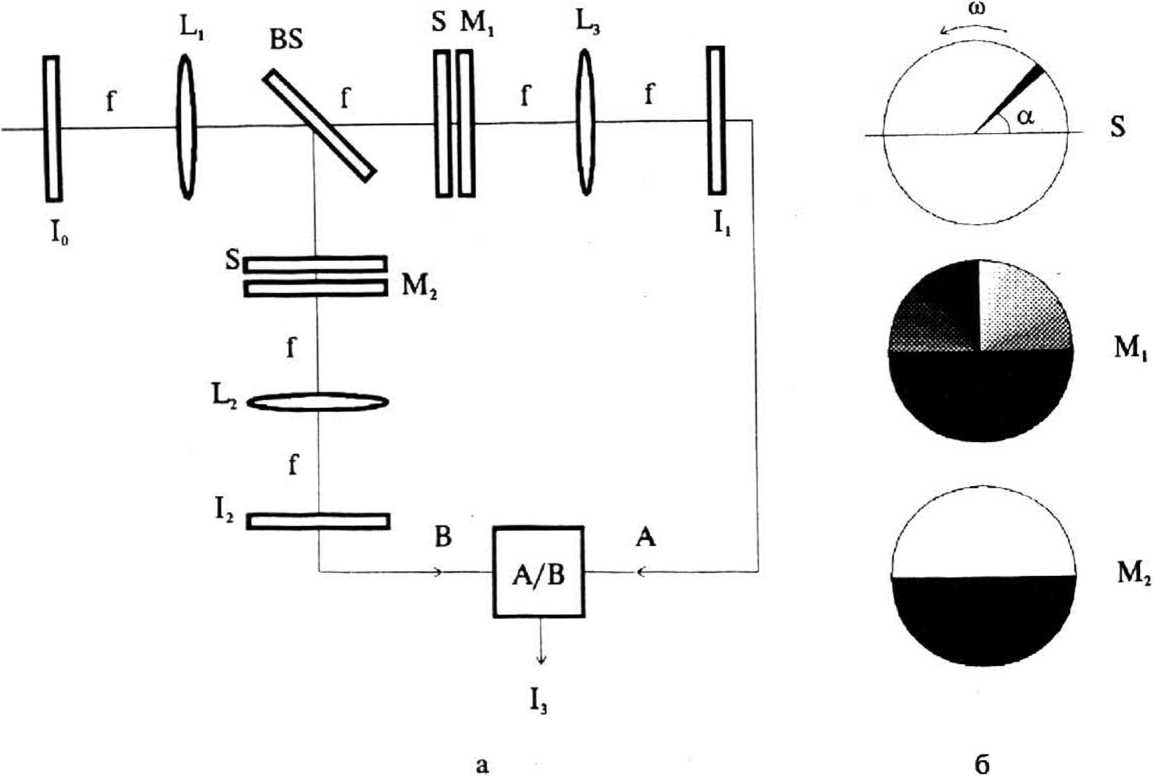
Проще всего было бы ненулевым областям, полученным при положении щели под углом 0 = mod_n(

ф, то есть выполнить преобразование:

/’„«У)

Ф, /,«У)*о ' о, /ф(х',У) = О

И тогда сумма всех РДх^У), ф е[0, л) даст поле направлений исходного изображения.

Однако, сложность состоит в том, что ’’нулевая” область на самом деле имеет хоть и близкую, но все же отличную от нуля интенсивность. Следовательно, появляется необходимость определения некоторого порога d для корректировки процедуры (9):

P^yV

Ф, ^d О, I^x\y^

(Ю)

что значительно усложняет весь процесс, так как значение порога d различное для каждой вновь получаемой картины 7_ф(х',У) .

Поэтому предлагается проводить следующую процедуру:

Сканируя вращающейся щелью с некоторым дискретным шагом Аф, мы получим 7_ф(х',у) для М значений ф:

^Дх\у'\ ф^ = Дф.(*-]), Дф = 77, к = \,М               (11)

Суммируем их с весами, являющимися соответствующим углом:

^«У^^Л.КУУф,              <|2>

*=1

Оптически такую процедуру можно выполнить, установив непосредственно за экраном с щелью амплитудную маску с функцией пропускания (с учетом (11)):

Ф^

Дф .1^1 Дф , —г^ фь--^mod, а + — +<ф. + — Д -\,М

2 V 2/         2

Дф                 Дф ф., + — < mod, а + — < 2тг--

" 2      4   2/      2

В сумме (12) для некоторой точки (х₀',^₀') одна из компонент 1^ (Xq*,^/), угол которой ф^ совпадает с направлением линий в соответствующей точке (х₀,^₀) на изображении, будет значительно больше по величине, чем остальные компоненты (см. рис.З). Таким образом, ^(хДдУ) * /^Хо'.^Уф^ .

Теперь, чтобы выделить угол, нужно провести следующую нормировку выражения

5m(x' v')

^^-"^"Д,              (14)

5(х',у)

где SUVy^^J^yxVy) t=i

Действительно, в соответствии с предыдущими рассуждениями ^(Хо1,^') 28 /^(х,,',^') , а следовательно,

4<^хо -У» ) * ~      ,--— = Ф», * Ф^о.Ло)

То есть, G^x\y) = ф(х,^) и представляет собой поле направлений исходного изображения.

Однако, линейное кодирование имеет определенные недостатки. В этом случае веса для компонент, соответствующих высоким значениям угла значительно больше, чем для компонент с низким значением угла. То есть, происходит смещение всего диапазона в сторону высоких значений угла наклона (см. рис. 3). Поэтому следует применять менее “смещающие” функции Цф*):

м

W.y'^'LU-^’-y'VT^^               (16)

*=1

например, Г(ф^) = y/ip_t (см. рис. 3).

Ь/хДУо’)

а

■ гипгГПГПП п, ^

б

Рис.З. Маркировка углов с помощью амплитудного (а) линейного и

• (б)    нелинейного фильтров.

Более того, в целях повышения эффективности пропускания светового пучка, а также, чтобы избежать описанных выше недостатков, предлагается использовать вместо амплитудной маски чисто фазовую:

т(а) = •

Дф

, х Аф                        Дф z г~г;

ехр(/ф*), ф* m°d^^a + yJ+ <ф4 + —, к = 1,м

7Г

О,

Фа/

Дф

Дф . | л | Дф + —< mod, а+— <2тс--

В этом случае мы получим фазовое поле направлений ^(х1,^*) « ехр[/ф(х,)/)]

• 2.    Оптическая схема построения поля направлений.

На рисунке 4а показана оптико-электронная схема для построения поля направлений.

Рис.4. (а) Оптическая схема вычисления поля направлений с помощью вращающейся щели; (б) непрозрачный экран с щелью и фильтры.

Схема состоит из двух Фурье-корреляторов, в частотные плоскости которых помещены вращающиеся непрозрачные экраны с узкими радиальными щелями (рис. 4б). Излучение разделяется на два канала с помощью расщепителя пучка BS. Линза Li ^с фокусным расстоянием / формирует в плоскостях перед экранами с щелью пространственные спектры исходного изображения 1д(х,у). Комплексная амплитуда света в этой плоскости равна

^,П) = 3{70(х,^)}                           (18)

где (х,у) и (^,п) - декартовы координаты во входной и частотной плоскостях корреляторов, 3{-} - двумерное преобразование Фурье. Сразу за экраном с щелью сформируется световое поле с амплитудой

Л^П) = ^,n)S a-arctg

где 8(х) - функция Дирака, 0<а<2п - полярный угол, задающий мгновенное направление щели.

Амплитудные маски М] и М2 (рис. 46) предназначены для отсечения половины углов л<а<2л и для линейного кодирования выделенных направлений пропорционально углу. Пропускание этих масок имеет соответственно вид:

Аф . f я ф,--< mod. а + —

2 Я1 2,

Аф , f л' Фм+— ^т«Ца + -

Фк+^^-ЦМ

2л-^

т2(г,а) = ^

1,

О,

О < а < л - Аф, 2л - Аф < а < 2л

л- Аф <а <2л-Аф

£=r-cosa, r| = r sina

Если на выходе горизонтального Фурье-коррелятора расположено матричное фотоприемное устройство (например, ПЗС-камера), время регистрации которого кратно числу полных оборотов экранов с щелью 5, то выходное изображение Ii(x,y) будет описываться распределением интенсивности (14), где 7(ф*) = ^Ц)_к • Аналогично для вертикальной ветви на выходе сформируется изображение 7/х,у), распределение интенсивности которого описывается выражением (14) с Цф^) = 1 •

Оба изображения в виде аналоговых сигналов построчно поступают на делительное устройство (рис.4), которое формирует результирующий сигнал, пропорциональный величине <р(х,у).

• 3.    Вычислительные эксперименты с модельными изображениями

Для исследования эффективности предлагаемого оптического метода построения поля направлений был проведен ряд вычислительных экспериментов.

Спектр модельного изображения (см. рис.5а) сканировался сегментами различной ширины. Ширина сегментов Дф, от которой зависит и их количество Л/=л/Дф, должна быть такой, чтобы захватывать главную часть спектров, соответствующих определенному направлению, и в то же время не включать спектры других направлений.

Из рис. 5а и 56 видно, что сегмент 2 захватил “хвосты” Sinc-функций из сегментов 1 и 3, в следствии чего появились небольшие всплески интенсивности в соответствующих областях в выходной плоскости. В рассмотренном примере влияние излишней ^М— 8), как и недостаточной сегментации (Л/=2), хорошо видно из рис. 5в.

a

М=2

M=4

M=8

Рис.5 Компьютерное моделирование оптического метода: (а) модельное изображение и его спектр, (б) селекция направлений при М=8 сегментах, (в) поля направлений, построенные при М=2,4,8 сегментах, соответственно.

Результаты, полученные с помощью оптического метода сравнивались с результатами, полученными цифровым дисперсионным методом. На Рис.6а представлены модельные изображения типа интерферограмм, на Рис.66 — их поля направлений, полученные дисперсионным методом и затем отфильтрованные особым способом [3] (Рис.бв) с целью увеличения числа градаций, а на Рис.6г - поля направлений, полученные с помощью оптического метода.

Дисперсионный метод хорошо работает только при малом количестве направлений на изображении, так как отслеживает только четыре угла. Однако, сложных изображениях присутствует, как правило, большое количество направлений, и в этом случае, как видно из рис.6 значительное число градаций в дисперсионном поле направлений “съедается”, восстановить которые не помогает даже специальная фильтрация.

6" то же время оптический метод дает достаточно хорошие результаты как при малом, так и большом количестве направлений, хотя разграничение углов не такое четкое, как в дисперсионных полях направлений, что объясняется перекрытием спектров от разных направлений.

а

б

Рис.6 (а) Интерферограммы и их поля направлений, построенные различными методами: (б) цифровым дисперсионным, (в) цифровым дисперсионным с фильтрацией и (г) оптическим.

Рис.7 Пространственные спектры для соответствующих (а) интерферограмм и (б) оптических полей направлений.

При структурировании контурного изображения происходит уменьшение ширины пространственного спектра, что хорошо видно из рис.7. На рис.7а представлены Фурье-спектры для интерферограмм (рис.ба), а на рис.76 представлены Фурье-спектры для их полей направлений, построенных оптическим методом (рис.бг).

• 4,    Вычислительные эксперименты с натурными изображениями,

• 4.1.    Расчет параметров оптической схемы.

Для проведения вычислительных экспериментов с натурными изображениями с дактилоскопических карт в ЭВМ с помощью сканера вводились отпечатки пальцев.

На рис.8 представлено дактилоскопическое изображение (рис.8а), его Фурье-спектр (рис.86) и поле направлений, построенное оптическим методом (рис.8в).

а                     б                        в

Рис.8 (а) Дактилоскопическое изображение, (б) его пространственный спектр и (в) оптическое поле направлений.

Считая, что отпечаток пальца имеет размер 5= 15+20 мм, а толщина папилярных линий />=0.5 мм, определим конкретные параметры описанной во втором разделе оптической схемы. Ширину спекла в частотной плоскости можно считать по формуле

А= (22)

где X - длина волны источника (для лазера с красным светом Х=0.63 мкм), f - фокусное расстояние, R - радиус изображения (для отпечатка пальца R = 10 мм).

Интересующая нас часть спектра будет находится на расстоянии х = & L от центра, где L - S/p - число папилярных линий на отпечатке пальца. Для / = 100 мм - х=0.2 мм, при этом для удобства вращения экран с щелью, установленный в частотной плоскости, может значительно превышать этот размер, необходимо лишь, чтобы щель была прорезана достаточно глубоко и захватывала нужную часть спектра.

• 4.2.    Вычислительный эксперимент по распознаванию.

Для выработки практических рекомендаций по решению задачи персональной идентификации с помощью дактилоскопических изображений было отобрано 10 близких по узору отпечатков пальцев, несколько реализаций которых составляли класс.

Распознаванию подвергались как сами дактилоскопические изображения (рис.9а), так и их поля направлений, построенные цифровым дисперсионным методом (рис.96) и отфильтрованные (рис.9в), а также построенные оптическим методом (рис.9г).

б                     В                     Г

Рис.9 (а) Дактилоскопические изображения и их поля направлений, построенные методами: (б) цифровым дисперсионным, (в) цифровым дисперсионным с фильтрацией и (г) оптическим.

При использовании разложения Карунена-Лоэва [4,5] были получены следующие результаты. Сами дактилоскопические изображения не поддавались распознаванию (имела место 70% ошибка при обработке даже /.= 100 коэффициентов разложения), что не только оправдывает, но и делает необходимым применение структурных методов при анализе таких сложных изображений.

Поля направлений, полученные дисперсионным методом, полностью распознавались при 1^34 коэффициентах, в то время как отфильтрованные поля направлений при том же количестве коэффициентов давали ошибку 20%. Такую ситуацию можно объяснить слишком сильным сглаживанием при фильтрации, “съедающим” некоторые мелкие, но существенные детали.

Для уверенного же распознавания полей направлений, построенных с помощью моделирования оптического метода, понадобилось Л>12 коэффициентов, что почти в три раза меньше, чем при использовании дисперсионного метода. Из рис.9 видно, что оптический метод по сравнению с дисперсионным дает более сглаженные поля направлений (следовательно, нет необходимости в фильтрации), и в то же время сохранившие все важные детали.

Таким образом, структурирование контурных изображений позволяет уменьшить количество признаков, адекватно описывающих изображение, что можно проследить также по уменьшению отклонения

5 = Цн^х)-w(x)|| ^)

между исходным изображением w(x) и восстановленным по фиксированному коли ,сству К коэффициентов разложения Фурье:

w(x) = ^wt/t(x). (24)

На рисунке 10 в верхнем ряду показаны исходные изображения в^х) рассматриваемых типов, а в нижнем - 1юсстановленныс по Л=4000 коэффициентам Фурье и'(х). Отклонение 6 (23) составило для дактилоскопического изображения (рис. 10а) - 6=0.32. дисперсионного поля направлений (рис.Юб) - 6=0.25, отфильтрованного дисперсионного поля направлений (рис.Юв) 6=0.15 и оптического поля направлений (рис.Юг) - 6=0.11.

Рис. 10 (а) исходные изображения и (б) восстановленные по 4000 коэффициентам разложения Фурье.

Таким образом, применение оптического метода позволяет наиболее сильно сократить число анализируемых признаков повысить эффективность обработки изображений.

Заключение

Переход от контурных изображений к полям направлений позволяет провести структурирование такого изображения, выделив тем самым наиболее важную информацию и резко сократив количество признаков адекватно описывающих изображение, что в конечном счете, упрощает процедуру анализа сложных контурных изображений.

Экспериментальное исследование разработанного оптического метода построения полей направлений подтвердило работоспособность предлагаемого метода. Таким образом, можно говорить о существовании оптического метода структурирования контурных изображений типа интерферограмм и дактилограмм, представляющего особую актуальность во многих задачах оптической обработки изображений.

Результаты вычислительного эксперимента по распознаванию дактилоскопических изображений показали необходимость применения структурных методов при анализе таких сложных изображений, а также эффективность разработанного оптического метода по сравнению с цифровым дисперсионным методом.

Л и т с р а т у р а.

• 1.    Soifer V.A., Khonina S.N., Ilyasova N.Yu., and Kotlayr V.V. Structural methods in pattern recognition using optical Karhunen-Loeve Expansion.// Proceedings of SSPR’94, 1994.

• 2.    Khonina S.N., Soifei V.A. and Dvoryanova T.P. A method for detecting disturbances in microcrystal structure of tear specimen // Proceedings of DIP’94, 1994.

• 3.    H.K). Ильясова, А.В. Устинов, А.Г. Храмов. Методы анализа дактилоскопических изооражений на основе поля направлений. // Научное приборостроение 1993, т.З. No.l.

• 4.    V.A. Soifer, M.A. Golub and S.N. Khonina, Dccorrelated Features of Images Extracted with the Aid of Optical Karhuncn-Loeve Expansion // Pattern Recognition and Image Analysis, 1993, vol.3, No.3, pp.289-295.

• 5.    V.A. Soifer and S.N. Khonina, Stability of the Karhunen-Loeve Expansion in the Problem of Pattern Recognition // Pattern Recognition and Image Analysis, 1994, vol.4, No.2, pp.137-148.

СПРАВОЧНИК

"Высшие учебные заведения Москвы и Московской области"

Международный центр научной и технической информации (МЦНТИ) выпустил уникальный справочник по вузам Москвы и Московской области на русском и английском языках. Справочник содержит сведения о 88 государственных и 50 негосударственных вузах, имеющих лицензии на право образовательной деятельности в сфере высшего образования. Объем справочника - 139 стр.

Справочник состоит из двух частей:

Информация о высших учебных заведениях включает: полное наименование вузов, имена ректоров, сведения о количестве преподавательского состава, перечень специальностей, почтовый адрес, телефоны, факс, телекс.

По негосударственным учебным заведениям приводится информация о продолжительности обучения и другие сведения.

Указатель специальностей представляет собой двухуровневый рубрикатор специальностей, в котором для каждой специальности содержится список всех высших учебных заведений Москвы и Московской области, готовящих по ней специалистов.

Алфавитный указатель учебных заведений имеет ссылку на страницу, где находится полная информация об учебном заведении.

Раздел "Таблица соответствия старых и новых наименований государственных учебных заведений" позволяет ориентироваться в справочнике, если известно только старое наименование вуза.

Стоимость справочника 6 долларов США за 1 экземпляр или рублевый эквивалент по курсу ЦБ РФ на момент оплаты справочника.

Банковские реквизиты МЦНТИ:

при расчетах по Москве и Московской области:

МЦНТИ, р/с 900603538 в АКБ "Кредит-Москва", МФО 997191, код участника 7М;

при иногородних платежах:

МЦНТИ, р/с 900603538 в АКБ "К[)едит-Москва", корр. счет 501161700 в ГРКЦ Г У ЦБ РФ по г. Москве, МФО 201791, код участника 83.

Адрес: 125252, Москва, ул. Куусинена, 216, МЦНТИ, СОПИ

Тел.: (095) 198-73-41, 198-72-10

Факс (095) 943-00-89