Оптический модулятор на основе связанных фотонно-кристаллических резонаторов

Реализация оптических компонентов обработки сигналов на кристалле является важным шагом в развитии вычислительной техники. Одним самых востребованных компонентов такой обработки является оптический модулятор. В последнее время достигнуты существенные результаты в улучшении этих устройств. Например, пропускная способность оптических модуляторов увеличилась с МГц до ТГц менее чем за 10 лет [1]. Тем не менее, остаётся ряд проблем. В частности, необходимо уменьшить количество энергии на бит передаваемой информации, а также сократить размеры устройства. Всё это должно быть достигнуто с использованием КМОП(CMOS)-совместимых процессов изготовления. Фотонно-кристаллические структуры получили широкое распространение в качестве платформы для реализации различных нанофотонных элементов [2]. Предложено несколько решений задачи оптической модуляции на основе фотонно-кристаллических структур. В работе [3] описан фотонно-кристаллический лазер с возможностью высокочастотной модуляции. В работах [4, 5] представлены оптические модуляторы на основе оптической накачки. В работе [6] предложен фотоннокристаллический модулятор на основе электронной накачки. В данной работе описан компактный оптический модулятор на основе связанных фотонно-кристаллических резонаторов с возможностью модуляции в области малой интенсивности резонансной моды.

1.    Постановка задачи

На рис. 1 показана схема оптического волновода из двух связанных через волновод резонаторов. Здесь переменная к, j = {1,2} обозначает коэффициенты связности j-го резонатора с волноводом, rj = {1, 2} – коэффициенты энергетических потерь j-го резонатора в пространство, pin, prf, ptr – амплитуды входного, отражённого и прошедшего полей соответственно. В соответствии с временной теорией связанных мод [7], резонаторы мо- гут характеризоваться, во-первых, добротностью Q, во-вторых, временем жизни (lifetime) т. В данной работе для сокращения нотации потери резонатора описываются величинами, которые являются обратными времени жизни.

Рис. 1. Схема оптического волновода из двух связанных через волновод резонаторов

Система, изображённая на рис. 1, может быть интерпретирована как резонатор Фабри–Перо. Функции пропускания зеркал в этом резонаторе определяются функцией пропускания одного резонатора. Согласно временной теории связанных мод, функцию пропускания одного резонатора можно записать в виде

• , .       2к,                                         , .

T ( j ) =---- j— , S j = i ( ®-® j ) + j j = { 1,2 } , (1)

sj + 2k j где toj, j ={1,2} - резонансная частота j-го резонатора. Добротность j-го резонатора Qj определяется соотношением 1/Qj =1/Qj к + 1/Qr, где Qj K = Oj /(4к) и Qjr = o /(2 rj).

Функция пропускания резонатора Фабри–Перо с зеркалами, которые обладают функциями пропускания T ₁ и отражения 1 – T ₁, записывается в виде

T ( S 1 ) T ( s 2 ) I i ⁶

T 2 ( S 1 , s 2 ) - pt^ = p_in

1 - ( 1 - T 1 ( s ) )( 1 - T 1 ( s 2 ) ) I i ²⁶ ’

где 6 - набег фазы в волноводе, который связывает резонаторы. Дисперсией волновода мы здесь пренебрегаем.

2.    Исследование параметров оптического модулятора

Масштабирование уровня энергии переключения

На рис. 2 штриховой линией показана функция пропускания одного резонатора. Добротность этого резона- тора Q =1200, резонансная длина волны Х0=1,488 мкм. Внешние потери данного резонатора определяются величиной Qjr = 3,2×105. Сплошной линией на рис. 2 показана функция пропускания массива двух таких же связанных между собой резонаторов. На рисунке набег фазы в связывающем резонаторы волноводе составляет 6=п/2. Такой набег фаз соответствует ситуации, при которой связывающий волновод отсутствует.

Динамическая подстройка набега фаз 6 может быть реализована изменением индекса рефракции волновода. Для этого может быть использован, например, эффект Керра, температурное воздействие или инъекция свободных носителей ( free carriers ). В работе [4] для динамического управления добротностью резонатора использовался последний способ. Применялась импульсная оптическая накачка, чтобы изменять набег фаз в кремниевом фотонно-кристаллическом волноводе в диапазоне от 0 до п . При использовании лазера с длиной волны 0,775 мкм это потребовало энергии около 20 пДж.

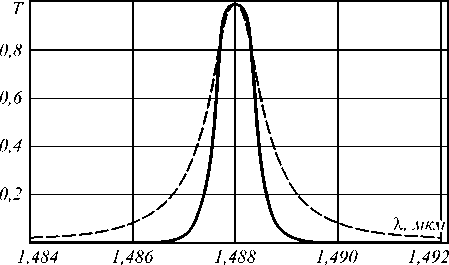
Рис. 2. Функции пропускания одного резонатора (штриховая линия) и двух связанных резонаторов при 9=П2 (сплошная линия)

резонансных мод резонаторов. Для ситуации, при которой связывающий волновод отсутствует, 6 = п /2, такое рассогласование резонансных мод приводит к существенному изменению функции пропускания.

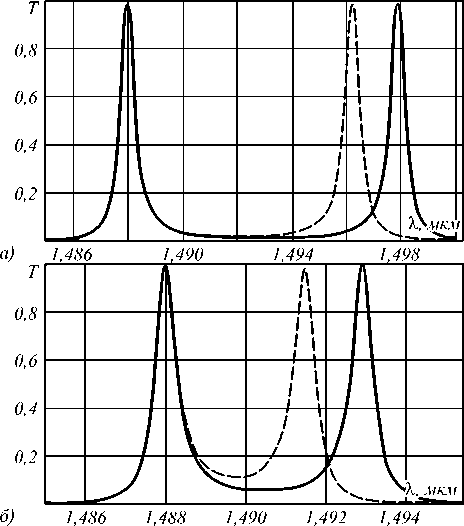
Рис. 3. Функции пропускания двух резонаторов при набеге фаз в волноводе 9=П 50 (сплошная линия) и 9=П 50+ П 250 (пунктирная линия) (а), при набеге фаз в волноводе 9=П 25 (сплошная линия) и 9=П 25+ П 125 (пунктирная линия) (б)

Сплошной линией на рис. 4 показана функция пропускания двух резонаторов с вырожденными резонансными модами на длине волны % ₀= 1,488 мкм при 6 = п /2. Если резонансная мода в одном из резонаторов смещается на 1 нм ( Х ₀= 1,487 мкм), то функция пропускания претерпевает значительные изменения (штриховая линия на рис. 4). Эти изменения становятся ещё большими, если рассогласование резо-

Для реализации предлагаемого в данной работе оптического модулятора нет необходимости изменять набег фаз в столь широком диапазоне. На рис. 3 а показаны функции пропускания двух резонаторов при набеге фаз в волноводе 6 = п /50 (сплошная линия) и 6 = п /50 + п /250 (пунктирная линия). Видно, что, во-первых, для значений 6, отличных от п /2, вырожденные моды двух резонаторов разделяются. Величина разделения мод составила 10 нм для 6 = п /50. Во-вторых, для смещения по частоте одной резонансной моды на свою ширину необходим дополнительный набег фаз только на величину п /250.

На рис. 3 б показаны функции пропускания двух резонаторов при набеге фаз в волноводе 6=п /25 (сплошная линия) и 6=п /25 + п /125 (пунктирная линия). Величина разделения мод здесь составляет 5 нм для 6=п /25. Таким образом, предлагаемая в данной работе модель оптического модулятора предполагает возможность масштабирования как количества энергии накачки, так и величины спектрального разделения резонансных мод.

Связанные резонаторы с невырожденными резонансными модами

Погрешности при изготовлении связанных резонаторов влияют, прежде всего, на смещение частот нансных мод составляет 2 нм (%0= 1,486 мкм) - то-

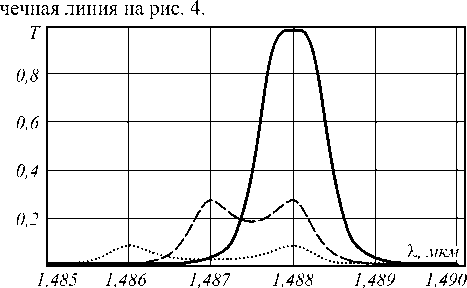
Рис. 4. Схема оптического волновода из двух связанных через волновод резонаторов

Добавление в эту схему связывающего резонаторы волновода кардинально меняет ситуацию. На рис. 5 а , б показаны функции пропускания резонаторов, параметры которых соответствуют параметрам функций пропускания резонаторов на рис. 4 а , б .

Единственное отличие заключается в том, что на рис. 5 резонаторы настроены на различные частоты. Резонансная частота одного резонатора равна 1,488 мкм, другого – 1,486 мкм.

Видно, что различия между функциями пропускания на рис. 4 и 5 не носят кардинального характера. Причём эти отличия тем меньше, что меньше начальный набег фаз в волноводе. Таким образом, модель предлагаемого в данной работе оптического модулятора допускает существенные ошибки при изготовлении.

3.    Расчёт оптического модулятора на основе фотонно-кристаллических резонаторов

Рассчитаем параметры конкретного ФК-резонатора, выполняющего интегрирование оптического сигнала. В качестве такого резонатора выберем элемент на основе гребенчатого ФК-волновода. По сравнению с двумерными ФК-структурами в слое [4] резонаторы на основе гребенчатого ФК-волновода обладают меньшей площадью и естественным образом интегрируются в волноводную геометрию соединений на кристалле. На рис. 6 а показан один из вариантов резонатора на основе гребенчатого ФК. Здесь дефект, в котором возбуждается резонансная мода, формируется уменьшением радиуса отверстий в окрестности дефекта.

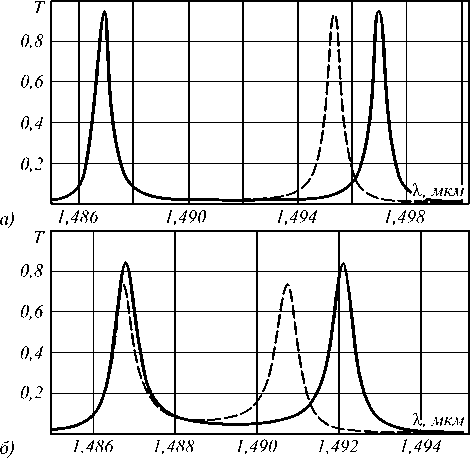
Рис. 5. Функции пропускания двух рассогласованных (резонансы на 1,488 мкм и 1,486 мкм) резонаторов при набеге фаз в волноводе θ = π /50 (сплошная линия) и θ = π /50 + π /250 (пунктирная линия) (а), при набеге фаз в волноводе θ = π /25 (сплошная линия) и θ = π /25 + π /125 (пунктирная линия) (б)

Для расчёта характеристик резонатора использовался двумерный метод FDTD [8]. На рис. 6а введены обозначения геометрических параметров одного резонатора из массива. Волновод имеет ширину w = 500 нм и состоит из материала с индексом рефракции, равным 2,97. Такая величина соответствует эффективному индексу рефракции волновода из кремния толщиной 270 нм, который лежит на стеклянной подложке и окружён воздухом. Несмотря на то, что в данной работе рассматрива- ется кремниевый волновод, множество других материалов может быть использовано для реализации фотоннокристаллического резонатора. Отверстия в регулярной части волновода заполнены воздухом, имеют диаметр 185 нм и отстоят друг от друга на a = 350 нм. В табл. 1 содержатся значения радиусов отверстий и периода решётки в зоне дефекта. Эти геометрические параметры обеспечивают возникновение энергетической запрещённой зоны (bandgap) для TE-поляризации в волноводе. Длина волны резонансной моды равна 1,488 мкм. Добротность резонатора с 4 регулярными отверстиями с каждой стороны равна 1230. Внешние потери данного резонатора определяются величиной Qjr =3,19×105.

ТГгЛ'

(OOOOOOO-t- - I 4*0 000000/

• а)                           I

  б)

  
  

  Hreg/2

  ( OOP

  

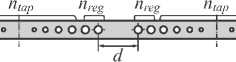
  ii_reg/2

  POO /

  
  

• в) ______PjpM*»||ll<|o4Mji>^^______

Рис. 6. Схема резонатора на основе ФК-волновода (а), массив из двух таких резонаторов (б), распределение амплитуды электромагнитного поля (в)

На рис. 6 б показан массив из двух фотонно-кристаллических резонаторов, связанных волноводом длиной d .

Табл. 1. Геометрические параметры ФК-резонатора на рис. 6a

a 1	b 1	a 2	b 2	a 3	b 3	a 4	b 4
130	200	160	290	180	310	185	304

Инъекция свободных носителей может быть как оптической, так и электронной. Накачка выполняется в связывающий волновод посередине между двумя резонаторами. Как показывает рис. 6 в , амплитуда возбуждаемых резонансных мод в этой области минимальна. Поэтому введение свободных носителей практически не ухудшает добротность резонансных пиков. В работах [4, 6] описаны оптические модуляторы, в которых оптическая и электронная накачки выполнялись в области резонансной камеры. Т.е. в зоне максимальной амплитуды резонансной моды. В работе [6] использовалась оптическая накачка импульсным (3 пс) лазером мощностью 10 мкВт, чтобы сдвинуть спектральный пик на его ширину.

Найдём соответствие между набегом фаз θ и длиной d (рис. 6б) связывающего резонаторы волновода для рассчитанных фотонно-кристаллических резонаторов. Длина волны резонансной моды в волноводе равна 1448/2,97=500 нм. Тогда дополнительный набег фаз величиной π/2 соответствует дополнительному фрагменту волновода длиной 500/4 = 125 нм. Отсутствие связывающего волновода (θ = π/2) соответствует значению d =350 нм. Однако полное соответствие между аналитическим выражением (2) при θ = π/2 и результатом FDTD-моделирования достигается при d =370 нм. Это может быть вызвано тем, что брэгговская частота фотонно-кристаллического волновода не совпадает с резонансной частотой. В этом случае, чтобы реализовать условие θ = π/2, требуется добавить фрагмент волновода между резонаторами [9].

На рис. 7 а показаны функции пропускания двух резонаторов для связывающего волновода длиной d =490 нм (сплошная линия) и d =489 нм (пунктирная линия). Эти параметры примерно соответствуют параметрам аналитических графиков на рис. 3 а . Видно, что FDTD-моделирование также показывает возможность смещения спектрального пика на его ширину на полувысоте. Величина разделения мод для FDTD-моделирования также составила примерно 10 нм.

На рис. 7 б показаны функции пропускания двух резонаторов для связывающего волновода длиной d =484 нм (сплошная линия) и d =480 нм (пунктирная линия). Величина разделения мод здесь составляет примерно 5 нм. Понижение максимумов спектральных пиков на рис. 7 а , б может быть вызвано как дискретностью рассчитываемых отсчётов длин волн, так и потерями на границе резонаторов и связывающего их волновода. На рис. 7 а , б также присутствуют моды резонатора Фабри–Перо соседнего порядка.

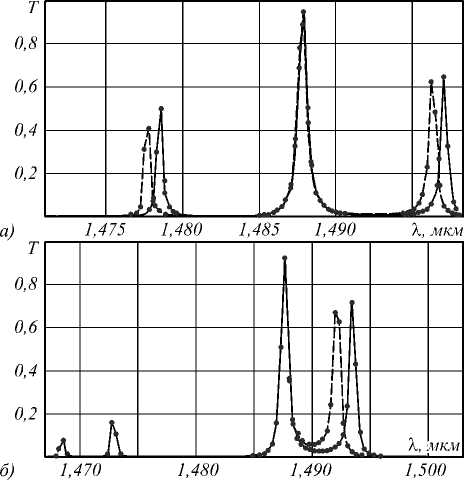
Рис. 7. Функции пропускания двух резонаторов для связывающего волновода длиной d = 490 нм (сплошная линия) и d = 489 нм (пунктирная линия) (а), для связывающего волновода длиной d = 484 нм (сплошная линия) и d = 480 нм (пунктирная линия)

Таким образом, FDTD-моделирование подтвердило возможность масштабирования количества энергии накачки свободных носителей. Минимальное значение энергии накачки определяется величиной свободной спектральной зоны, которая для фотонно-кристаллических резонаторов задаётся размером запрещённой зоны. Численное моделирование показало, что рассчитанный в данной работе резонатор обладает свободной спектральной зоной шириной около 300 нм. Поэтому требуется обеспечить фазовый сдвиг величиной 10-5 π, чтобы сместить резонансный пик на его ширину. Для оценки количества энергии Eπ, необходимого для получения фазового сдвига на π, можно ориентироваться на результаты, которые получены в работе [4]. Если, например, принять Eπ = 40 пДж, то фазовый сдвиг на 10-5 π обеспечивается количеством энергии, примерно соответствующим накачке, которая использовалась в работе [6]. Однако, в отличие от работы [6], здесь накачка свободных носителей реализуется в области малой амплитуды резонансной моды. Это позволяет как минимизировать влияние свободных носителей на объекты в области резонансной камеры, в частности, квантовые точки, так и реализовать эффективную электронную накачку. Электроды, обеспечивающие такую накачку, могут располагаться в непосредственной близости от области накачки, в отличие от ранее предложенных схем, например, в работе [6]. Для тонкой настройки первоначального набега фаз θ в волноводе можно использовать, например, варьирование температуры волновода.

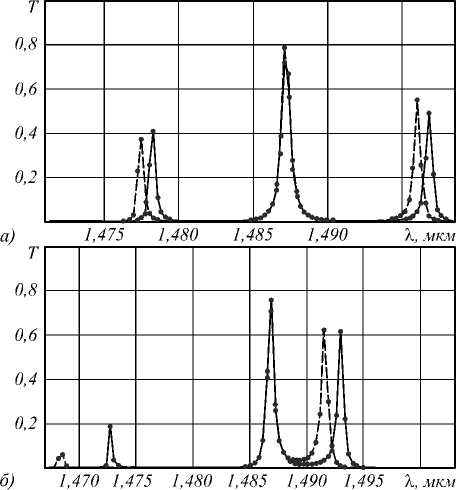
Рис. 8. Функции пропускания двух рассогласованных (резонансы на 1,488 мкм и 1,486 мкм) резонаторов для связывающего волновода длиной d = 490 нм (сплошная линия) и d = 489 нм (пунктирная линия) (а), для связывающего волновода длиной d = 484 нм (сплошная линия) d = 480 нм (пунктирная линия) (б)

Исследуем влияние погрешностей изготовления предложенной модели оптического модулятора. Для этого изменим резонансную длину волны одного из двух резонаторов. При уменьшении диаметров пары центральных отверстий резонансной камеры со 130 нм до 127 нм резонансная длина волны сдвигается примерно на 2 нм и принимает значение 1,486 мкм. Таким образом, оптический модулятор состоит из двух резонаторов с резонансными длинами волн 1,486 мкм и 1,488 мкм.

На рис. 8а показаны функции пропускания двух рассогласованных резонаторов для связывающего волновода длиной d =490 нм (сплошная линия) и d =489 нм (пунктирная линия). Видно, что рассогласованность резонато- ров незначительно исказила функции пропускания по сравнению с рис. 7а. Аналогичный вывод можно сделать, сравнивая рис. 7б и 8б для функций пропускания двух рассогласованных резонаторов для d =484 нм (сплошная линия) и d =480 нм (пунктирная линия).

Заключение

Предложен и численно исследован оптический модулятор. Модулятор состоит из двух связанных фотонно-кристаллических резонаторов. Показана возможность масштабирования как количества энергии накачки, так и величины спектрального разделения резонансных мод. Продемонстрирована высокая устойчивость предложенного устройства к погрешностям изготовления связанных резонаторов. Рассчитан компактный оптический модулятор на основе фотонно-кристаллического волновода. Показано, что предложенная модель модулятора позволяет реализовать модуляцию в области малой интенсивности резонансной моды. Это позволяет как минимизировать влияние свободных носителей на объекты в области резонансной камеры, в частности, квантовые точки, так и реализовать эффективную электронную накачку.

Работа выполнена при поддержке грантов РФФИ №№ 13-07-97002, 13-07-13166, 14-07-97008, 14-07-97009 и Программ №№ 2 и 5 фундаментальных исследований ОНИТ РАН, Министерства образования и науки РФ.