Оптический отклик твист - индикатора при двумерной упругой деформации жидкого кристалла, вызванной электрическим полем, в зависимости от физических и конструктивных параметров устройства

Широкое использование жидких кристаллов (ЖК) в современных системах отображения информации ставит задачу об адекватном теоретическом описании поведения ЖК во внешнем электрическом поле в зависимости от физических и конструктивных параметров устройства [1-5]. В настоящий момент времени большинство работ в этой области посвящено моделированию характеристик новых ЖК-устройств отображения информации, которые используют при своей работе трех или двух мерные деформации ЖК [3]. Другая большая группа работ посвящена в основном разработке программ и методов расчета оптических характеристик ЖК-устройств при многомерной деформации ЖК во внешнем электрическом поле [4, 5]. В то же время остается открытым вопрос о том, как влияют физические и конструктивные параметры ЖК на видимый размер элемента отображения в устройстве (даже если рассматривать ЖК-индикаторы, использующие самый известный электрооптический эффект – твист – эффект). В случае одномерной деформации ЖК, когда размеры элементов изображения велики (порядка нескольких сотен микрон), такие исследования выполнены в полном объеме [1, 2] и представляют интерес только с точки зрения технологии изготовления. Аналогичные исследования для случая многомерной деформации ЖК, когда размеры элементов изображения имеют линейные размеры менее 70 микрон, не выполнены и остается отрытым вопрос о влиянии физических параметров ЖК на видимый размер элемента изображения устройства с целью определения минимально возможного размера пикселя. В связи с этим данная работа посвящена следующим двум вопросам:

• -    разработке программного средства для расчета двух мерной деформации ЖК во внешнем электрическом поле;

• -    исследованию влияния физических постоянных ЖК и конструктивных параметров устройства на

упругую деформацию ЖК и видимые размеры элемента отображения.

Методика и алгоритм расчета

Моделирование электрооптических характеристик различных ЖК-устройств отображения информации производится в два этапа [1-5]. На первом этапе вычисляется распределение углов ориентации директора ЖК под действием управляющего электрического поля, а на втором вычисляется оптический отклик на данное напряжение, которое прикладывается к управляющим электродам устройства. Остановимся на каждом из двух этапов моделирования электрооптических характеристик ЖК-устройств отображения информации отдельно.

Пусть мы имеем плоскопараллельный слой ЖК (ЖК-ячейку), заполненный немато-холестерической смесью ЖК с положительной диэлектрической анизотропией. На верхней и нижней поверхностях ЖК-ячейки параллельно друг другу расположены несколько длинных электродов. Все электроды предполагались идентичными. Ширина каждого электрода L1, расстояние между соседними электродами L2, толщина ячейки d . Для описания ориентации ЖК в электрическом поле выберем декартову систему координат так, чтобы ось y была направлена перпендикулярно ориентирующим поверхностям, а периодическая структура электродов находится в плоскости x–y. Как известно [1], ориентацию директора ЖК n можно охарактеризовать двумя углами: углом наклона θ молекул ЖК к плоскости x - z и углом поворота ϕ молекул ЖК в этой плоскости. Так как длина электродов значительно больше, чем L1 , L2 , и d , то можно считать, что в направлении z электрод бесконечный. Вся конструкция совмещена с прямоугольной системой координат, начало которой совпадает с центром одного из промежутков между электродами. Ко всем нижним электродам прикладывается потенциал ν =-0, 5⋅V , а ко всем верхним - v = 0,5 • V , где V - управляющее напряжение. Каждые верхний и противоположный ему нижний электроды образуют отдельные пары. Поскольку все пары электродов идентичны, то достаточно найти распределение директора только для одной такой пары. В нашей модели мы считаем, что изменения ориентации директора ЖК n происходят только в плоскости x - у, а вдоль направления z ЖК-слой од нороден. Управляющее поле E при этом направлено параллельно оси у . Тогда равновесное распределение углов ориентации директора n (n = {cos(9) ■ sin(ф),sin(9),cos(9) ■ cos(ф)}) по толщине слоя ЖК, согласно континуальной теории [7-9] достигается при минимальном значении свободной энергии, плотность которой F в данном случае можно записать в следующем виде:

_ 12

F = - (K„(Div(n))2 + K22 (n • Rot(n))

+ K ₃₃( n X Rot ( n ))² - ED );

где K || , K 22 , K 33 - постоянные упругости ЖК; p₀ - естественный шаг спирали ЖК; D , E - индукция и напряженность внешнего электрического поля.

Минимизируя интеграл свободной энергии стандартным образом, получим систему нелинейных дифференциальных уравнений для нахождения распределения углов ориентации директора ЖК 9 ( x , у ) и ф ( x , у ) в электрическом поле.

5 f - 5 9	5 5 x	r			J ^	5 5 у				]	= 0
		I r	5 F				l r	5 F
			d	r 5_ 9 , 5 x
								5	r 5 9 1 5 у	J ^
5 f - 5 ф	5 5 x		d	5 F Гд ф		5 5 у		5	5 F Г 5 ф	1	= 0
5 f - 5 v	d 5 x	I r	d	l д x 5 F r 5 v	J ^	5 5 у	l r	5	l 5 у 5 F r 5 v	JJ 1 1	= 0
		I		l 5 x	J		l		l 5 у	JJ

Эту систему уравнений необходимо решать совместно с граничными условиями, которые в нашем случае жестких граничных условий будут иметь вид: (записаны для случая одной пары электродов окружённых промежутками) нижний электрод:

• 9 = 9 0 , ф = Ф _Т , v =- V /2, при у = 0, и ( L 2 /2) <  x <  ( L 2 /2 + L - ) нижние промежутки:

• 9 = 9 ₀ , ф = Ф _Т , v = 0, при у = 0, и 0 <  x <  ( L 2 /2) и ( L 2 /2 + L - ) <  x <  ( L - + L 2 ) верхний электрод:

• 9 = 9 ₀ , ф = 0 ° ,    v = V / 2, при у = d , и

• (L2/2) < x < (L2/2 + L1) верхние промежутки:

• 9 = 9 ₀,     ф = 0 ° , v = 0,    при у = d , и

• 0 < x < (L2 /2) и (L2 /2 + L1) < x < (Ц + L2), 90 - угол наклона молекул на ориентирующей поверхности, ФТ - угол закрутки ЖК - структуры.

Граничные условия по бокам области определяются исходя из периодичности элементарной ячейки с электродами.

Для удобства численного решения уравнения системы были приведены к безразмерному виду ( x = x / L , у = у / d , L - длина всего электрода ячейки, d - толщина слоя ЖК). Для решения системы уравнений воспользовались наиболее универсальным численным методом - методом конечных разностей [10, 11]. Тогда исходные дифференциальные уравнения заменяются разностными уравнениями относительно сеточной функции. При этом для входящих в уравнение производных используются соответствующие конечно-разностные соотношения. В результате получается система алгебраических уравнений, решая которую, можно найти в узлах сетки значения сеточной функции. Составим конечно-разностную схему для уравнений, для чего введём сетку. Стороны квадрата 0 <  x <  1, 0 <  у <  1 делятся на элементарные отрезки точками x i = i ■ H x (i = 0,1, ^ , n ) и у j = j ■ Н у (j = 0,1,..., m ). Здесь H_x - шаг разбиения по x , Н у - шаг разбиения по у : H_x = 1/ n , Н у = 1/ m , где n и m - количество точек по x и у соответственно. Через точки x i и у j- проведем два семейства координатных прямых x = const и у = const , образующих сетку с прямоугольной ячейкой. Любой узел этой сетки, номер которого (i, j) , определяется координатами ( x i , у j ). Начало системы координат совмещено с точкой (0,0) . Кроме того, в сетку входят также точки с координатами - 1 и n + 1 по x , и - 1 и m + 1 по у . Они необходимы для аппроксимации производных в граничных точках. Далее заменяем производные по формулам конечных разностей. Получившаяся система нелинейных уравнений решалась модифицированным методом простой итерации -методом Гаусса-Зейделя [10]. Начальные приближения задаются из следующих соображений. Полагаем, что в центре электрода решение системы мало отличается от решения аналогичной задачи в одномерном случае. Такая задача в конечно-разностном виде легко получится, если записать уравнения для i = 0 и отбросить все слагаемые, где i отличается от нуля. Полученная система алгебраических уравнений легко решается методом Гаусса-Зейделя.

По краям элемента, где электрод отсутствует (при i = n, i = 0), в качестве нулевых приближений задаем невозмущенное распределение 9, ф и v (9^ = 2° , vП = 0, j = 0...ш). Промежуточные значения для нулевых приближений задаются линейной интерполяцией. В точках (-1, j) , (n + 1,j) значения функций θ , ϕ и ν совпадают (вследствие симметрии задачи) с соответствующими значениями в точках (1, j) , (n - 1,j) для j = 0…m значения функций θ, ϕ и ν в точках (i,1) , (i,m + 1) для i = 0…n задаются методом квадратичной экстраполяции.

На основе описанной выше процедуры были разработан алгоритм и вычислительная программа на языке Compaq Visual Fortran 6.6 . Входными параметрами являются: длина электрода ( L ₁), длина расстояния между электродами ( L ₂) , толщина ЖК-слоя ( d ) , рабочее напряжение ( V ) , упругие постоянные ЖК

(K11 , K22 , K33 ), шаг спирали ЖК-структуры (p0) и компоненты диэлектрического тензора ( ε|| , ε⊥ ).

Вычисление двумерного распределения углов ориентации директора состоит из нескольких шагов. На первом шаге находится одномерное распределение директора по толщине ЖК-ячейки. Для этого в системе уравнений все производные по x прирав- ниваем нулю и заменяем все производные конечноразностными выражениями. Полученная система решается методом Гаусса-Зейделя.

На втором шаге создаются нулевые приближения для двухмерной задачи. Для центра электрода в качестве нулевого приближения используется полученное решение одномерной задачи, для края элемента без электрода задается невозмущенное распределение θ, ϕ и ν. Далее задается начальное распределение θ, ϕ и ν по всей длине элемента для каждого j . После расчёта получаем функции θ(x, y) , ϕ(x, y) и ν(x, y) . Достоверность полученных результатов подтверждалась путем сравнения рассчитанных данных с другими программами [12]. На рис. 1 представлен пример расчета двумерного распределения директора ЖК в электрическом поле для следующих параметров d =4,0 мкм, L1 =35,0 мкм, L2 =35,0 мкм, ε|| =5,5, ε⊥ =4,5, ∆ε=ε|| -ε⊥ =1,0, p0= 80.0, K11=1,010-6 дин, K22=6,0⋅10-7дин, K33=1,5⋅10-6 дин, θ0=20, ФТ=900.

На втором этапе моделирования электрооптических характеристик ЖК-устройств отображения информации рассчитывается оптический отклик устройства. Обычно для расчета оптических характеристик ЖК-устройств отображения информации, которые используют различные электрооптические эффекты, применяются различные матричные методы [8, 13, 14]. Для оценки минимального размера элемента изображения мы предположим, что на устройство падает плоская монохроматическая волна в нормальном направлении.

В таком случае для описания оптических характеристик ЖК-устройства достаточно использовать ме- тод матриц Джонса и матриц когерентности [14]. Предполагается, что в слое ЖК отсутствует многолучевая интерференция, но имеет место интерференция в проводящих и ориентирующих слоях. Данный метод расчета, реализованный в виде отдельного программного модуля, который используется в пакете программ «MOUSE – LCD» [8].

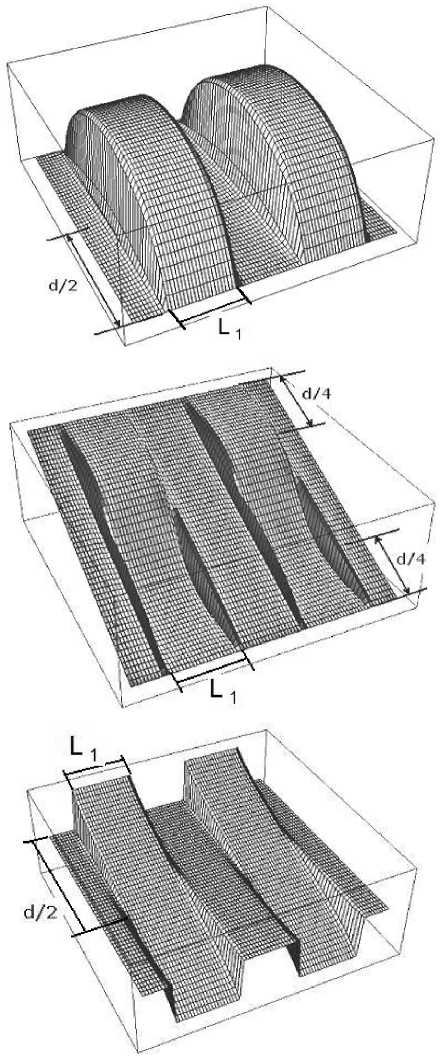
Рис. 1. Рассчитанные двумерные распределения в плоскости x - y для угла наклона директора (а), угла поворота директора (б) и потенциала (в).

Расчёт проводился на области, содержащей две пары электродов. Вычисления проводились для управляющего напряжения 2,0 V c

Результаты и обсуждение

Основными физическими параметрами, которые определяют упругую деформацию ЖК в электрическом поле (и одномерную и двумерную), как известно, являются упругие постоянные материала и его диэлектрическая анизотропия [1, 2]. В качестве конструктивного параметра, определяющего двумерную деформацию ЖК, было выбрано отношение размера электрода к величине межэлектродного зазора. Исследования проводились для ЖК-индикаторов, работающих на основе твист-эффекта, так как такие устройства наиболее широко используются в технике [1, 2]. Из анализа результатов расчета видно, что можно выделить три области деформации ЖК. В первой области деформация ЖК совпадает с одномерной деформацией и соответствует центру электрода. Размер этой области для всех зависимостей определяется управляющим напряжением и с его ростом увеличивается. При малых управляющих напряжениях, которые не сильно превышают значения порогового напряжения размер этой области меньше, чем размер электрода, то есть в этом случае деформация ЖК, соответствующая одномерной деформации занимает область меньшую, чем сам электрод. С ростом управляющего напряжения размер первой области увеличивается и при высоких управляющих напряжениях, значительно превышающих пороговое значение, ее размер становится равным размеру электрода. Вторая область – это область где уже электрод отсутствует, но благодаря упругим свойствам ЖК ориентация молекул отлична от однородной. Это переходная область, в которой углы ориентации ЖК имеют промежуточное значение между значениями соответствующими углам ориентации недеформиро-ванного ЖК и углами ориентации, соответствующими деформации в центре электрода. Размер этой области также зависит от управляющего напряжения, но в меньшей степени. И третья область соответствует области недеформированного ЖК. Размер этой области уменьшается с ростом управляющего напряжения. Особый интерес вызывает вторая область с точки зрения поведения угла закрутки структуры ЖК, так как в ней эти изменения происходят наиболее резко, что может существенным образом влиять на оптические характеристики ЖК-устройств отображения информации, использующих различные электрооптические эффекты. Так, например, если устройство использует эффект управляемого двойного лучепреломления в различных структурах ЖК, то наличие второй области может существенным образом увеличить размер элемента изображения исказив его оптический отклик.

Если зафиксировать значение управляющего напряжения, при увеличении диэлектрической анизотропии размер первой области изменяется от 70 мкм до 80 мкм (размер электрода 90 мкм), а размер второй области остается постоянным и равным 30 мкм. Таким образом, если используется электрооптический эффект чувствительный в первую очередь к изменению только угла подъема молекул ЖК (например, эффект управляемого полем двойного лучепреломления в различных структурах ЖК), то элемент изображения может быть меньше, чем сам управляющий электрод, или по крайней мере иметь другие оптические характеристики. Аналогичные заключения можно сделать относительно влияния на размер элемента изображения отношений постоянных упругости ЖК, отличие только в размерах первой (80 мкм) и второй (40 мкм) областях, и которые слабо зависят от значения управляющего напряжения.

Максимальное влияние на двумерную деформацию ЖК в электрическом поле оказывает отношение размера электрода к толщине слоя ЖК, что согласуется с результатами работы [7]. В таблице приведены значения размеров первой и второй областей в зависимости от отношения L₁/d . Из этой таблицы видно, что при сравнимых значениях размера электрода и толщины ЖК – слоя отдельные элементы отображения перестают различаться, то есть выполнять свои функции. Однако, существует некоторое значение этого отношения, начиная с которого размер первой и второй области остаются постоянными. На рис. 2 и 3 представлены результаты вычислений влияния конструктивных параметров устройства (ширины электрода L₁ и величины межэлектродного расстояния d ) на его оптический отклик T (пропускание устройства). Как и в случае упругой деформации, с уменьшением отношения L 1 /d оптический отклик перестает отслеживать размер электрода и при сравнимых значениях ширины электрода и толщины ЖК-слоя возмущенной оказывается и область, где электрод отсутствует. При управляющих напряжениях близких к пороговому напряжению электрооптического эффекта оптический отклик устройства в зависимости от отношения L 1 /d в центре электрода различен (рис. 2), так как пороговое напряжение эффекта зависит от величины этого параметра.

Таблица.

Зависимость двумерной деформации ЖК в электрическом поле от отношения размера электрода к толщине слоя ЖК

L 1 /d	0.25	0.75	1.25	3.75	5	6.25	7.5	8.75
Размер первой области, мкм	20	50	60	80	90	90	90	90
Размер второй области, мкм	190	190	190	170	150	140	140	140

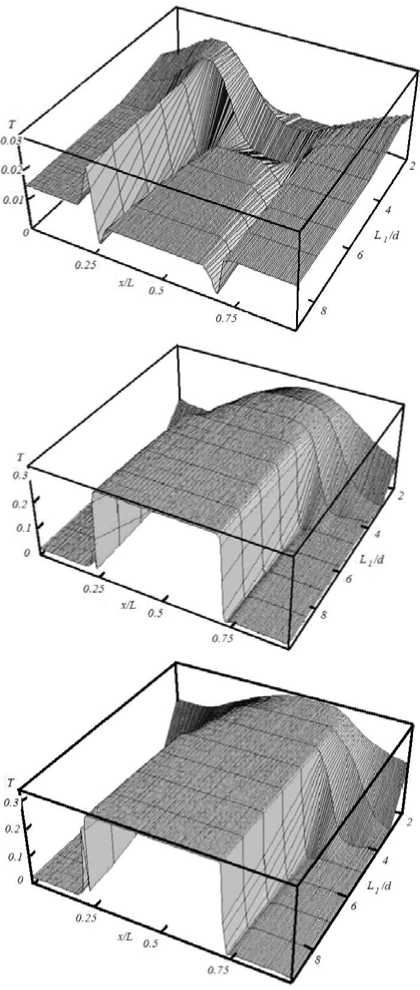
Рис. 2. Зависимость пропускания твист – индикатора от поперечной координаты и отношения толщины ЖК-ячейки к длине электрода для разных значений управляющего напряжения

А – V/V с =1,5; Б – V/V с =3,0; В – V/V с =5,0

Для высоких управляющих напряжений, значительно превышающих пороговое значение, оптический отклик индикатора в центре электрода не зависит от этого параметра. Кроме этого, как из рис. 3 видно, при одном и том же значении параметра L 1 /d=1 , но разных значениях толщины ЖК-слоя, оптический отклик устройства разный.

Это связано с большим влиянием на деформацию ЖК размера электрода и межэлектродного расстояния и в случае их малых величин слой ЖК оказывается сильно возмущенным не только в области электрода, но и в межэлектродном участке. Таким образом, в случае тонких ЖК-ячеек (d<4 мкм) размер электрода должен существенным образом превышать толщины ЖК-слоя, в то время как для толстых ЖК-ячеек (d>6 мкм) размер электрода может быть сравним с величиной d. С другой стороны, как и в случае упругой деформации, при низких управляющих напряжениях видимая величины элемента изображения на 50% меньше величины электрода, а при высоких значениях этого напряжения видимая величина элемента изображения на 16% больше, чем электрод. Это вызвано тем, что при управляющих напряжениях близких к пороговому, области ЖК, находящиеся вне электрода, стараются сохранять исходную ориентацию и в соседних с ними электродных областях, а так как управляющее напряжение мало, то и неискаженная область занимает часть электродной области. При больших управляющих напряжениях ситуация противоположна, и область находящаяся вне электрода становится искаженной, что приводит к видимому увеличению размера изображения.

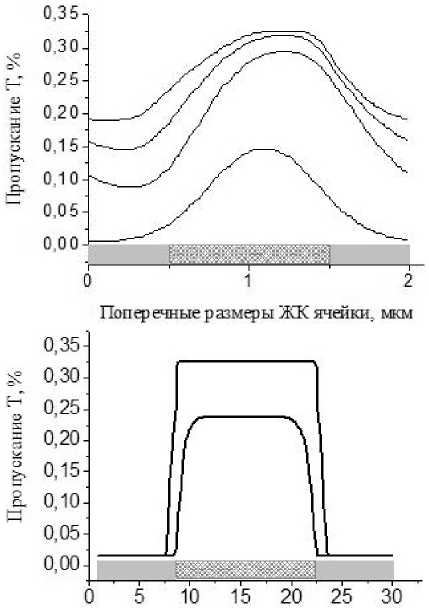
Поперечные размеры ЖК ячейки, мкм

Рис. 3. Зависимость пропускания твист-индикатора от поперечных размеров при различных толщины

ЖК-ячейки d и длины L₁ электрода А - d=L₁=1 мкм, V/Vc=2, 3, 4, 5; Б - d=L 1 =15 мкм, V/Vc=2,5

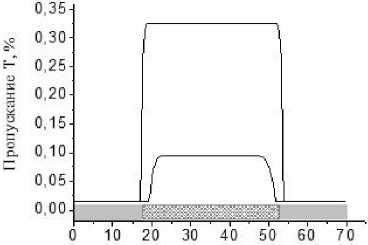
Физические параметры ЖК-устройства (отношение упругих постоянных K11/K33, K22/K33, диэлектрической анизотропии ∆ε) влияют на величину элемента изображения существенно меньшим образом, чем конструктивные параметры индикатора. На рис. 4 показано влияние величины диэлектрической анизотропии ЖК на размер изображения. При малых значениях ∆ε видимая величина элемента изображения и при малых управляющих напряжениях на 9% мень- ше, чем реальная величина электрода. При больших значениях напряжения размер изображения больше реального размера электрода на 5%. В то же время для большой диэлектрической анизотропии и при низких управляющих напряжений видимая величина элемента изображения меньше реального электрода на 5%, а при высоких управляющих напряжениях видимая величина элемента изображения на 5% больше электрода. Аналогичное поведение имеет зависимость видимого размера изображения от упругих постоянных ЖК. Отличие заключается в том, что при малых значениях отношения K22/K33 и при больших управляющих напряжениях видимая величина элемента изображения на 9% больше реального размера электрода, а при малых управляющих напряжениях видимый размер изображения совпадет с размером реального электрода.

Поперечные размеры ЖК ячейки, мкм

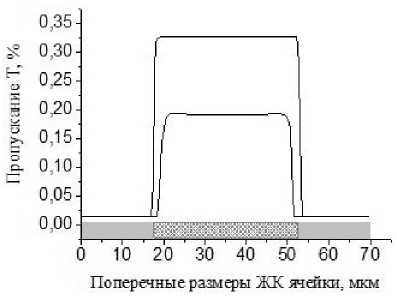
Рис. 4. Зависимость пропускания твист-индикатора от поперечных размеров при различных значениях диэлектрической анизотропии ЖК

А - Δε=7,8, V/Vc =2 и 5; Б - Δε =10, V/Vc=2 и 5

Заключение

Методом компьютерного моделирования выполнено исследование двумерной упругой деформации ЖК в электрическом поле и оптического отклика ЖК-устройства в зависимости от физических и конструктивных параметров ЖК-ячейки. Разработаны алгоритм и компьютерная программа для расчета двумерной упругой деформации ЖК в электрическом поле. Показано наличие различных областей деформации ЖК в случае двумерной деформации и выяснено влияние на размер этих областей физических и конструктивных параметров ЖК-ячейки.

Отмечено, что наибольшее влияние на размер областей двумерной деформации ЖК оказывает отношение величины электрода к величине толщины ЖК-слоя. Наибольшее влияние из физических параметров ЖК на его двумерную деформацию оказывает диэлектрическая анизотропия ЖК-материала. Аналогичные выводы можно сделать о влиянии этих параметров на кажущейся размер элемента отображения информации в твист-индикаторе.