Оптический сенсор поляризации на основе металинзы

Создание компактных быстродействующих оптических сенсоров для контроля за поляризацией света является актуальной задачей. Традиционные методы контроля поляризации света, такие как линейные поляризаторы, волновые пластинки, поляризационные модуляторы, как правило, не являются компактными и требуют нескольких измерений [1].

К компактным и быстрым оптическим сенсорам поляризации относятся поляризационно-изобража-ющие устройства [2], оптические [3] и плазмонные [4] поляриметры на чипе и хиральные делители пучка на гироидных фотонных кристаллах [5]. Но наиболее эффективные и компактные датчики поляризации создаются на основе метаповерхностей [6– 11]. Метаповерхности – наиболее универсальные оптические компоненты, так как позволяют манипулировать всеми световыми характеристиками (амплитудой, фазой и поляризацией) одновременно. Все рассмотренные метаповерхности [6– 11] работают по принципу пространственного разделения разных состояний поляризации. Например, в [6] метаповерхность из наностолбиков в виде параллелепипедов создана в пленке аморфного кремния толщиной 1680 нм. Длина столбиков –285 нм, ширина –55 нм и высота –1550 нм. Длина волны света – 974 нм. Поворотом столбиков контролируется задержка фазы. Метаповерхность работает как дифракционная решетка (период решетки –

• 3 мкм): левая круговая поляризация отклоняется в – 1 дифракционный порядок, правая круговая поляризация – в + 1 порядок, и линейная поляризация отклоняется в оба порядка – + 1 и – 1. Недостатком такого сенсора поляризации является высокий аспект наностолбиков (1550:55), отсутствие фокусирующей линзы и то, что для регистрации оптического сигнала требуются фотоприемники, разнесенные в пространстве.

В [7] изготовлен и исследован оптический элемент на основе диэлектрической градиентной метаповерхности, работающий как решетка с блеском (blazed grating) в слое кремния (Si) толщиной 100 нм на подложке из SiO2 для длины волны 550 нм. Решетка работает таким образом, что правая круговая поляризация идет в нулевой и – 1 дифракционный порядок, левая круговая поляризация идет в нулевой и + 1 порядки, а линейная поляризация идет в –1, 0 и +1 порядки. Причем в первый порядок идет примерно 35 % прошедшей решетку энергии (дифракционная эффективность). В [8] создали такую же градиентную метаповерхность в виде решетки с блеском, как в [7], но состоящую из золотых наностолбиков высотой 40 нм. Длина и ширина этих наностолбиков равна 200 нм и 50 нм. Изменение задержки фазы по поверхности решетки достигается за счет поворота наностолбиков. Период решетки равен 400 нм, рабочая длина волны – 633 нм. Решетка в [8] работает так же, как и решетка в [7]: правая круговая поляризация преобразуется метаповерхностью в левую круговую поляризацию и направляется в – 1 порядок. Левая круговая поляризация преобразуется в правую круговую поляризацию и направляется в + 1 порядок. А линейная поляризация разделяется метаповерхностью на левую круговую, которая идет в – 1 порядок, и на правую круговую поляризацию, которая идет в + 1 порядок. Период обеих решеток – около 3 мкм, поэтому порядки дифракции отклоняются от оптической оси примерно на 10 градусов. Поэтому пучки нулевого и первого порядков диаметром в десятки микрон разделятся в пространстве на расстоянии также десятков микрон после метарешетки. Отсутствие линзы у такого сенсора поляризаций увеличивает его размеры до сотни микрон. В [9] создана голограмма с метаповерхностью, состоящая из трех слоев: верхний слой – это набор наностолбиков из серебра (ширина – 75 нм, длина – 200 нм, высота – 30 нм), далее SiO2-разделитель (80 нм) и задний слой из серебра (150 нм) на кремниевой подложке. Размер метаатома – 450 × 450 нм, длина волны – 633 нм. При освещении метаголограммы излучением с левой круговой поляризацией в отраженном свете в + 1 порядке формируется изображение «пчелы», а в – 1 порядке – изображение «цветка». И, наоборот, при освещении метаголограммы излучением с правой круговой поляризацией в отраженном свете в +1 порядке формируется изображение «цветка», а в – 1 порядке – изображение «пчелы». При освещении мета голограммы светом с линейной поляризацией в + 1 и –1 порядках накладываются друг на друга оба изображения «пчелы» и «цветка». Недостатки этого датчика поляризации очевидны: работа на отражение увеличивает размеры датчика и требуется обработка изображений, чтобы отличить «пчелу» от «цветка». В [10] создана металинза для мультиспектрального хирального изображения, которая состоит из TiO2-«нанополоски» на подложке из стекла. Размеры «нанополосок»: длина – 250 нм, ширина – 80 нм и высота – 600 нм. Металинза работает почти для всего видимого диапазона длин волн (центральная длина волны – 550 нм), но при этом длина фокуса меняется от 22 мм (для длины волны 700 нм) до 34 мм (для длины волны 480 нм). При освещении такой металинзы излучением от осевого точечного источника с левой круговой поляризацией в плоскости изображения формируется изображение точки с одной стороны от оптической оси, а при освещении металинзы осевым точечным источником с правой круговой поляризацией изображение формируется с противоположной стороны от оптической оси. Такая металинза из-за большого фокусного расстояния (30 мм) не может служить прототипом микросенсора поляризации. В [11] создана метаповерхность на отражение, состоящая из наностолбиков из золота на SiO2-подложке. Каждый наностолбик расположен в ячейке размером 300×300 нм2. Длина волны – 650 нм. Данная метаповерхность предназначена для определения наклона большой оси эллипса поляризации к горизонтальной оси. Кроме отражающей метаповрехности, такой датчик поляризации должен иметь фокусирующий объектив и поляризатор-анализатор, кроме ССD. Так как у круговой поляризации обе оси эллипса поляризации одинаковые, то такой датчик не сможет отличить левую круговую поляризацию от правой.

В данной работе исследуется металинза, которая состоит из секторных бинарных субволновых решеток в пленке аморфного кремния. У данной металинзы отсутствуют недостатки, описанные выше: глубина рельефа металинзы всего 120 нм, металинза фокусирует излучения на расстоянии, равном длине волны (633 нм), и фотоприемники сосредоточены в области фокусного пятна. Такой сенсор поляризации работает следующим образом: левая круговая поляризация фокусируется в световое кольцо (в центре нулевая интенсивность), правая круговая поляризация формирует круглое фокусное пятно, и линейная поляризация формирует эллиптическое фокусное пятно с двумя боковыми лепестками.

Теоретические основания

Рассмотрим метаповерхность, которая в каждой точке поворачивает вектор поляризации падающего на нее лазерного света на угол, равный двойному полярному (азимутальному) углу 2φ, и реализует задержку фазы падающего излучения также пропорционально полярному углу. Матрица Джонса, описывающая пропускание такой металинзы, имеет вид:

-          , _ ( cos2 m- sin 2 ф

T ( ф ) = exp ( i ф ) 1 .         /

^ sin2 ф cos2 ф

Если метаповерхность (1) освещает свет с левой круговой поляризацией, то свет, прошедший через такую поверхность, будет по-прежнему иметь левую круговую поляризацию:

Exl

= T ( ф )

- i

, _ ( cos2 ф- sm2 фV 1 )          ( 1

= ^exP ( i ф ) 1 . _         „II . 1 = ^exP⁽ i З ф )| .

^ sin2 ф cos2 ф J^- i J          ^- i

где E x и E y – горизонтальная и вертикальная проекции поперечного вектора напряженности электрического поля. Если сфокусировать световое поле (2) идеальной сферической линзой с высокой числовой апертурой, то в плоскости фокуса сформируется световое кольцо. Действительно, в [12, 13] показано, что распределение интенсивности в остром фокусе света с начальной поперечной амплитудой вида

E x ] = A ( 9 ) e im ^ф ( 1   ]

Ey J       V2    [ i о J ,

где σ = 1 для правой круговой поляризации (RHCP), σ =– 1 для левой круговой поляризации (LHCP), σ =0

для линейно поляризованного излучения, и σ ≠ 0, ± 1 для эллиптической поляризации, A (θ) – угловой спектр начального поля, θ – угол зенита (два угла φ и θ задают точку на сфере), имеет вид:

I

^Г12m + 1 + I 2, m + 2 ) +

2^2 A

+Г( 2112m-I + 122mm-2 ) + COS 2^„ X

4 V

X( I0, mI2, m+2 + I0, mI 2, m-2   2 11, m-111, m+1 ) , где y± = (1 ± g) /2, и при о = 0 эти значения равны ( y+ =Y- = 1/ 72) и функции Iv,^ зависят только от радиальной переменной r в плоскости фокуса (z =0) и равны при любом z выражению:

I v»

f 4 пf ) ( X ^J

⁹ max

J sin ^{V+ 1}

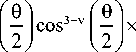
x cos1/2 (9) A (9) eiik cos6 Jц (x) d 9, где X - длина волны света; / - фокусное расстояния апланатической системы; x = krsin θ; Jμ (x) – функция Бесселя первого порядка; и NA = sin θmax – числовая апертура. Начальная функция амплитуды A(θ) (здесь предполагается, что она действительная) может быть константой (в случае плоской волны) или описывается функцией Гаусса. Для начального поля (2) в уравнении (4) следует выбрать m =3, γ+ =0, γ– = 1, σ2 = 1. Тогда выражение для распределения интенсивности в фокусе для начального поля (2) будет иметь вид:

1 3, - = 4 ( 1 02,3 + 2 1 122 + 1 22,1 ) .

Из (6) следует, что в центре фокуса (на оптической оси) при r =0 интенсивность равна нулю, так как второй индекс у функций I ν, μ равен номеру функции Бесселя, которая равна нулю при r =0, если номер μ≠ 0. Из (6) также следует, что картина интенсивности в фокусе имеет радиальную симметрию, так как интенсивность зависит только от радиальной переменной r . Таким образом, световое поле с левой круговой поляризацией с вектором Джонса (1,– i ) ^T , T – значок транспонирования, после прохождения через метаповерхность с пропусканием (1) преобразуется в оптический вихрь третьего порядка с левой круговой поляризацией (2). В остром фокусе такой световой пучок сформирует световое кольцо с нулевой интенсивностью в центре (6).

Если теперь метаповерхность (1) осветить светом с правой круговой поляризацией, то на выходе сформируется оптический вихрь минус первого порядка с правой круговой поляризацией:

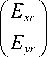
= T ( ф )

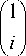
, _ f cos2 ф- sin2 ф^f 1 ^          f 1 )

= exp ( i ф ) 1 . ,         „ II . 1 = exp( - i ф )1 . I .

( Sin2 ф cos2 ф Д i J          ^ i J

Из уравнения (4) можно найти распределение интенсивности в остром фокусе для начального поля (7). Для этого положим в (4) m =– 1, γ + = 1, γ – =0, σ² = 1, тогда интенсивность в фокусе для начального поля (7) будет иметь вид:

I - 1, + = 4 ( 1 02,1 + 2 1 12o + 1 22,1 ) .                                (8)

В (8) второе слагаемое содержит функцию I 1,0 , у которой второй индекс равен нулю. Это означает, что в (5) под интегралом имеется функция Бесселя нулевого порядка, которая отлична от нуля при r =0. То есть в центре фокуса интенсивность будет иметь максимум и фокус будет иметь вид круглого светового пятна.

Если теперь метаповерхность (1) осветить светом с линейной поляризацией вдоль оси y , то на выходе сформируется оптический вихрь плюс первого порядка с азимутальной поляризацией второго порядка:

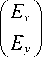
= T ( ф )

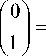
, _ f cos 2 ф - sin 2 ф1 f 0

= exp ( i ф ) 1                     II

^ sin2 ф cos2 ф J^ 1

f- sin 2 ф 1

= exp( i ф ) 1     „ I .

^ cos2 ф J

Найти интенсивность в фокусе для начального поля (9) уже нельзя с помощью выражения (4). В работе [12] получено общее выражение для интенсивности в фокусе для начального оптического вихря с топологическим зарядом m и азимутальной поляризацией порядка n с вектором Джонса вида:

E = A ( 9 ) e^{im ф}

- sin n ф

COS n ф

Распределение интенсивности для начального поля (10) в остром фокусе апланатической системы будет иметь вид:

2 (^J 0, m + n

22   2   2

0, m - n ⁺ I 2, m + n - 2 ⁺ I 2, m - n + 2 ) ⁺ I 1, m + n - 1 ⁺

1, m - n + 1 ⁺ (   1 )    ⁽ I 0, m + n I 2, m - n + 2 ⁺ I 0, m - n I 2, m + n - 2

-

- 2 1 ^m + n - 1 1 l, m - n + 1 ) X COS2 ( n - 1 ) ф.

Из (11) получим распределение интенсивности в фокусе для начального поля (9), положив в (11) m = 1, n = 2:

I = — ( I 02,3 ⁺ I 02,1 ^{+ 2} I 2,1 ) ⁺ 1 122 ⁺ 1 120 ^-

^- ( I 0,3 I 2,1 ^- I 0,1 1 2,1 ^{- 2} 1 1,2 1 1,0 ) ^{cos2 ф}.

Из (12) следует, что в центре фокуса на оптической оси (r =0) интенсивность не нулевая, так как в (12) имеется слагаемое I1,0, у которого второй индекс нулевой и поэтому под интегралом в (4) есть функция Бесселя нулевого порядка, которая при нулевом аргументе равна единице. Но фокусное пятно не будет обладать радиальной симметрией, так как в (12) имеется зависимость от полярного угла в виде cos2φ. В распределении интенсивности (12) будут, кроме центрального максимума, два дополнительных максимума (два боковых лепестка), лежащих на вертикальной оси при φ = π /2 и φ =3π /2. Так как при этих значениях угла cos2φ равен – 1, и вместо (12) получим выражение

I = 2 ( 1 0,3 + 1 2,1 ) 2 + 2 ( 1 0,1 - 1 2,1 ) 2 + ( 1 1,2 — 1 1,0 ) 2 . (13)

Заметим, что в [12, 13] получены общие уравнения для вихревого поля с топологическим зарядом m и с круговой поляризацией. В [13] показано, что при острой фокусировке обычного Гауссова пучка с круговой поляризацией в фокусе из-за спин-орбитального взаимодействия имеет место вращение поперечного потока энергии или, другими словами, появляется продольная компонента вектора орбитального углового момента. В данной работе на основе [12, 13] получены новые уравнения для описания в остром фокусе оптических вихрей с топологическим зарядом m =3 и правой круговой поляризацией (уравнения (6)), для оптического вихря с топологическим зарядом m =– 1 и левой круговой поляризацией (уравнение (8)), а также для оптического вихря с топологическим зарядом m = 1 и азимутальной поляризации второго порядка (уравнения (12) и (13)).

Итак, мы теоретически показали, что с помощью метаповерхности и фокусирующей линзы с высокой числовой апертурой можно легко детектировать различные состояния однородной поляризации лазерного пучка. Если на поверхность (1) падает свет с левой круговой поляризацией, то в фокусе сформируется световое кольцо с нулевой интенсивностью в центре. Если на поверхность (1) падает свет с правой круговой поляризацией, то в фокусе сформируется круглое световое пятно с максимумом в центре. И если на поверхность (1) падает свет с линейной поляризацией, то в фокусе сформируется эллиптическое фокусное пятно с двумя боковыми лепестками. Причем отрезок, соединяющий центры двух боковых лепестков, будет показывать направление вектора линейной поляризации начального светового поля. Численное моделирование, проведенное в следующем параграфе, подтверждает теоретические выводы.

Моделирование

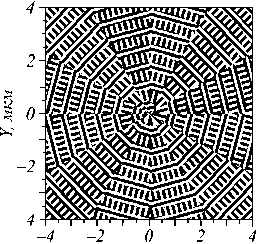
В этом параграфе мы рассчитаем металинзу, состоящую из секторных субволновых решеток, функция пропускания которых описывается матрицей в уравнении (1) и спиральной бинарной зонной пластинкой с высокой числовой апертурой. Спиральная зонная пластинка первого порядка (рис. 1б) выполня- ет две функции: формирует из падающего на нее излучения оптический вихрь с топологическим зарядом + 1 и фокусирует свет, прошедший через нее. Зонная пластинка должна иметь высокую числовую апертуру (близкую к единице), чтобы три амплитуды начальных световых полей (2), (7) и (9) сформировали в остром фокусе из-за спин-орбитальной конверсии разные фокусные пятна. На рис. 1а показана рассматриваемая металинза. Ее параметры: длина волны света λ =633 нм, фокусное расстояние металинзы f = λ, материал металинзы – аморфный кремний (показатель преломления n = 4,33 + 0,486i), высота рельефа – 120 нм. Металинза сформирована из секторных бинарных субволновых дифракционных решеток (период – 220 нм), ширина канавки которых составляет 110 нм, ширина ступеньки – 110 нм. Падающее световое поле ограничено круглой апертурой с радиусом 4 мкм. Небольшой размер металинзы выбран для удобства расчетов. Подробное описание формирования таких секторных металинз можно найти в работе [14]. На рис. 1б показан шаблон бинарной спиральной зонной пластинки, которая входит в состав металинзы на рис. 1a.

Маска металинзы

• а)

Спиральная зонная пластинка

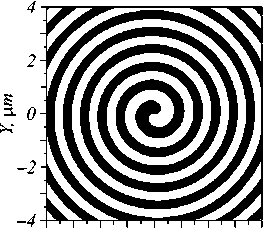
-4-2   0   2   4

• б)

Рис. 1. Вид рассматриваемой металинзы, размер изображения – 8×8 μm (a), и фазовая спиральная зонная пластинка, включенная в металинзу (б)

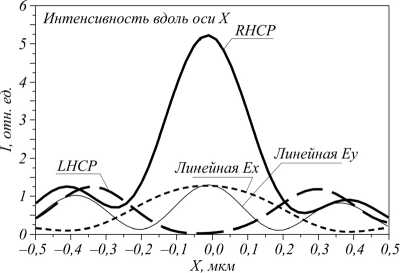
Моделирование проводилось при помощи решения уравнения Максвелла с помощью метода конечных разностей во временной области (FDTD), реализованного в программном пакете FullWave (Rsoft). Сетка разбиения вдоль всех трех координат была взята λ /30. На рис. 2 показаны интенсивности лазерных пучков с четырьмя видами поляризации – левой кру- говой (LHCP), правой круговой (RHCP), линейной поляризацией с вектором электрического поля вдоль Падающая - LHCP

а)

в)

а)

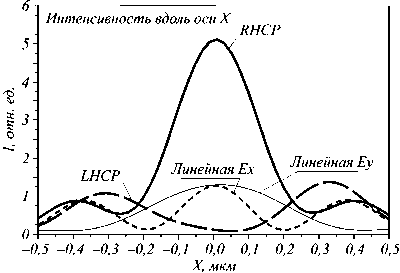
Рис. 3. Сечения распределений интенсивности вдоль осей X (а) и Y (б) для всех видов поляризаций падающего пучка

б)

Как видно из рис. 2 и 3, все четыре поляризации формируют разные фокусные пятна как по форме, так и по амплитуде. Правая круговая поляризация формирует круглое фокусное пятно (рис. 2 б ) с диаметром по полуспаду интенсивности FWHM=0,427λ. Левая круговая поляризация формирует в фокусе металинзы (рис. 1) световое кольцо с радиусом 0,31 мкм и шириной кольца 0,4λ. При фокусировке линейной поляризации получается эллиптическое фокусное пятно с шириной по полуспаду интенсивности FWHM=0,32λ вдоль малой оси эллипса и FWHM=0,68λ вдоль большой оси эллипса.

Располагая один или два датчика интенсивности в фокусной плоскости, можно детектировать поляризацию пучка. В качестве датчиков можно использовать как ПЗС-матрицу, так и специально изготовленные датчики с предустановленным расположением всего осей X и Y, после прохождения металинзы (рис. 1).

На рис. 3 – их сечения вдоль осей X и Y.

Падающая - RHCP

Рис. 2. Распределение интенсивности в фокусе металинзы (рис. 1) для четырех различных типов поляризации падающего пучка: LHCP (a), RHCP (б), линейная Ex (в), линейная Ey (г)

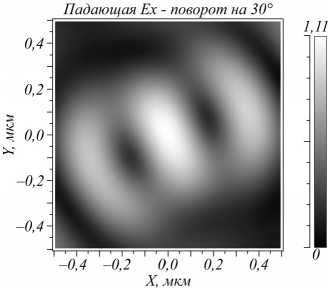
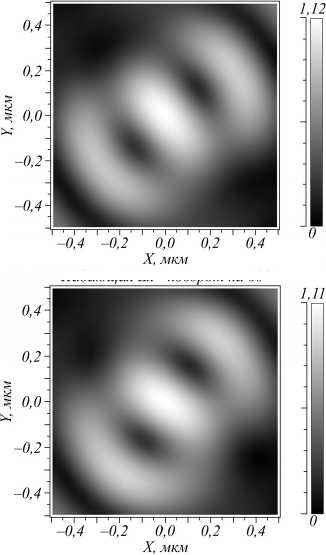
нескольких чувствительных элементов на них, что при серийном изготовлении может снизить цену на них ниже стоимости ПЗС-матриц. Например, измеряя только интенсивность фокусного пятна в центре, можно однозначно определить 3 вида поляризации: LHCP, RHCP, линейную Ex или Ey. Для того, чтобы определить тип линейной поляризации, потребуется еще один датчик, расположенный по оси X или Y на расстоянии 0,38 мкм от центра. Из рис. 2 видно, что в случае линейной поляризации в фокусной плоскости формируется эллиптическое фокусное пятно с боковыми лепестками, при повороте вектора электрического падающего поля оно поворачивается вокруг своей оси так, что боковые лепестки находятся вдоль оси колебания электрического вектора начального поля. Это продемонстрировано на рис. 4. Таким образом, при произвольной линейной поляризации можно определить ее ориентацию, если на том же радиусе 0,38 мкм расположить достаточное количество датчиков интенсивности.

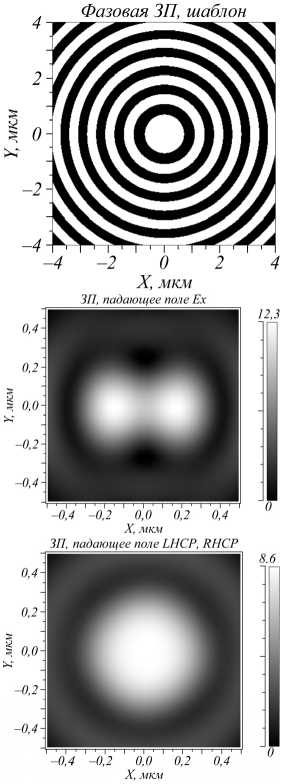
Для полноты картины ниже приводится фокусировка света с разной поляризацией с помощью бинарной зонной пластинки с такой же числовой апертурой, как у металинзы ( NA = 0,9877). На рис. 5 a показан бинарный шаблон зонной пластинки (черные кольца – фаза π, белые кольца – фаза ноль). На рис. 5 б показано фокусное пятно в виде гантели для света с линейной поляризацией вдоль оси X, а на рис. 5 в показано круглое фокусное пятно для левой и правой круговой поляризации. Из рис. 5 видно, что отличить левую поляризацию от правой в фокусе обычной ЗП нельзя.

а)

Падающая Ex - поворот на 45'

б)

в)

Рис. 4. Распределение интенсивности в фокальной плоскости для различных поворотов φ вектора электрического поля линейной поляризации падающего пучка: 30° (a), 45° (б), 60° (в)

Падающая Ех - поворот на 601

Из сравнения рис. 2б и рис. 5б следует интересный эффект: диаметр фокуса света с круговой поляризацией равен FWHM=0,826λ (рис. 5б) и примерно в 2 раза больше, чем диаметр фокуса для оптического вихря с топологическим зарядом -1 и правой круговой поляризацией (FWHM=0,427λ) (рис. 2б) при одинаковой числовой апертуре 1. Так получается потому, что фокус на рис. 2б формируется в основном с помощью продольной составляющей электрического поля Ez, а на рис. 5б продольная составляющая имеет вид кольца и уширяет фокусное пятно.

а)

б)

в)

Рис. 5. Шаблон фазовой бинарной зонной пластинки (a) и распределение интенсивности в фокусной плоскости (на расстоянии f = λ = 633 мкм) для света с линейной поляризацией вдоль оси X (б) и с круговой (левой и правой) поляризацией (в)

Заключение

В работе теоретически и численно исследовалось устройство для детектирования поляризации на основе металинзы в тонкой пленке кремния с высокой числовой апертурой. Известные аналогичные датчики поляризации на основе металинз [6–8] не включают в себя фокусирующую линзу и отклоняют свет с разной поляризацией на разные углы. Это приводит к увеличению габаритов датчика и к необходимости использовать матрицу фотоприемников (CCD-камеру). Рассмотренный в работе датчик поляризации имеет размеры всего десятки микрон, фокусирует свет на расстоянии длины волны и основан на другом принципе. Данный датчик не отклоняет свет разной поляризации на разные углы, а формирует в фокусе на оптической оси разные картины дифракции (фокусное круглое пятно, световое кольцо и эллиптическое фокусное пятно с боковыми лепестками). Это позволяет заменить матрицу фотоприемников на один или два одиночных фотоприемника с чувствительной площадкой в несколько сотен нанометров. Рассмотренный в работе датчик поляризации найдет применение в задачах контроля состояния поляризации в биологии [15], медицине [16, 17], микроскопии [18, 19].

Работа выполнена при поддержке Российского научного фонда (грант 22-22-00265).